Understanding Investment Performance Beyond Simple Returns
Evaluating investment performance solely on raw returns provides an incomplete picture. Raw returns don’t account for the risk taken to achieve those returns. A portfolio might generate high returns, but if it involved exceptionally high risk, those returns might not be truly impressive. Investors need a method to compare portfolios with different risk profiles. Risk-adjusted return measures help achieve this comparison. Understanding risk-adjusted return is crucial for making informed decisions. The Sharpe ratio is a key tool for evaluating risk-adjusted return. The Sharpe ratio of a portfolio is a widely used metric in finance. It allows investors to assess the excess return generated per unit of risk. A higher Sharpe ratio generally suggests better risk-adjusted performance. However, remember that the Sharpe ratio of a portfolio is not the only factor to consider. Other metrics provide additional insights into performance.
The limitations of relying solely on raw returns are significant. Two portfolios may show similar returns, yet their risk profiles can differ greatly. One might have achieved those returns through aggressive strategies, while the other employed a more conservative approach. Comparing them based on returns alone ignores this vital difference. Investors must look beyond the headline numbers to gauge the true performance of their investments. Analyzing risk alongside return helps determine whether the returns justify the risk taken. This is where the concept of risk-adjusted return becomes critical. The Sharpe ratio of a portfolio is a valuable tool that helps quantify this risk-adjusted return. It provides a standardized measure, allowing for easier comparisons across different portfolios with varied risk levels. Understanding this ratio’s calculation and interpretation is paramount to effective investment management. The Sharpe ratio of a portfolio is essential for making informed choices.
Many investors focus primarily on maximizing returns. However, ignoring risk is a serious oversight. High returns accompanied by excessive risk may lead to substantial losses. Conversely, lower returns coupled with significantly lower risk can provide a more stable and reliable investment experience. The Sharpe ratio helps investors strike the optimal balance between risk and return. By considering both factors, investors can make better-informed decisions about their portfolios. The Sharpe ratio of a portfolio is a crucial metric for optimizing this balance, promoting more successful investment strategies. Investors should avoid making investment decisions solely based on a high return without understanding its associated risk.
What is the Sharpe Ratio and Why Does It Matter?
The Sharpe Ratio is a crucial metric in finance. It quantifies the risk-adjusted return of an investment. In simpler terms, it measures excess return per unit of risk. The Sharpe Ratio of a portfolio is calculated by subtracting the risk-free rate of return from the portfolio’s return, and then dividing the result by the portfolio’s standard deviation. A higher Sharpe Ratio generally suggests better risk-adjusted performance. The Sharpe Ratio of a portfolio is a valuable tool for comparing investments with different levels of risk.
The formula for calculating the Sharpe Ratio is: (Rp – Rf) / σp, where Rp represents the portfolio return, Rf represents the risk-free rate of return, and σp represents the portfolio’s standard deviation (a measure of volatility or risk). For example, imagine Portfolio A has a return of 15%, a standard deviation of 10%, and the risk-free rate is 3%. Its Sharpe Ratio would be (0.15 – 0.03) / 0.10 = 1.2. Portfolio B, with a return of 20% and a standard deviation of 20%, would have a Sharpe Ratio of (0.20 – 0.03) / 0.20 = 0.85. Despite having a higher return, Portfolio A exhibits better risk-adjusted performance, as indicated by its higher Sharpe Ratio. The Sharpe Ratio of a portfolio is a key factor for investors.
Understanding the Sharpe Ratio is essential for informed investment decisions. It provides a standardized way to compare the performance of different portfolios, regardless of their risk profiles. Investors can use the Sharpe Ratio to identify portfolios that deliver higher returns relative to their risk. The Sharpe Ratio of a portfolio is not a standalone indicator, but it is a powerful tool for comparing investment opportunities. It helps investors make decisions aligned with their risk tolerance and return expectations.
Dissecting the Components: Return and Risk
The Sharpe Ratio of a portfolio is a crucial metric for evaluating investment performance. It elegantly combines two fundamental aspects: portfolio return and portfolio risk. Understanding these components is vital for interpreting the Sharpe Ratio effectively. Portfolio return represents the overall profit or loss generated by an investment over a specific period. It’s typically expressed as a percentage and calculated by subtracting the initial investment from the final value, then dividing by the initial investment. A higher portfolio return, all else being equal, contributes to a better Sharpe Ratio. The calculation is straightforward, yet its impact on the Sharpe Ratio of a portfolio is significant.
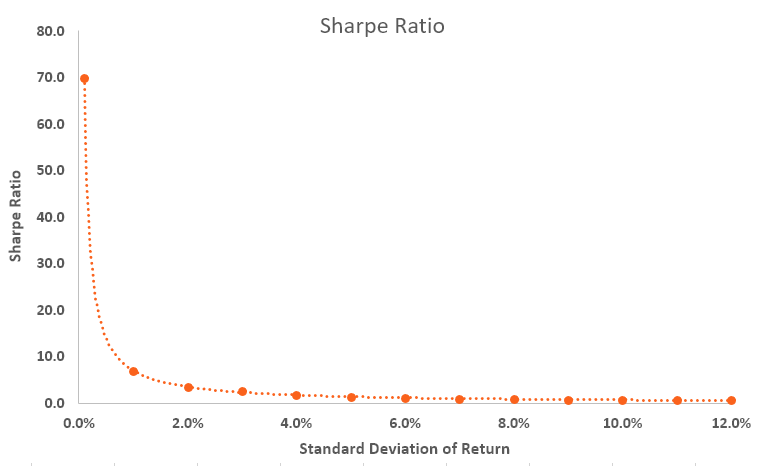
Portfolio risk, on the other hand, quantifies the volatility or uncertainty associated with the investment’s returns. It’s most commonly measured using standard deviation. Standard deviation calculates the average dispersion of returns around the mean return. A higher standard deviation indicates greater risk; returns fluctuate more widely around the average. The Sharpe Ratio of a portfolio is significantly influenced by this risk factor. Lower standard deviation suggests less risk, which improves the Sharpe Ratio. The impact of both higher returns and lower risk on the Sharpe Ratio is multiplicative; the benefit of higher returns is amplified when the accompanying risk is low. This means the sharpe ratio of a portfolio is effectively elevated by both factors simultaneously.
Consider two hypothetical portfolios. Portfolio A boasts an average annual return of 15% but has a standard deviation of 10%. Portfolio B, conversely, generates an average annual return of 12% but possesses a standard deviation of only 5%. While Portfolio A boasts a higher return, the greater risk may result in a lower Sharpe Ratio compared to Portfolio B. This illustrates the importance of considering both return and risk when evaluating investment performance. The Sharpe Ratio of a portfolio is not simply about chasing high returns; it’s about achieving those returns relative to the risk undertaken. Understanding the interplay of return and risk is essential for accurately interpreting and utilizing the Sharpe Ratio.
How to Calculate the Sharpe Ratio for Your Portfolio
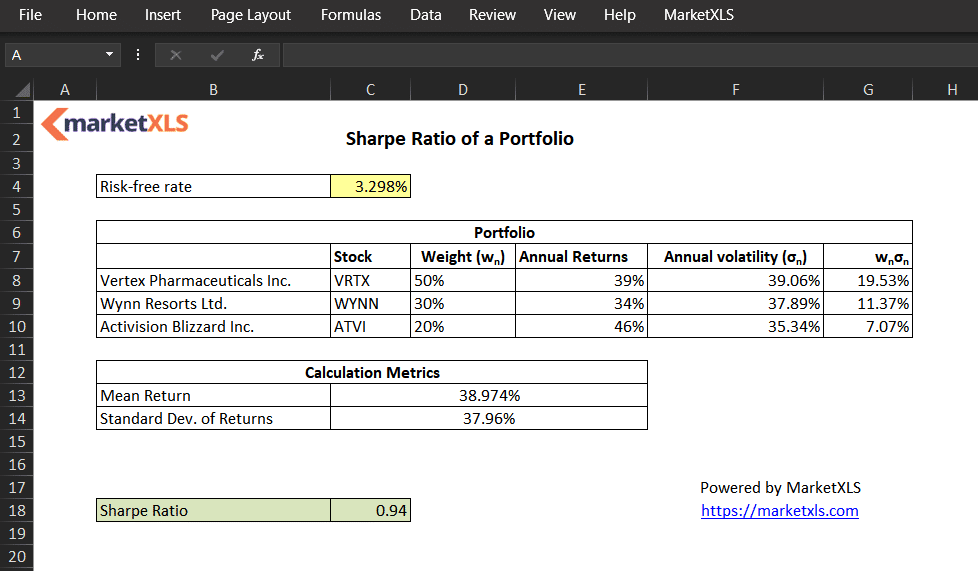
Calculating the Sharpe Ratio of a portfolio is a straightforward process, requiring readily available data. The formula is: Sharpe Ratio = (Rp – Rf) / σp, where Rp represents the portfolio return, Rf denotes the risk-free rate of return, and σp signifies the portfolio’s standard deviation. To determine the Sharpe Ratio of a portfolio, one must first calculate the portfolio return and standard deviation. The portfolio return is the average return of the portfolio over a specified period. This is found by summing the individual returns for each period and dividing by the number of periods. For instance, if a portfolio returned 10%, 12%, and 8% over three months, the average monthly return would be (10% + 12% + 8%) / 3 = 10%. Next, the standard deviation, representing the portfolio’s volatility, is calculated using the historical return data. This measures the dispersion of returns around the average. The calculation involves finding the variance (the average of the squared differences from the mean) and taking its square root to get the standard deviation. The risk-free rate of return, typically the yield on a government bond, is subtracted from the average portfolio return. The result is then divided by the standard deviation of the portfolio. This yields the Sharpe Ratio. The Sharpe Ratio of a portfolio is a crucial indicator of risk-adjusted return.
Let’s illustrate with a hypothetical example. Suppose a portfolio has an average monthly return (Rp) of 10%, and the standard deviation (σp) of its monthly returns is 5%. If the risk-free rate (Rf) is 2% (e.g., a government bond yield), the Sharpe Ratio calculation is: (0.10 – 0.02) / 0.05 = 1.6. This indicates a Sharpe Ratio of 1.6. Remember, the Sharpe Ratio of a portfolio is a relative measure. A higher Sharpe Ratio suggests superior risk-adjusted performance. The calculation process for the Sharpe ratio of a portfolio remains consistent regardless of the investment asset class. However, selecting the appropriate risk-free rate is critical. Using a longer time period for the calculation generally results in more reliable results. Accessing historical portfolio returns and risk-free rate data usually involves consulting financial databases or brokerage statements. The Sharpe ratio of a portfolio is easily calculated using readily available financial software or spreadsheets.
Organizing the calculations in a table simplifies the process. A table might include columns for the period, portfolio return for each period, deviations from the average return, squared deviations, and finally the calculation of variance and standard deviation. This systematic approach helps avoid calculation errors and allows for a clear understanding of each step in determining the Sharpe ratio of a portfolio. It’s important to note that the Sharpe ratio of a portfolio is not a standalone metric for investment decisions. It is most useful when comparing different portfolios or investment strategies. The Sharpe ratio of a portfolio should be considered in conjunction with other metrics and qualitative factors for a complete assessment of investment performance. Understanding how to calculate and interpret the Sharpe ratio of a portfolio is a valuable skill for any investor.
Interpreting the Sharpe Ratio: What Do the Numbers Mean?
Interpreting the Sharpe Ratio involves understanding that a higher value generally signifies better risk-adjusted performance. A Sharpe Ratio above 1 is often considered acceptable to many investors. A ratio above 2 is very good, while a ratio above 3 is excellent. However, these are broad guidelines. The Sharpe ratio of a portfolio is highly context-dependent. Factors such as the investment’s asset class and the investor’s risk tolerance significantly influence the interpretation. For example, a high-growth equity portfolio might be expected to have a lower Sharpe ratio than a bond portfolio, even if both perform well. The Sharpe ratio of a portfolio is not a standalone metric; it’s most useful when comparing similar investment strategies or asset classes.
It’s crucial to remember that the Sharpe Ratio of a portfolio is just one piece of the puzzle. A high Sharpe Ratio doesn’t guarantee future success. Past performance is not indicative of future results. Market conditions can change, affecting the performance of even the best-performing portfolios. The calculation relies on historical data, which may not accurately predict future returns or volatility. Furthermore, the choice of the risk-free rate significantly impacts the final result. A longer time period usually provides a more stable and reliable Sharpe Ratio, but even then, it has limitations. A low Sharpe ratio might indicate the portfolio underperformed considering the risk taken. Conversely, a portfolio with a seemingly high Sharpe ratio may involve hidden risks or strategies that won’t be sustainable.
Therefore, investors should carefully analyze the Sharpe ratio of a portfolio within the larger context of their investment goals, risk tolerance, and overall portfolio strategy. It is vital to consider the limitations. Comparing the Sharpe Ratio to other performance metrics offers a more complete picture. Relying solely on this one metric can be misleading. The Sharpe ratio of a portfolio is a valuable tool, but it should not be used in isolation. Investors should always incorporate other analytical tools and qualitative factors into their investment decision-making process. Understanding the nuances of this ratio and its limitations is paramount for making informed and responsible investment choices.
Sharpe Ratio vs. Other Performance Metrics: A Comparison
The Sharpe ratio, while a widely used metric, isn’t the only tool for evaluating investment performance. Other ratios offer different perspectives on risk-adjusted returns. The Sortino ratio, for instance, focuses solely on downside risk, penalizing negative deviations from the mean more heavily than the Sharpe ratio. This makes it particularly useful for investors with risk-averse profiles or strategies aimed at minimizing losses. The Sortino ratio is calculated by dividing the excess return by the downside deviation. Understanding the nuances of the Sortino ratio is crucial, as it provides a more refined analysis than the Sharpe ratio in specific circumstances. The Sharpe ratio of a portfolio is often compared to the Sortino ratio to gain a clearer picture of risk-adjusted performance.
Another key metric is the Treynor ratio, which measures the excess return per unit of systematic risk (beta). Unlike the Sharpe ratio, which considers total risk, the Treynor ratio focuses on market risk. This makes it particularly relevant for diversified portfolios where unsystematic risk is largely diversified away. Investors looking to assess the contribution of a portfolio to the overall market risk should find the Treynor ratio more informative than the Sharpe ratio. The Treynor ratio of a well-diversified portfolio is often more revealing than the Sharpe ratio in instances where market risk is a more significant factor compared to total risk. The Sharpe ratio of a portfolio is not always the best metric when considering systematic risk alone.
Choosing between the Sharpe, Sortino, and Treynor ratios depends on the investment strategy and risk profile. For example, a conservative investor might prefer the Sortino ratio, while an investor focused on market-timing might find the Treynor ratio more relevant. The Sharpe ratio remains a widely understood and useful benchmark, but its limitations should be acknowledged. Investors should consider using a combination of these metrics, alongside qualitative analysis, to make comprehensive and informed investment decisions. The Sharpe ratio of a portfolio is just one piece of the puzzle. Using it in conjunction with other metrics allows for a holistic evaluation of investment performance.
Using the Sharpe Ratio to Make Informed Investment Decisions
Investors can leverage the Sharpe ratio to compare the risk-adjusted returns of different investment options. By calculating the Sharpe ratio of a portfolio is essential for making informed decisions. A higher Sharpe ratio suggests superior risk-adjusted performance, indicating a better return relative to the risk taken. This allows for a more effective comparison between investments with differing risk profiles, facilitating a more objective selection process. Understanding the Sharpe ratio of a portfolio is crucial for optimizing portfolio allocation, leading to more efficient risk management and potentially higher returns. The Sharpe ratio of a portfolio is a key metric for evaluating investment choices.
The Sharpe ratio aids in portfolio allocation. Investors can use it to strategically distribute assets across various investment options. For example, an investor may decide to allocate more capital to investments with higher Sharpe ratios, provided that these align with the investor’s risk tolerance. Regularly monitoring the Sharpe ratio of a portfolio is essential for assessing the ongoing performance of the portfolio and identifying potential areas for adjustment. This dynamic approach ensures the portfolio maintains its desired risk-adjusted return profile over time. The Sharpe ratio of a portfolio is a valuable tool in this continuous monitoring and adjustment process.
Incorporating the Sharpe ratio into an overall investment strategy requires a balanced approach. While the Sharpe ratio provides valuable insights into risk-adjusted returns, it shouldn’t be the sole factor in investment decisions. Qualitative factors, such as the investor’s risk tolerance, investment timeline, and overall financial goals, must also be considered. The Sharpe ratio of a portfolio is one piece of the puzzle; combining it with a thorough understanding of individual investment objectives enables a more comprehensive and robust investment strategy. Remember that the Sharpe ratio of a portfolio is just one metric; a holistic approach leads to more informed decisions. The calculation of the Sharpe ratio of a portfolio is a straightforward process.
Beyond the Numbers: Practical Considerations and Limitations
While the Sharpe ratio offers a valuable tool for evaluating portfolio performance, it’s crucial to acknowledge its limitations. The accuracy of the Sharpe ratio of a portfolio is heavily reliant on the quality and length of the historical data used in its calculation. Insufficient data or data skewed by unusual market events can distort the results, leading to inaccurate conclusions. Similarly, the choice of the risk-free rate significantly influences the final Sharpe ratio. Different risk-free rates, such as those based on government bonds with varying maturities, will produce different results. The Sharpe ratio of a portfolio is not a static measure; it fluctuates over time reflecting changes in market conditions and portfolio composition. Therefore, investors should analyze the ratio across multiple periods to gain a more comprehensive understanding of long-term performance.
Furthermore, the Sharpe ratio assumes a normal distribution of returns. However, investment returns, particularly in certain asset classes, often exhibit deviations from normality, such as skewness and kurtosis. These deviations can undermine the accuracy of the Sharpe ratio in capturing true risk-adjusted performance. The calculation of the Sharpe ratio of a portfolio also simplifies risk to standard deviation, neglecting other aspects of risk like downside risk or tail risk. This means the Sharpe ratio might not fully capture the potential for extreme losses. For instance, two portfolios might have similar Sharpe ratios, but one might have experienced significant drawdowns that the standard deviation doesn’t fully reflect.
Therefore, relying solely on the Sharpe ratio of a portfolio is unwise. It serves as a valuable tool when used in conjunction with other performance metrics, qualitative assessments, and a thorough understanding of the investment strategy and market conditions. Investors should consider the specific characteristics of the portfolio, its investment goals, and risk tolerance. The Sharpe ratio provides one piece of the puzzle. Investors need to consider a broader picture for comprehensive investment decision-making. Remember, the Sharpe ratio of a portfolio is just one metric; a balanced approach integrating multiple analyses ensures a more robust evaluation of investment performance.