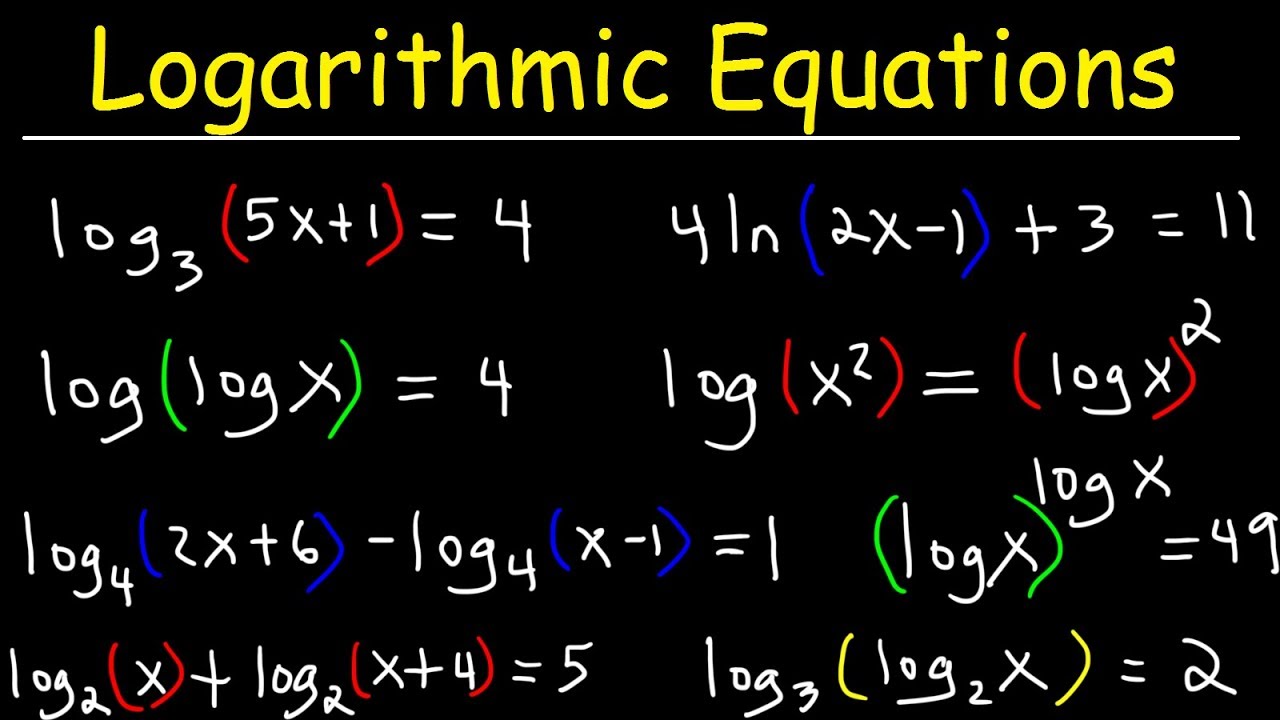What is a Logarithm and Why is it Important?
In the realm of mathematics, logarithms play a vital role in simplifying complex calculations and solving real-world problems. A logarithm is the inverse operation of exponentiation, where a base number is raised to a power to produce a given value. In essence, logarithms help us find the power to which a base number must be raised to equal a specified value. Understanding how to calculate a logarithm is crucial in various fields, including science, engineering, economics, and computer science, as it enables us to model and analyze complex phenomena, make predictions, and optimize systems. By grasping the concept of logarithms, individuals can unlock the power to tackle complex problems and make informed decisions in their respective fields.
Understanding the Different Types of Logarithms
Logarithms come in various forms, each with its unique characteristics and applications. The most common types of logarithms are natural logarithms, common logarithms, and logarithms with different bases. Natural logarithms, denoted by ln(x), have a base of Euler’s number (e), approximately 2.718. They are used extensively in mathematics, particularly in calculus and exponential functions. Common logarithms, denoted by log(x), have a base of 10 and are commonly used in everyday applications, such as calculating the magnitude of earthquakes or the pH of a solution. Logarithms with different bases, denoted by logb(x), can have any positive real number as their base. Understanding the differences between these types of logarithms is essential to accurately applying them in various mathematical and real-world contexts. By recognizing the unique properties of each type, individuals can effectively choose the right logarithm to tackle complex problems and make informed decisions.
How to Calculate a Logarithm: The Basics
Calculating a logarithm involves understanding the fundamental formula and notation. The basic formula for a logarithm is logb(x) = y, where b is the base, x is the argument, and y is the exponent. To calculate a logarithm, one needs to find the power to which the base must be raised to equal the argument. For instance, to calculate log2(8), we need to find the power to which 2 must be raised to equal 8, which is 3, since 2^3 = 8. When learning how to calculate a logarithm, it is essential to understand the notation and the formula to avoid confusion. Simple examples, such as calculating log10(100) or ln(e), can help illustrate the process and build a strong foundation for more complex calculations. By grasping the basics of logarithmic calculations, individuals can develop a deeper understanding of mathematical concepts and improve their problem-solving skills.
Using Logarithmic Tables and Calculators
In the past, logarithmic tables were a crucial tool for simplifying complex logarithmic calculations. These tables provided pre-calculated logarithmic values for various bases, allowing individuals to quickly look up the logarithm of a number. Although logarithmic tables are still useful, calculators have largely replaced them as the primary tool for logarithmic calculations. Calculators can instantly calculate logarithms with high accuracy, making them an essential tool for students, professionals, and anyone needing to perform logarithmic calculations. However, it is essential to understand how to use calculators correctly to avoid errors. For instance, when using a calculator to calculate a logarithm, it is crucial to ensure that the correct base is selected. Additionally, understanding how to calculate a logarithm manually is still important, as it provides a deeper understanding of the underlying mathematical concepts. By combining the use of logarithmic tables and calculators with a solid understanding of how to calculate a logarithm, individuals can efficiently and accurately perform complex calculations.
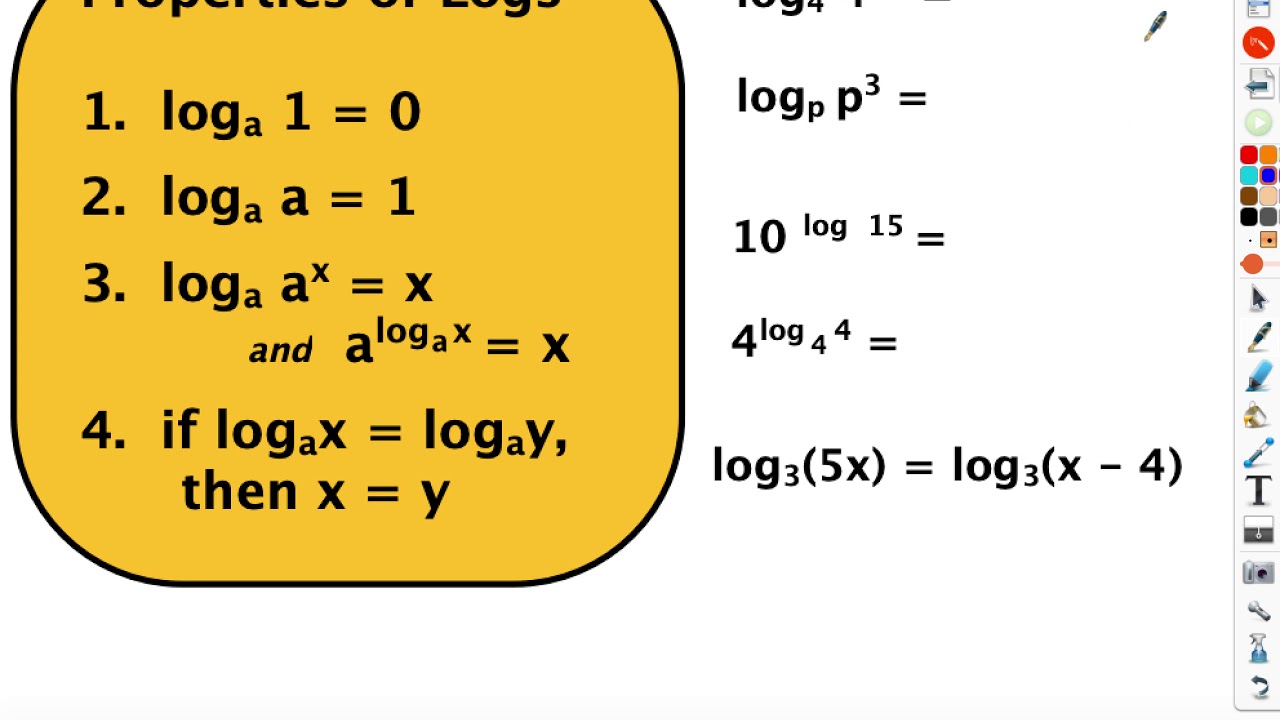
Logarithmic Identities and Rules
Mastering logarithmic identities and rules is essential for simplifying complex calculations and solving problems efficiently. One of the most important logarithmic identities is the product rule, which states that logb(xy) = logb(x) + logb(y). This rule allows individuals to break down complex logarithmic expressions into simpler components. Another crucial identity is the quotient rule, which states that logb(x/y) = logb(x) – logb(y). This rule is particularly useful when dealing with fractions or ratios. The power rule, which states that logb(x^n) = n \* logb(x), is also a powerful tool for simplifying logarithmic expressions. By applying these identities and rules, individuals can simplify complex calculations and develop a deeper understanding of logarithmic concepts. For instance, using the product rule, one can simplify the expression log2(8 \* 16) by breaking it down into log2(8) + log2(16). By mastering these logarithmic identities and rules, individuals can improve their problem-solving skills and become proficient in how to calculate a logarithm.
Real-World Applications of Logarithms
Logarithms have numerous practical applications in various fields, making them an essential tool for problem-solving and critical thinking. In science, logarithms are used to model population growth, chemical reactions, and sound waves. For instance, the pH level of a solution is calculated using the logarithm of the hydrogen ion concentration. In engineering, logarithms are used to design electronic circuits, calculate signal amplification, and optimize system performance. In economics, logarithms are used to model economic growth, inflation rates, and investment returns. In computer science, logarithms are used in algorithms for data compression, encryption, and search engine optimization. Understanding how to calculate a logarithm is crucial in these fields, as it enables individuals to analyze and interpret complex data, make informed decisions, and drive innovation. For example, in finance, logarithmic calculations can help investors determine the optimal investment strategy based on risk and return. By recognizing the significance of logarithms in real-world applications, individuals can appreciate the importance of mastering logarithmic calculations and develop a deeper understanding of how to calculate a logarithm.
Common Mistakes to Avoid When Calculating Logarithms
When learning how to calculate a logarithm, it’s essential to be aware of common mistakes and pitfalls that can lead to inaccurate results. One common error is forgetting to change the base of the logarithm when switching between different types of logarithms. For instance, when converting from natural logarithms to common logarithms, individuals must remember to adjust the base accordingly. Another mistake is neglecting to follow the order of operations when calculating logarithms, leading to incorrect calculations. Additionally, individuals may mistakenly apply logarithmic identities and rules without fully understanding their applications, resulting in incorrect simplifications. Furthermore, failing to check the domain and range of the logarithmic function can lead to errors in calculation. To avoid these mistakes, it’s crucial to develop a solid understanding of logarithmic concepts, practice regularly, and double-check calculations. By being mindful of these common errors, individuals can improve their accuracy and confidence when learning how to calculate a logarithm.
Mastering Logarithmic Calculations: Tips and Tricks
To become proficient in how to calculate a logarithm, it’s essential to develop effective problem-solving strategies and mental math techniques. One expert tip is to memorize key logarithmic identities and rules, such as the product rule and quotient rule, to simplify complex calculations. Additionally, practicing logarithmic calculations with different bases and values can help build confidence and fluency. Another approach is to use mental math tricks, such as estimating logarithmic values using nearby perfect powers, to quickly approximate calculations. Furthermore, developing a step-by-step approach to logarithmic problems can help individuals break down complex calculations into manageable parts. It’s also crucial to recognize when to use logarithmic tables or calculators to simplify calculations and avoid unnecessary complexity. By incorporating these tips and tricks into their problem-solving repertoire, individuals can master logarithmic calculations and unlock the full potential of logarithms in various fields. With consistent practice and application, individuals can develop a deep understanding of how to calculate a logarithm and tackle even the most challenging problems with ease.