Unveiling Portfolio Risk: A Practical Guide
Understanding portfolio risk is paramount for investors seeking to navigate the complexities of the financial markets. It allows for informed investment decisions and effective risk management. Portfolio risk represents the uncertainty associated with the returns of an investor’s collection of assets. A key aspect of evaluating this risk lies in understanding portfolio volatility. This volatility reflects the extent to which the value of a portfolio may fluctuate over time.
Several factors contribute to portfolio volatility, including the types of assets held and their interactions. Higher volatility signifies a potentially greater range of returns, both positive and negative. Investors need to assess their risk tolerance carefully. This assessment guides the construction of portfolios aligned with their financial goals and comfort levels. A crucial element in gauging this volatility involves understanding the concepts underlying the “standard deviation of the portfolio formula.” Although not explicitly stated here, these concepts are foundational to quantifying overall portfolio risk. Understanding the risks that impact the portfolio are extremely important to protect profit and also allow to make changes if needed.
Effective portfolio management begins with a clear understanding of portfolio risk. By carefully analyzing the factors that influence volatility, investors can construct portfolios designed to meet their individual needs and objectives. Ignoring the tools for calculating the “standard deviation of the portfolio formula”, or at least the fundamental ideas behind it, is not an option for the informed investor. Comprehending volatility provides a basis for more informed decision-making and ultimately, a greater chance of achieving long-term financial success and peace of mind. Properly using these risk measurements are the key to protect the capital, and increase the overall profit with the minimum risk possible.
How to Calculate Combined Investment Risk: A Step-by-Step Approach
Calculating portfolio risk involves understanding how the individual assets within the portfolio interact. The process moves beyond simply averaging the risk of each asset. It takes into account how the assets’ prices move in relation to each other. This relationship is crucial for determining the overall portfolio risk. While we won’t directly use the term “standard deviation of the portfolio formula” here, we’ll explore the concepts that underpin it.
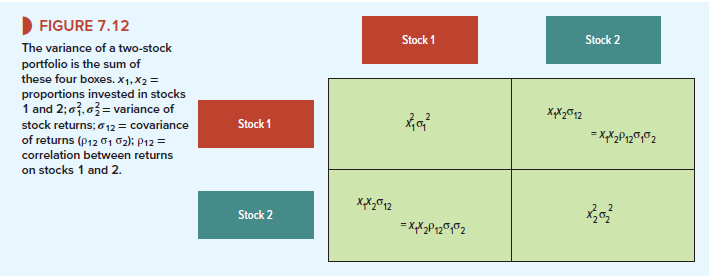
The first step involves assessing the variance of each individual asset in the portfolio. Variance measures how much an asset’s returns deviate from its average return. A higher variance indicates greater volatility. Next, consider the covariance between each pair of assets in the portfolio. Covariance measures how two assets move together. A positive covariance means that the assets tend to move in the same direction. A negative covariance means they tend to move in opposite directions. A covariance of zero means that the movements of the two assets are unrelated. Correlation is a standardized version of covariance. It ranges from -1 to +1. A correlation of +1 indicates perfect positive correlation. A correlation of -1 indicates perfect negative correlation. A correlation of 0 indicates no correlation. Understanding covariance and correlation is critical. It allows investors to quantify the diversification benefits within a portfolio. The “standard deviation of the portfolio formula” relies heavily on these relationships.
To calculate the overall portfolio risk, one must combine the individual asset variances. This involves weighting each variance by the square of the asset’s weight in the portfolio. Then, the covariances between all pairs of assets must be considered. These are also weighted by the product of the assets’ weights. The sum of these weighted variances and covariances gives the portfolio variance. The square root of the portfolio variance is the portfolio’s “standard deviation of the portfolio formula,” or volatility. This value represents the overall risk of the portfolio. Diversification benefits arise when assets have low or negative correlations. This reduces the overall portfolio volatility. This step-by-step approach provides a practical understanding of portfolio risk calculation. It emphasizes the importance of asset interaction. The insights provided are crucial for effective portfolio management.
Deconstructing the Components: Variance, Covariance, and Correlation
Understanding portfolio risk requires dissecting its fundamental components: variance, covariance, and correlation. These elements, while seemingly complex, provide crucial insights into how individual assets and their relationships contribute to overall portfolio volatility. Although we are not directly using the “standard deviation of the portfolio formula” here, its underlying principles are being explored.
Variance quantifies the risk associated with a single asset. It measures the dispersion of an asset’s returns around its average return. A higher variance indicates greater volatility and, consequently, higher risk. For example, a stock with a history of significant price swings will exhibit a higher variance than a stable bond. However, variance only tells part of the story. The “standard deviation of the portfolio formula” relies heavily on understanding how assets interact.
Covariance measures how two assets move in relation to each other. A positive covariance suggests that the assets tend to move in the same direction, while a negative covariance indicates they move in opposite directions. A covariance of zero implies no linear relationship. While covariance provides direction, it’s not standardized, making it difficult to compare across different asset pairs. This is where correlation becomes valuable. Correlation is a standardized measure of covariance, ranging from -1 to +1. A correlation of +1 signifies perfect positive correlation (assets move in lockstep), -1 indicates perfect negative correlation (assets move in opposite directions), and 0 suggests no linear correlation. For example, gold sometimes exhibits a negative correlation with stocks. This is a key factor in the standard deviation of the portfolio formula, as assets with low or negative correlation can significantly reduce overall portfolio risk. Consider a portfolio with stocks and bonds. If stocks decline, and bonds remain stable or increase in value due to their negative correlation, this offsets losses, reducing overall portfolio risk. Therefore, the interplay between variance, covariance, and correlation is central to understanding and managing portfolio risk, especially within the context of the concepts underlying the “standard deviation of the portfolio formula,” even without explicitly calculating it here.
Illustrative Examples: Calculating Portfolio Risk in Practice
Portfolio risk calculation is best understood through examples. Consider a hypothetical portfolio consisting of two assets: Stocks and Bonds. Let’s assume that 60% of the portfolio is allocated to stocks and 40% to bonds. Stocks have an expected return of 10% and a volatility (standard deviation) of 15%. Bonds have an expected return of 3% and a volatility of 5%. To calculate the overall portfolio risk, we also need to know how these two assets move in relation to each other, which is measured by their correlation.
Assume the correlation between stocks and bonds is 0.2. This indicates a low positive correlation, meaning they tend to move in the same direction, but not strongly. The “standard deviation of the portfolio formula” requires calculating the weighted variance of each asset and then adding twice the weighted covariance. The portfolio variance is calculated as: (0.6^2 * 0.15^2) + (0.4^2 * 0.05^2) + (2 * 0.6 * 0.4 * 0.2 * 0.15 * 0.05), resulting in 0.0094. Then we can find the square root of that result to derive the portfolio standard deviation. The square root of the portfolio variance is approximately 9.7%. This represents the portfolio’s overall risk level.
Now, consider another scenario. Suppose the correlation between the stocks and bonds were -0.2, indicating a slight inverse relationship. Using the same asset allocation and individual asset volatilities, the “standard deviation of the portfolio formula” changes, the covariance term would become negative. The portfolio variance calculation becomes (0.6^2 * 0.15^2) + (0.4^2 * 0.05^2) + (2 * 0.6 * 0.4 * -0.2 * 0.15 * 0.05), resulting in 0.0074. The square root of 0.0074 is approximately 8.6%. This lower portfolio volatility demonstrates the risk-reducing impact of including negatively correlated assets in a portfolio. This practical example showcases how the standard deviation of the portfolio formula translates to tangible results in portfolio management, highlighting the importance of asset allocation and correlation in managing investment risk. Note that the “standard deviation of the portfolio formula” provides an ex-ante risk measurement of the portfolio, or forecast of risk. Actual realized risk may differ substantially.
Optimizing Your Investment Mix: The Role of Diversification
Diversification is a crucial strategy for managing portfolio risk. It involves allocating investments across various asset classes. The goal is to reduce the impact of any single investment’s performance on the overall portfolio. Combining assets that don’t move in perfect lockstep can significantly lower portfolio volatility. This is because losses in one asset can be offset by gains in another, leading to more stable returns. The effectiveness of diversification hinges on the correlation between assets. Assets with low or negative correlations offer the greatest risk reduction benefits.
The standard deviation of the portfolio formula helps to quantify the benefits of diversification. By understanding the relationships between assets, investors can construct portfolios that are less susceptible to market fluctuations. However, diversification is not a foolproof strategy. It doesn’t guarantee profits or prevent losses in a market downturn. In fact, during periods of extreme market stress, correlations between assets tend to increase, diminishing the benefits of diversification. While the standard deviation of the portfolio formula provides a valuable framework, it’s crucial to remember that diversification is a tool for managing risk, not eliminating it.
Different diversification strategies exist, each with its own benefits and drawbacks. A simple strategy might involve allocating investments across stocks, bonds, and real estate. More sophisticated strategies might incorporate international equities, commodities, or alternative investments like hedge funds. The optimal diversification strategy depends on an investor’s risk tolerance, investment goals, and time horizon. Over-diversification can also be a concern. Adding too many assets to a portfolio can dilute returns and increase transaction costs. Therefore, investors should carefully consider the number and type of assets included in their portfolios. The standard deviation of the portfolio formula serves as a guide to understanding how different assets, especially those with low or negative correlation, influence overall portfolio risk. Understanding the standard deviation of the portfolio formula allows investors to see how diversification impacts their overall portfolio risk. It’s important to note that factors beyond the standard deviation of the portfolio formula, such as management fees and taxes, should also be considered when making investment decisions. A well-diversified portfolio, constructed with an understanding of the standard deviation of the portfolio formula, can provide a more stable and predictable investment experience.
Factors Influencing Portfolio Risk: Beyond the Formula
While quantitative measures like the “standard deviation of the portfolio formula” provide a valuable framework for assessing portfolio risk, it is crucial to understand that numerous qualitative factors can also significantly impact investment outcomes. The inherent risk characteristics of each asset class within the portfolio are primary considerations. For example, equities are generally considered riskier than government bonds due to their greater price volatility. However, even within asset classes, there may be significant differences. Emerging market equities are generally riskier than developed market equities.
The macroeconomic environment plays a pivotal role in shaping portfolio risk. Factors like inflation, interest rates, economic growth, and geopolitical events can all influence asset prices and portfolio volatility. Changes in these factors can lead to unexpected market movements and impact the accuracy of risk assessments based solely on historical data. Investment horizon is another critical factor. A longer investment horizon allows investors to ride out short-term market fluctuations and potentially benefit from long-term growth trends. Conversely, a shorter investment horizon may require a more conservative portfolio allocation to minimize the risk of capital losses.
Furthermore, it’s important to acknowledge the limitations of relying solely on the “standard deviation of the portfolio formula” as a comprehensive risk measure. Volatility, as captured by the “standard deviation of the portfolio formula,” is only one aspect of risk. It doesn’t capture other potential risks like liquidity risk, credit risk, or regulatory risk. Therefore, it is crucial to supplement volatility analysis with other risk management techniques such as stress-testing and scenario planning. Stress-testing involves simulating the impact of extreme market events on the portfolio, while scenario planning involves developing and analyzing different plausible economic scenarios and their potential impact on investment outcomes. These techniques can help investors better understand and prepare for a wider range of potential risks beyond those captured by the “standard deviation of the portfolio formula”. Understanding and managing these factors effectively is crucial for making informed investment decisions and achieving long-term financial goals. While the “standard deviation of the portfolio formula” provides a starting point, a holistic approach to risk assessment is essential. The “standard deviation of the portfolio formula” serves as just one tool in risk assessment.
Tools and Resources for Portfolio Risk Assessment
Assessing portfolio risk can be streamlined using a variety of readily available tools and resources. While understanding the underlying principles of risk calculation, like those related to the “standard deviation of the portfolio formula”, is crucial, these tools can significantly simplify the process for investors. Several online portfolio trackers offer risk assessment features, allowing investors to gain insights into their portfolio’s potential volatility. These platforms often utilize algorithms to estimate risk metrics, aiding in informed decision-making. However, it is important to remember that these tools are only as good as the data and assumptions they rely on, and an understanding of concepts related to the “standard deviation of the portfolio formula” can improve the investor’s results.
Risk management software provides more sophisticated analysis, enabling users to stress-test their portfolios under various scenarios. Such software often incorporates factors beyond simple volatility calculations, like macroeconomic conditions or interest rate changes, to provide a more comprehensive risk profile. Financial advisor services also represent a valuable resource, especially for investors who prefer personalized guidance. Financial advisors can assess an investor’s risk tolerance, investment goals, and time horizon to construct a suitable portfolio and monitor its risk levels over time. When evaluating the output of any of these tools, comparing the results with the “standard deviation of the portfolio formula”, or its underlying concepts will help improve the validity of the results.
Examples of tools available to investors include online portfolio trackers like Morningstar Portfolio Manager and Personal Capital. These tools enable investors to monitor their asset allocation, track performance, and assess risk metrics. While these tools can be helpful in assessing risk, a deeper understanding of the “standard deviation of the portfolio formula” enables investors to critically evaluate the tool’s outputs and make more informed investment decisions. In fact, some features can even allow investors to input data to calculate the “standard deviation of the portfolio formula”. The key is to complement the use of any tools with a solid understanding of risk management principles. Therefore, while these tools and resources can be valuable aids, investors should always exercise due diligence and seek professional advice when needed, particularly when dealing with complex investment strategies or substantial portfolios.
Advanced Concepts: Expanding Your Understanding of Portfolio Risk
Beyond basic volatility, a deeper dive into portfolio risk assessment reveals sophisticated measures. While understanding the basics of how assets combine to impact portfolio risk is essential, methodologies like Value at Risk (VaR) and Expected Shortfall offer more nuanced perspectives. These advanced concepts provide alternative lenses through which investors can evaluate potential losses.
Value at Risk (VaR) estimates the maximum loss expected over a specific time horizon with a certain confidence level. For example, a one-day VaR of $1 million at a 95% confidence level suggests there is a 5% chance of losing more than $1 million in a single day. Expected Shortfall, also known as Conditional Value at Risk (CVaR), goes a step further. It calculates the expected loss, given that the loss exceeds the VaR threshold. In essence, it quantifies the average loss that could be incurred in the worst-case scenarios, providing a more complete picture of tail risk. These risk metrics are extensions of the principles used in the “standard deviation of the portfolio formula>”, giving a probable range of potential outcomes. However, instead of simply looking at the distribution of all returns, these measures focus on the left tail of the distribution – the losses. Keep in mind that these concepts are built upon an understanding of how portfolio volatility is derived. The standard deviation of the portfolio formula serves as a foundational element for estimating potential losses.
Although VaR and Expected Shortfall offer valuable insights, they also have limitations. These models rely on assumptions about the distribution of asset returns, which may not always hold true in reality. Furthermore, they may not fully capture the impact of extreme events or “black swan” events. Understanding these limitations is crucial for interpreting the results and making informed decisions. While the standard deviation of the portfolio formula provides a single number summarizing risk, VaR and Expected Shortfall offer a more scenario-based risk analysis, focusing on the magnitude of potential losses. It is important to remember the standard deviation of the portfolio formula, while useful, provides a more basic understanding of risk. These advanced measures build on those concepts to offer a more sophisticated and insightful evaluation of potential investment risks. These measures don’t negate the usefulness of the standard deviation of the portfolio formula, but enrich the understanding of risk management.