What is a Zero-Coupon Bond?
A zero-coupon bond is a debt security that doesn’t pay periodic interest payments. Instead, it’s bought at a discount to its face value. At maturity, the investor receives the bond’s face value. This difference between the purchase price and the face value represents the investor’s return. For example, imagine a zero-coupon bond with a face value of $1,000 and a maturity date in five years. An investor might purchase this bond today for $800. At maturity, they receive $1,000, earning a profit of $200. Understanding the macaulay duration of zero coupon bond is crucial for assessing its risk and return profile. The macaulay duration of zero coupon bond is a key metric for investors.
Zero-coupon bonds offer a simple investment strategy. Their return is solely determined by the difference between the purchase price and the face value. The longer the time to maturity, the greater the potential return, but also the higher the interest rate risk. The macaulay duration of zero coupon bond helps investors quantify this risk. It’s essential to note that the price of a zero-coupon bond fluctuates inversely with interest rate changes. Rising interest rates decrease the bond’s present value, while falling rates increase it. Therefore, the macaulay duration of zero coupon bond is a critical factor in investment decisions.
Investors need to consider several factors before investing in zero-coupon bonds. These include the creditworthiness of the issuer, the time until maturity, and the prevailing interest rate environment. A longer time to maturity exposes the investor to greater interest rate risk. Calculating the macaulay duration of zero coupon bond allows investors to understand this risk quantitatively. This allows for more informed decision-making, aligning investment choices with the investor’s risk tolerance and financial objectives. The macaulay duration of zero coupon bond provides a valuable measure of this interest rate sensitivity.
Time Value and the Price of a Zero-Coupon Bond
The price of a zero-coupon bond is fundamentally linked to its face value, the time until it matures, and the prevailing interest rates in the market. Investors purchase these bonds at a discount to their face value. This discount reflects the time value of money; a dollar received today is worth more than a dollar received in the future due to its potential earning capacity. To determine the current price, one must discount the future face value back to its present value. This process uses the prevailing market interest rate (or yield to maturity) as the discount rate. A higher interest rate results in a lower present value, meaning a lower price for the bond. Conversely, a lower interest rate leads to a higher present value and a higher price. Understanding this relationship is key to comprehending the price fluctuations of zero-coupon bonds and the implications for the macaulay duration of zero coupon bond.
The discounting process involves calculating the present value of the future cash flow (the face value at maturity). The formula for present value is: PV = FV / (1 + r)^n, where PV is the present value, FV is the face value, r is the interest rate (yield to maturity), and n is the number of years to maturity. For example, a $1,000 zero-coupon bond maturing in 5 years with a prevailing interest rate of 5% would have a present value of approximately $783.53. This calculation is crucial for determining the current market price of a zero-coupon bond, and in turn, understanding its macaulay duration of zero coupon bond. Changes in interest rates directly impact this present value and thus the bond’s price, highlighting the importance of considering interest rate risk.
Investors use the present value calculation extensively to compare different investment opportunities. They consider the time to maturity and interest rates to ensure the bond offers a sufficient return relative to its risk. The present value also forms the basis for calculating other important bond metrics, including the macaulay duration of zero coupon bond. This metric helps investors understand the bond’s sensitivity to interest rate changes. A longer time to maturity means a larger discount, and consequently, a greater price sensitivity to interest rate fluctuations. This concept is fundamental to informed investment decisions, especially when considering the macaulay duration of zero coupon bond.
Introducing Macaulay Duration
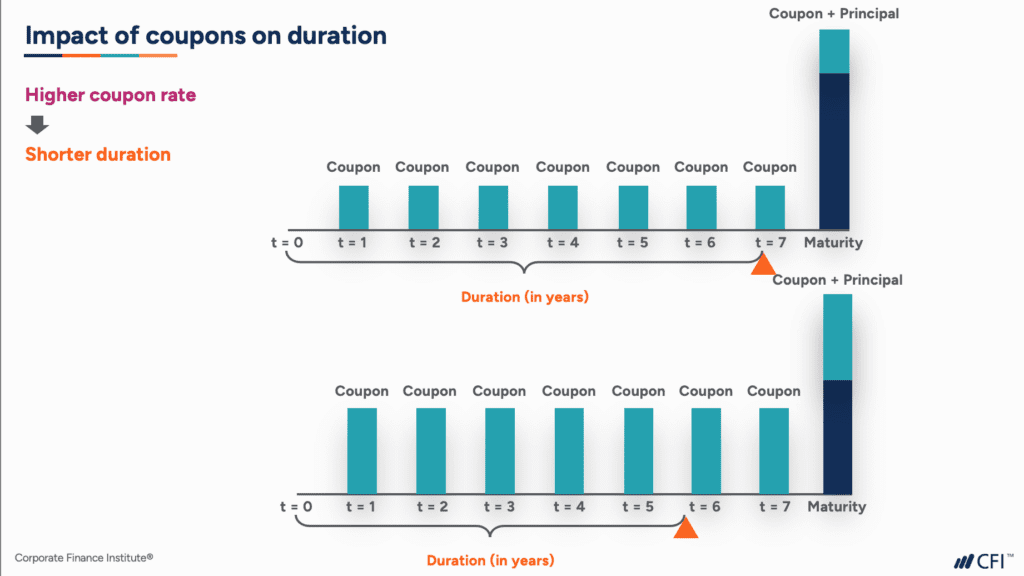
Macaulay duration measures a bond’s sensitivity to interest rate changes. It represents the weighted average time until each cash flow is received. The weights are the present values of those cash flows. This means it considers both the timing and the value of future payments. For a standard bond, this involves multiple cash flows (coupon payments and principal repayment). However, the Macaulay duration of zero coupon bond simplifies considerably. Since zero-coupon bonds only have one cash flow—the face value at maturity—calculating its Macaulay duration is particularly straightforward.
The Macaulay duration of a zero-coupon bond is directly related to its time to maturity. A longer time to maturity results in a longer Macaulay duration. This is because the single cash flow is further into the future. The calculation effectively tells investors the average time they’ll wait to receive their investment back. Understanding the Macaulay duration of zero coupon bond is crucial for assessing interest rate risk. A higher Macaulay duration indicates greater sensitivity to interest rate fluctuations. A small change in interest rates will have a more significant impact on the bond’s price if its Macaulay duration is longer. Investors use this measure to make informed decisions about bond selection and portfolio construction. The Macaulay duration of zero coupon bond allows investors to gauge the duration of their investments before making any decisions.
For zero-coupon bonds, the Macaulay duration is simply the time to maturity. This makes it an exceptionally useful metric for these types of bonds. Unlike other bonds with multiple cash flows, the Macaulay duration of zero coupon bond doesn’t require complex calculations involving present values of various payments. It provides a clear and concise measure of the bond’s interest rate risk. This makes it valuable for investors seeking to understand the investment’s sensitivity to changes in market conditions. Therefore, accurately calculating the Macaulay duration of zero coupon bond is critical for risk management.
Calculating Macaulay Duration for a Zero-Coupon Bond: A Simple Formula
The Macaulay duration of a zero-coupon bond is straightforward to calculate because it involves only one cash flow—the face value at maturity. The formula for the Macaulay duration of a zero-coupon bond is simply the time to maturity. This is because the present value weighting in the general Macaulay duration formula simplifies to 1 when dealing with a single future payment. Therefore, the weighted average time until cash flow receipt directly equals the time to maturity. This makes the Macaulay duration of a zero-coupon bond a particularly useful metric. Understanding the Macaulay duration of zero coupon bond is crucial for effective portfolio management.
Let’s illustrate this with an example. Consider a zero-coupon bond with a face value of $1,000 and a maturity of five years. To calculate the Macaulay duration, one simply uses the maturity as the direct measure. In this case, the Macaulay duration is 5 years. This means that the weighted average time until the investor receives their investment back is five years. This simple calculation highlights the ease of determining the Macaulay duration of zero coupon bond compared to coupon-bearing bonds. The simplicity stems from the absence of periodic interest payments, which simplifies the present value weighting calculation.
The formula can be expressed as: Macaulay Duration = Time to Maturity. This direct relationship between Macaulay duration and time to maturity for zero-coupon bonds provides a quick and easy way to assess the interest rate sensitivity of these instruments. Investors frequently utilize this characteristic of the Macaulay duration of zero coupon bond when evaluating their portfolio’s exposure to interest rate risk. A longer time to maturity indicates a higher Macaulay duration and thus greater sensitivity to interest rate fluctuations. Conversely, a shorter maturity results in a lower Macaulay duration and reduced interest rate risk. Therefore, understanding the Macaulay duration of zero coupon bond is an essential aspect of effective investment decision-making.
How to Interpret Macaulay Duration in Investment Decisions
Understanding the Macaulay duration of a zero-coupon bond is crucial for managing interest rate risk. A higher Macaulay duration indicates greater sensitivity to interest rate fluctuations. If interest rates rise, the price of a bond with a longer Macaulay duration will fall more sharply than that of a bond with a shorter duration. Conversely, if interest rates decline, the price of a longer-duration bond will increase more significantly. Investors can use this understanding to manage their portfolios effectively.
For instance, a conservative investor with a low risk tolerance might prefer zero-coupon bonds with shorter Macaulay durations. This strategy limits potential losses from rising interest rates. In contrast, an investor seeking higher returns and willing to accept greater risk might favor zero-coupon bonds with longer Macaulay durations, potentially benefiting from larger price increases when interest rates fall. The Macaulay duration of zero-coupon bond is a key factor in this investment decision-making process. It allows investors to tailor their bond holdings to align with their specific risk profiles and return objectives.
Effective portfolio construction involves considering the Macaulay durations of all bond holdings. Diversification across bonds with varying durations can help mitigate overall interest rate risk. By strategically managing the average Macaulay duration of a portfolio, investors can fine-tune their exposure to interest rate changes. Therefore, mastering the concept of Macaulay duration of a zero-coupon bond empowers investors to make informed choices, optimizing their portfolios for their desired risk-return balance. This knowledge contributes to a more robust and resilient investment strategy.
Macaulay Duration vs. Modified Duration: Key Differences
While Macaulay duration provides a valuable measure of a bond’s interest rate sensitivity, especially the Macaulay duration of zero coupon bond, modified duration offers a slightly different perspective. Modified duration refines Macaulay duration to better approximate the percentage change in a bond’s price in response to a small change in interest rates. This is particularly useful for portfolio management and risk assessment.
The calculation of modified duration involves dividing the Macaulay duration by (1 + yield to maturity). For zero-coupon bonds, this calculation is straightforward due to the single cash flow at maturity. The Macaulay duration of zero coupon bond is simply the time to maturity. Therefore, the modified duration for a zero-coupon bond is also easily calculated. Understanding both Macaulay and modified duration enhances a comprehensive understanding of interest rate risk associated with zero-coupon bonds. The difference between these durations highlights their respective roles in assessing interest rate sensitivity.
It’s important to note that this distinction isn’t the primary focus of this article on the Macaulay duration of zero coupon bond. However, understanding the relationship between Macaulay and modified duration provides a more complete picture of interest rate risk management. While Macaulay duration provides a weighted average time to cash flows, modified duration offers a more direct measure of price sensitivity to interest rate changes. This distinction is crucial for sophisticated portfolio strategies and risk mitigation. The Macaulay duration of zero coupon bond, a simpler case, serves as a useful foundation for grasping this distinction before moving to more complex bond structures.
Practical Applications of Macaulay Duration in Portfolio Management
Understanding the Macaulay duration of zero-coupon bonds is crucial for effective portfolio management. Investors can use this metric to construct an immunized portfolio, designed to protect against interest rate fluctuations. By carefully selecting zero-coupon bonds with durations that match the investor’s liability horizon, a portfolio can be created where the value of the assets and liabilities move in tandem, mitigating interest rate risk. The Macaulay duration of zero-coupon bond helps investors to appropriately match assets and liabilities and minimize risk.
Another key application involves hedging interest rate risk. If an investor anticipates rising interest rates, they might shorten the Macaulay duration of their bond portfolio by investing in shorter-term zero-coupon bonds. This reduces the portfolio’s sensitivity to interest rate increases. Conversely, if rates are expected to fall, lengthening the Macaulay duration through longer-term zero-coupon bonds can potentially enhance returns. Effective use of the Macaulay duration of zero coupon bond allows for strategic adjustments to portfolio composition based on interest rate forecasts.
Consider a pension fund managing long-term liabilities. The fund manager can use zero-coupon bonds with carefully selected durations to match the timing of future pension payouts. This helps ensure that sufficient funds will be available to meet those obligations regardless of interest rate movements. Similarly, an insurance company dealing with long-term policy payouts can benefit from employing the Macaulay duration of zero-coupon bonds to match asset durations with liability durations. Such strategies rely heavily on precise duration management to minimize risks associated with interest rate volatility. The Macaulay duration of zero-coupon bonds provides a powerful tool for managing the interest rate risk inherent in these types of long-term liabilities. Careful consideration of Macaulay duration allows for more effective asset-liability management.
Limitations of Macaulay Duration and Considerations for Advanced Analysis
While Macaulay duration provides a valuable measure of interest rate sensitivity for zero-coupon bonds, it’s crucial to acknowledge its limitations. A core assumption underlying Macaulay duration is a constant interest rate environment. In reality, interest rates fluctuate. This fluctuation can impact the accuracy of the Macaulay duration of zero-coupon bond’s prediction of price changes, especially over longer time horizons. The formula doesn’t account for the reinvestment risk associated with coupon payments, which is irrelevant for zero-coupon bonds but important for other bond types. Therefore, the Macaulay duration of zero coupon bond calculation might underestimate or overestimate the true interest rate sensitivity in dynamic market conditions.
Furthermore, Macaulay duration is best suited for simple bonds. Its application becomes less precise when dealing with more complex instruments. Bonds with embedded options, such as callable bonds or putable bonds, present scenarios where Macaulay duration may not accurately reflect interest rate sensitivity. These options alter the bond’s cash flow profile, making the simple weighted average time calculation less reliable. For these instruments, more sophisticated metrics like effective duration are necessary to capture the impact of interest rate changes more accurately. Effective duration accounts for how the optionality influences the bond’s price changes. The Macaulay duration of zero-coupon bond, however, remains a powerful and straightforward tool for understanding the interest rate risk of these simpler instruments.
For investors focused on zero-coupon bonds, understanding the Macaulay duration of zero coupon bond is a valuable skill. It provides a clear and readily calculable measure of interest rate risk. However, remember that its application should be confined to its strengths: the analysis of simple, non-callable, and non-putable zero-coupon bonds. For more complex fixed-income securities, investors should explore and utilize more advanced duration measures to ensure a comprehensive assessment of interest rate risk. Ignoring the limitations of Macaulay duration can lead to inaccurate estimations and potentially poor investment decisions. Always consider the specific characteristics of the bond and the market environment before relying solely on Macaulay duration for investment analysis. The accurate calculation of the Macaulay duration of zero coupon bond is essential, but a balanced approach incorporating market context is vital.