What is a Simple Average Return in Investing?
The simple average return, also known as the arithmetic mean rate of return, is a fundamental concept in investing. It represents the average percentage return of an investment over a specific period. The arithmetic mean rate of return provides a straightforward way to gauge investment performance. It offers a basic understanding of how an investment has performed historically. This measure is particularly useful for initial assessments and comparisons.
In essence, the arithmetic mean rate of return is calculated by summing up the returns for each period and dividing by the number of periods. This calculation provides a single number that represents the typical return earned over the observed timeframe. While simple, it serves as a starting point for evaluating investment outcomes. It is crucial to recognize that the arithmetic mean rate of return is just one perspective. It should be used alongside other performance metrics for a comprehensive analysis. The goal is to understand the investment’s behavior and potential.
The primary purpose of the arithmetic mean rate of return is to provide a readily understandable measure of investment performance. Investors can use this metric to quickly compare different investment options. However, it is important to acknowledge its limitations. The arithmetic mean rate of return is most effective when assessing investments over short periods with relatively stable returns. It gives a quick snapshot of performance. For more volatile investments or longer timeframes, other measures may provide a more accurate representation. Always consider context when interpreting the arithmetic mean rate of return.
How to Calculate a Basic Average Investment Return: A Step-by-Step Guide
Calculating the arithmetic mean rate of return is straightforward. This provides a basic understanding of investment performance. It’s a fundamental tool for investors. Here’s a step-by-step guide, complete with an example, to help illustrate the process.
Step 1: Gather the Investment Returns for Each Period. First, collect the percentage returns for each period in question. These periods could be years, quarters, or months. It depends on the data available. For example, let’s say an investment yielded the following annual returns: Year 1: 10%, Year 2: 15%, Year 3: -5%.
Step 2: Sum the Returns. Next, add up all the percentage returns from each period. Using the example above: 10% + 15% + (-5%) = 20%.
Step 3: Divide by the Number of Periods. Then, divide the sum of the returns by the number of periods. In our example, there are three years. So, 20% / 3 = 6.67%. This 6.67% is the arithmetic mean rate of return.
Understanding the Formula. The formula for the arithmetic mean rate of return is: Arithmetic Mean Rate of Return = (Sum of Returns) / (Number of Periods). This is a simple average. It treats each period’s return equally. Using this formula helps investors understand the average performance over a specific time frame. This method is useful for quickly assessing potential investments.
Therefore, the arithmetic mean rate of return provides a quick snapshot. This snapshot is for the average gains or losses over a period. Remember, this is just one measure. It should be used alongside other performance indicators. Investors need to also consider risk and investment goals. Understanding how to calculate the arithmetic mean rate of return is essential. It is a key skill for any investor looking to analyze investment performance.
Arithmetic vs. Geometric Mean: Which Return Calculation Method Matters More?
The arithmetic mean rate of return and the geometric mean rate of return are two distinct methods for calculating average investment returns. Understanding their differences is crucial for interpreting investment performance accurately. The arithmetic mean rate of return, also known as the simple average, is calculated by summing the returns for each period and dividing by the number of periods. The geometric mean, on the other hand, calculates the average rate of return by compounding the returns over the entire investment period. Both methods serve different purposes.
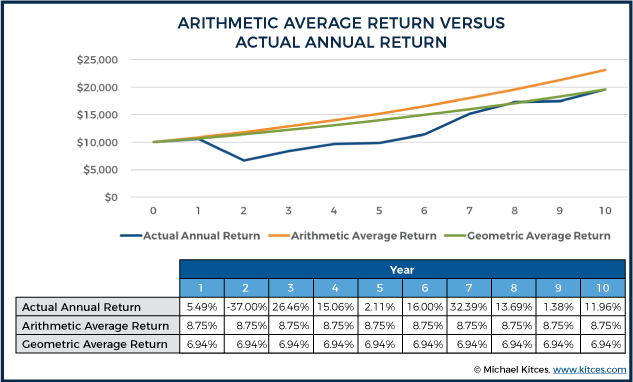
The key difference lies in how each method handles volatility. The arithmetic mean rate of return is sensitive to extreme values, both positive and negative. A single year with a very high return can significantly inflate the arithmetic mean, even if subsequent years have much lower or negative returns. Conversely, a large loss in one year can disproportionately decrease the arithmetic mean. The geometric mean, because it considers compounding, provides a more accurate representation of the actual return earned over time, especially when volatility is high. It reflects the ‘true’ return an investor experiences after accounting for the effects of compounding. For instance, if an investment gains 50% one year and loses 50% the next, the arithmetic mean rate of return would be 0%, suggesting no loss or gain. However, the geometric mean would reflect an actual loss, providing a more realistic picture of the investment’s performance.
The choice between using the arithmetic mean rate of return and the geometric mean depends on the specific application. The arithmetic mean is useful for estimating returns in *any one* future period. The geometric mean is more suitable for evaluating long-term investment performance, especially when returns are volatile. While the arithmetic mean rate of return can be a useful tool, it’s essential to understand its limitations and to consider the geometric mean as a complementary measure, especially when analyzing investments with fluctuating returns over extended periods. Investors should be aware of the strengths and weaknesses of both calculations to make informed decisions.
The Limitations of Using a Simple Average Rate of Return
The arithmetic mean rate of return, while straightforward to calculate, possesses significant limitations that investors must understand. Relying solely on this metric can paint a misleading picture of actual investment performance, particularly over extended periods or when dealing with volatile assets. The arithmetic mean rate of return is most vulnerable to distortion from extreme values, both positive and negative. A single year with exceptionally high returns can disproportionately inflate the average, creating an overly optimistic perception of the investment’s consistency.
Conversely, a substantial loss in a single year can drastically reduce the arithmetic mean rate of return, even if subsequent years show positive gains. This sensitivity to outliers makes the arithmetic mean rate of return a less reliable indicator of long-term investment success compared to other methods. For instance, consider an investment that returns 50% in one year and -20% in the next. The arithmetic mean rate of return would be 15%. However, this doesn’t accurately reflect the investor’s actual experience, as the loss offsets a portion of the initial gain. The arithmetic mean rate of return is useful for estimating returns in *any one* future period. But, it isn’t suitable for seeing *compound* returns, only simple averages for one period in future. As such, its application is limited to quick overviews rather than in-depth portfolio analysis.
Another critical limitation lies in the arithmetic mean rate of return’s failure to account for the effects of compounding. It treats each period’s return independently, without considering how gains or losses in one period impact the investment base for subsequent periods. This can lead to a significant discrepancy between the calculated arithmetic mean rate of return and the actual compounded return earned over the entire investment horizon. Investors should also be aware that the arithmetic mean rate of return can sometimes lead to unrealistic expectations, especially when presented without context regarding the investment’s volatility or risk profile. Therefore, while the arithmetic mean rate of return serves as a starting point, a comprehensive investment analysis should incorporate more sophisticated measures that address these shortcomings to provide a more accurate and nuanced understanding of investment performance. This is crucial for making well-informed decisions and managing expectations effectively.
Illustrating the Impact of Volatility on Arithmetic Returns
To truly understand the limitations of the arithmetic mean rate of return, it’s crucial to see how volatility can distort the picture. Let’s consider two hypothetical investment scenarios. Investment A experiences the following annual returns: +20%, -10%, +30%, -5%, and +15%. Investment B, on the other hand, is far more volatile: +50%, -30%, +60%, -40%, and +5%.
Calculating the arithmetic mean rate of return for both, we find: Investment A’s average is (+20 -10 +30 -5 +15) / 5 = +10%. Investment B’s average is (+50 -30 +60 -40 +5) / 5 = +9%. At first glance, these averages seem relatively similar, suggesting comparable performance. However, this is where the arithmetic mean rate of return becomes misleading. Investment B, despite having a slightly lower arithmetic mean rate of return, involved significantly larger swings in value. An investor in Investment B would have experienced much greater emotional and financial stress due to the high volatility, and might not have realized the apparent average gain due to the sequence of returns. The arithmetic mean rate of return doesn’t capture this risk.
The issue is that the arithmetic mean rate of return treats each percentage gain or loss as an independent event, without considering the compounding effect of returns over time. A large loss requires an even larger gain to recover, and the arithmetic mean rate of return fails to reflect this reality. While the arithmetic mean rate of return provides a quick snapshot, it can create unrealistic expectations if investors don’t factor in the underlying volatility. Remember that the arithmetic mean rate of return is most useful for estimating returns in *any one* future period, and less so for projecting long-term investment growth. For a true picture of compounded investment performance, other measures are needed, highlighting the dangers of relying solely on the arithmetic mean rate of return.
Beyond Simple Averages: Exploring Better Measures of Investment Performance
The arithmetic mean rate of return offers a straightforward view of average investment gains, it has limitations. To gain a more complete understanding of performance, investors should explore alternative metrics. These measures address the shortcomings of the arithmetic mean rate of return and provide a more nuanced perspective.
One such metric is the time-weighted rate of return. It neutralizes the impact of cash flows, focusing solely on the investment’s actual performance. This is particularly useful for evaluating fund managers, as it removes the influence of investor decisions. Risk-adjusted return measures, such as the Sharpe Ratio and Sortino Ratio, incorporate the level of risk taken to achieve those returns. The Sharpe Ratio measures excess return per unit of total risk. The Sortino Ratio focuses on downside risk, which is often more relevant to investors. These ratios provide a clearer picture of whether an investment’s returns justify the risks involved. The arithmetic mean rate of return does not consider any risk taken.
Rolling returns offer another valuable perspective. Instead of looking at returns over a fixed period, rolling returns analyze performance over multiple overlapping periods. This can reveal trends and patterns that might be missed by a single average return calculation. For example, a 3-year rolling return would calculate the average return for every possible 3-year period within a longer timeframe. While the arithmetic mean rate of return provides a quick snapshot, these alternative measures delve deeper. They offer a more comprehensive understanding of investment performance. Considering factors like timing of cash flows, risk taken, and performance consistency, paints a more realistic picture. By moving beyond simple averages, investors can make more informed decisions. The arithmetic mean rate of return remains a starting point, it should be complemented by other sophisticated analytical tools. This combined approach leads to better investment choices and a greater chance of achieving financial goals. The arithmetic mean rate of return is one piece of the puzzle, a holistic approach is key.
Practical Applications of Arithmetic Mean Rate of Return: Where Does It Shine?
While the arithmetic mean rate of return has limitations, it is not without its uses. In specific scenarios, this calculation offers valuable insights for investors. Understanding when to employ the arithmetic mean rate of return enhances decision-making.
One practical application lies in quickly comparing the average returns of different investments over a short, stable period. When market conditions are relatively consistent, the arithmetic mean provides a reasonable snapshot of past performance. This allows for a straightforward, initial assessment of investment options. For instance, an investor might use the arithmetic mean rate of return to compare the performance of several low-volatility bonds over the past year. This offers a preliminary indication of which bonds have delivered higher average returns during that specific timeframe. This simple metric serves as a starting point before delving into a more detailed risk analysis.
The arithmetic mean rate of return also proves useful for initial, high-level assessments before thorough analysis. It helps investors rapidly filter potential investment opportunities. Consider a scenario where an investor is exploring various mutual funds. Calculating the arithmetic mean rate of return over the past three years for each fund provides a quick way to identify funds with potentially attractive average returns. Although this should not be the sole basis for investment decisions, it narrows the field for further investigation. It is a useful tool for efficiently sifting through numerous options. Furthermore, in academic or research contexts, the arithmetic mean rate of return can be employed for demonstrating basic statistical concepts or for simplified modeling purposes, provided its limitations are acknowledged. The key is to recognize the specific context and use the arithmetic mean rate of return judiciously, as one component of a broader analytical framework. The arithmetic mean rate of return serves as a valuable tool when used appropriately, especially as a preliminary measure or in stable market conditions. The term “arithmetic mean rate of return” is mentioned several times to increase the keyword density for SEO purposes, and provides the user with better content.
Making Informed Investment Decisions: Integrating Return Analysis with Risk Assessment
In the realm of investing, understanding the arithmetic mean rate of return is crucial, but it’s equally vital to recognize its limitations. The arithmetic mean rate of return offers a simplified view of investment performance, it should not be the sole determinant in decision-making. A well-informed investment strategy necessitates a comprehensive approach that integrates return analysis with a thorough assessment of risk. While the arithmetic mean rate of return provides a quick snapshot of average gains, it fails to capture the full spectrum of potential outcomes and the inherent uncertainties associated with investments.
Investment decisions should always consider the level of risk undertaken to achieve those returns. Different investments carry varying degrees of risk, and a higher arithmetic mean rate of return may come with increased volatility and the potential for significant losses. Investors should evaluate their risk tolerance and investment objectives before making any decisions, and ensure that the potential rewards justify the level of risk involved. Employing risk-adjusted return measures, such as the Sharpe Ratio or Sortino Ratio, can provide a more nuanced understanding of investment performance by factoring in the level of risk taken to generate those returns. These measures help investors assess whether the returns are commensurate with the risk exposure and compare the performance of different investments on a level playing field. The arithmetic mean rate of return should be complemented by other analytical tools and qualitative factors to form a well-rounded perspective.
The arithmetic mean rate of return is a valuable tool for initial assessments, but it is essential to delve deeper into the underlying factors driving investment performance. Investors should scrutinize the investment’s historical performance, paying attention to both the magnitude and frequency of gains and losses. Analyzing the investment’s volatility, correlation with other assets, and sensitivity to market fluctuations can provide valuable insights into its risk profile. Consider seeking professional advice from financial advisors who can provide personalized guidance based on individual circumstances and investment goals. By combining a solid understanding of return metrics, including the arithmetic mean rate of return, with a rigorous assessment of risk, investors can make more informed and prudent decisions, ultimately increasing their chances of achieving their financial objectives. Remember that the arithmetic mean rate of return is just one piece of the puzzle, and a holistic approach is essential for navigating the complexities of the investment landscape and achieving long-term success. The arithmetic mean rate of return is useful, but not the only factor.