Unlocking the Power of Random Processes in Finance
In the realm of finance, uncertainty and randomness are inherent components of the market landscape. To navigate these complexities, financial professionals rely on stochastic calculus, a branch of mathematics that deals with the analysis of random processes. Shreve stochastic calculus for finance, in particular, has emerged as a powerful tool for modeling and managing financial risk. By applying stochastic calculus to financial problems, practitioners can better understand and quantify the uncertainties that drive market fluctuations. This, in turn, enables them to make more informed investment decisions, optimize portfolio performance, and develop more accurate risk management strategies. In the context of finance, stochastic calculus has far-reaching applications, including option pricing, risk management, and portfolio optimization. As the financial landscape continues to evolve, the importance of Shreve stochastic calculus for finance will only continue to grow.
Understanding the Fundamentals of Stochastic Calculus
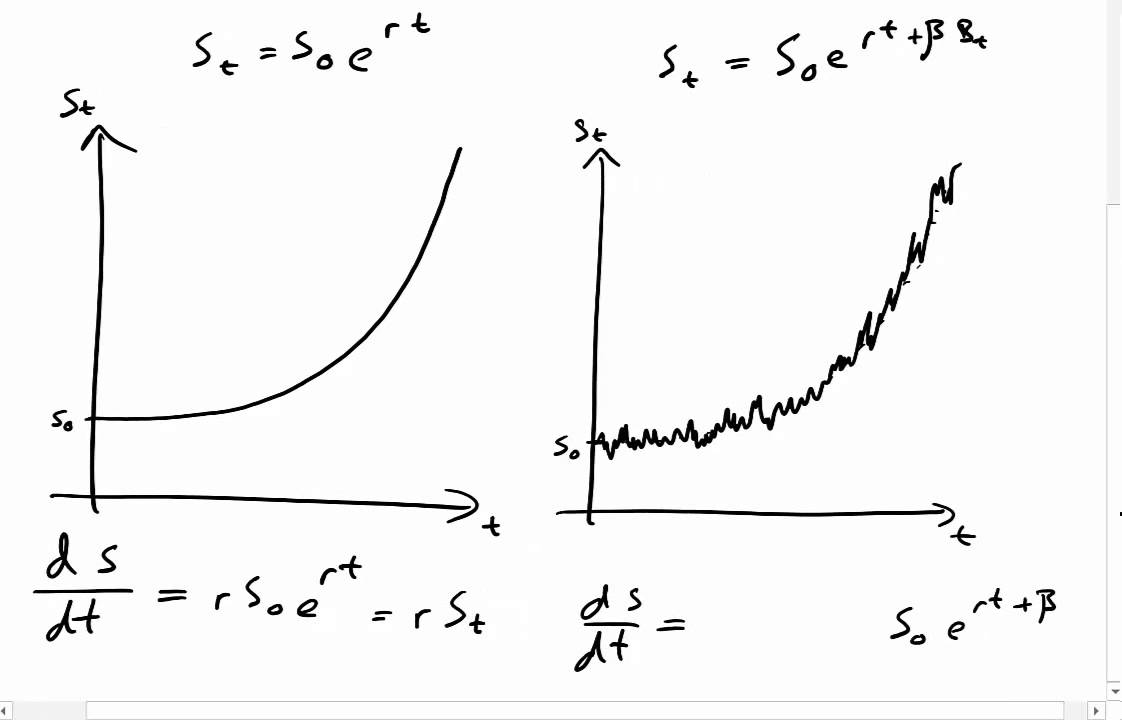
Stochastic calculus is a branch of mathematics that deals with the analysis of random processes. At its core, stochastic calculus is built around three fundamental concepts: Brownian motion, Ito’s lemma, and stochastic integrals. Brownian motion, named after Scottish botanist Robert Brown, is a mathematical model that describes the random movement of particles suspended in a fluid. In the context of finance, Brownian motion is used to model stock prices and other financial assets. Ito’s lemma, developed by Japanese mathematician Kiyoshi Ito, is a crucial tool for analyzing stochastic processes. It provides a framework for understanding how functions change over time, taking into account the randomness of the underlying process. Stochastic integrals, a concept closely related to Ito’s lemma, are used to calculate the accumulation of random variables over time. These three concepts form the foundation of stochastic calculus, and understanding them is essential for applying Shreve stochastic calculus for finance to real-world problems.
How to Apply Shreve’s Stochastic Calculus to Financial Problems
Shreve stochastic calculus for finance provides a powerful framework for analyzing and modeling complex financial systems. By applying Shreve’s stochastic calculus to financial problems, practitioners can gain a deeper understanding of market dynamics and make more informed investment decisions. One of the key applications of Shreve’s stochastic calculus is in modeling stock prices. By using stochastic differential equations, practitioners can capture the random fluctuations of stock prices and estimate their future behavior. Additionally, Shreve’s stochastic calculus can be used to calculate Greeks, such as delta, gamma, and vega, which are essential for risk management and option pricing. Furthermore, Shreve’s stochastic calculus can be applied to estimate risk, allowing practitioners to quantify and manage potential losses. In the context of finance, Shreve stochastic calculus for finance has far-reaching implications, enabling practitioners to develop more accurate models, improve risk management strategies, and optimize portfolio performance.
The Role of Stochastic Calculus in Derivatives Pricing
Derivatives pricing is a critical component of modern finance, and stochastic calculus plays a vital role in this process. The Black-Scholes model, a seminal work in derivatives pricing, relies heavily on stochastic calculus to estimate the value of options and other derivatives. However, the Black-Scholes model has its limitations, such as assuming constant volatility and ignoring other market factors. Shreve stochastic calculus for finance offers a more comprehensive approach to derivatives pricing, allowing for the incorporation of more realistic market assumptions and the estimation of more accurate prices. By applying Shreve’s stochastic calculus, practitioners can better capture the complexities of financial markets, leading to more accurate derivatives pricing and improved risk management. Furthermore, Shreve’s stochastic calculus can be used to develop more sophisticated models, such as the Heston model and the SABR model, which can better capture the dynamics of financial markets. As a result, Shreve stochastic calculus for finance has become an essential tool for derivatives pricing, enabling practitioners to make more informed investment decisions and manage risk more effectively.
Real-World Applications of Stochastic Calculus in Finance
Stochastic calculus, particularly Shreve stochastic calculus for finance, has numerous real-world applications in finance. Investment banks, hedge funds, and asset management firms all utilize stochastic calculus to analyze and manage complex financial systems. For instance, Goldman Sachs uses stochastic calculus to model and price exotic derivatives, while BlackRock employs it to optimize portfolio performance. In addition, stochastic calculus is used in risk management to estimate potential losses and develop strategies to mitigate them. The use of Shreve stochastic calculus for finance has become increasingly prevalent in finance, as it provides a powerful framework for analyzing and modeling complex financial systems. Furthermore, stochastic calculus is used in algorithmic trading to develop high-frequency trading strategies and in credit risk modeling to estimate the likelihood of default. The applications of stochastic calculus in finance are vast and continue to grow, as financial institutions seek to leverage its power to gain a competitive edge.
Overcoming Challenges in Implementing Stochastic Calculus
While Shreve stochastic calculus for finance offers a powerful framework for analyzing and modeling complex financial systems, its implementation can be challenging. One of the primary challenges is data quality issues, as stochastic calculus relies heavily on high-quality data to produce accurate results. Additionally, model risk is a significant concern, as the complexity of stochastic calculus models can make them difficult to interpret and validate. Computational complexity is another challenge, as stochastic calculus models can be computationally intensive, requiring significant processing power and memory. Furthermore, the need for advanced mathematical skills and knowledge of programming languages such as Python or R can create a barrier to entry for some practitioners. To overcome these challenges, it is essential to have a deep understanding of the underlying mathematical concepts, as well as the ability to implement them in a practical setting. By being aware of these challenges and taking steps to address them, practitioners can unlock the full potential of Shreve stochastic calculus for finance and gain a competitive edge in the financial industry.
Best Practices for Mastering Shreve’s Stochastic Calculus
To fully leverage the power of Shreve stochastic calculus for finance, it is essential to develop a deep understanding of its underlying principles and concepts. One of the best practices for mastering Shreve’s stochastic calculus is to start with a solid foundation in probability theory and mathematical statistics. This will provide a strong basis for understanding the advanced mathematical concepts that underlie stochastic calculus. Additionally, practitioners should focus on developing their programming skills, particularly in languages such as Python or R, which are commonly used in finance. This will enable them to implement stochastic calculus models in a practical setting. Furthermore, it is recommended to practice with real-world examples and case studies, such as those found in investment banks, hedge funds, or asset management firms. This will help to develop a deeper understanding of how Shreve’s stochastic calculus can be applied to solve complex financial problems. Finally, staying up-to-date with the latest research and developments in stochastic calculus is crucial, as new applications and techniques are continually emerging. By following these best practices, practitioners can unlock the full potential of Shreve stochastic calculus for finance and gain a competitive edge in the financial industry.
The Future of Stochastic Calculus in Finance
The future of stochastic calculus in finance looks promising, with emerging trends and new applications on the horizon. One area of research that is gaining traction is the use of Shreve stochastic calculus for finance in machine learning and artificial intelligence. By combining stochastic calculus with machine learning algorithms, researchers are developing more accurate and efficient models for predicting stock prices, managing risk, and optimizing portfolios. Another area of growth is the application of stochastic calculus to new financial instruments, such as cryptocurrencies and digital assets. As the financial industry continues to evolve, the importance of Shreve stochastic calculus for finance will only continue to grow. Additionally, advancements in computational power and data storage are enabling researchers to tackle complex problems that were previously unsolvable, leading to new insights and applications of stochastic calculus in finance. Furthermore, the increasing availability of high-quality data and the development of new estimation techniques are allowing for more accurate and reliable models, further solidifying the role of Shreve stochastic calculus for finance in the financial industry. As the field continues to advance, it is likely that stochastic calculus will play an increasingly important role in shaping the future of finance.