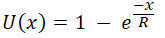Understanding Risk Aversion and Utility
Risk aversion describes an individual’s preference for a certain outcome over a gamble with the same expected value. A risk-averse person will choose a guaranteed lower return instead of a potentially higher but riskier return. This behavior stems from the diminishing marginal utility of wealth. The additional happiness derived from gaining an extra dollar decreases as wealth increases. For example, finding $10 is more impactful when you’re broke than when you’re a millionaire. Utility, in this context, measures the satisfaction or happiness obtained from a given outcome. Understanding this concept is crucial to comprehending the risk averse utility function formula, a tool used to model these preferences mathematically. The formula allows for the quantification of risk aversion, enabling a more precise analysis of decision-making under uncertainty. This quantification is valuable across various fields, including economics and finance. The higher the level of risk aversion, the steeper the curve representing the utility function, highlighting the decreased marginal utility from additional wealth.
Consider a scenario where an individual is offered a choice between receiving $100 with certainty or participating in a gamble with a 50% chance of winning $200 and a 50% chance of winning nothing. A risk-neutral individual would be indifferent between these two options, as the expected value is the same ($100). A risk-averse individual, however, would prefer the certain $100 because the potential loss of anything weighs more heavily on their utility than the potential gain of an equal amount. The risk averse utility function formula provides a quantitative measure of how much more heavily this loss weighs, enabling more accurate prediction of their decisions. This principle applies across various financial decisions. It underpins portfolio optimization, where the goal is to maximize utility given a level of risk. It informs choices about insurance, savings, and investment strategies.
The utility function itself is a mathematical representation of preferences. Different shapes of the utility curve reflect different levels of risk aversion. A linear utility function represents risk neutrality, a concave function represents risk aversion (as shown above), and a convex function represents risk-seeking behavior. The risk averse utility function formula provides a framework for understanding and quantifying this risk aversion, offering valuable insights into how individuals make decisions under uncertainty. Its applications extend beyond personal finance; it finds use in diverse economic models that involve decision-making under uncertainty. The flexibility of the formula and its parameters allows for customization, enabling analysts to account for diverse levels and types of risk aversion across different populations and economic settings. This nuanced application of the formula highlights its robust nature and versatility in diverse contexts.
Visualizing Preferences: The Utility Function Curve
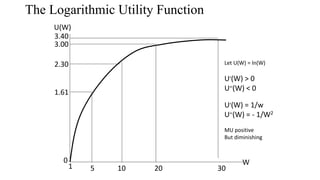
A utility function graphically represents an individual’s preferences. It shows the relationship between wealth or outcomes and the level of utility derived. Utility, in this context, measures the satisfaction or happiness associated with a particular outcome. The shape of the utility function reveals the individual’s attitude towards risk. A risk-averse individual exhibits a concave utility function. This means that the increase in utility diminishes with each additional unit of wealth. The risk-averse utility function formula reflects this diminishing marginal utility. For a risk-neutral individual, the utility function is linear, indicating a constant marginal utility of wealth. Conversely, a convex utility function characterizes a risk-seeking individual, where the marginal utility of wealth increases with each additional unit.
Different types of risk-averse utility functions exist, each with its own characteristics and implications. The constant absolute risk aversion (CARA) model assumes a constant risk aversion level regardless of wealth. The constant relative risk aversion (CRRA) model, on the other hand, assumes that the relative risk aversion remains constant across different wealth levels. Understanding the shape of the utility function is crucial for applying the risk-averse utility function formula accurately. The slope of the curve at any point represents the marginal utility of wealth. A steeper slope indicates higher marginal utility, while a flatter slope suggests lower marginal utility. The curvature reflects the degree of risk aversion. A more pronounced curvature indicates stronger risk aversion. Visualizing these curves helps in understanding how individual preferences influence decisions under uncertainty.
Consider a simple example. Two investment options exist: one with a guaranteed return and another with a higher potential return but also a higher risk. A risk-averse individual, as depicted by their concave utility function and the associated risk-averse utility function formula, would likely choose the guaranteed lower return. This choice reflects the diminishing marginal utility of wealth – the increase in happiness from an extra dollar is less when already wealthy. This preference, illustrated graphically by the utility function, is a direct consequence of the risk-averse utility function formula’s mathematical properties. The formula quantifies the trade-off between risk and return, aligning with the visual representation of the concave curve. This visualization of the risk-averse utility function formula allows for a better understanding of decision-making processes under uncertainty.
Deriving the Formula: A Step-by-Step Approach
This section details the derivation of a common risk-averse utility function formula. A popular choice is the Constant Relative Risk Aversion (CRRA) model. This model assumes that an individual’s relative risk aversion remains constant regardless of their wealth level. The CRRA risk averse utility function formula is defined as U(W) = W(1-γ)/(1-γ) where W represents wealth and γ (gamma) is the coefficient of relative risk aversion. Note that when γ = 1, the formula simplifies to U(W) = ln(W), representing the logarithmic utility function. This is a specific case of the risk averse utility function formula, suitable for situations with a constant relative risk aversion. The derivation begins by considering the properties of a utility function that reflects risk aversion. A risk-averse individual prefers a certain outcome to a gamble with the same expected value. This implies that the utility function is concave, meaning its second derivative is negative. The CRRA model elegantly captures this concavity.
To understand the derivation more deeply, consider the concept of marginal utility. Marginal utility is the additional utility gained from an additional unit of wealth. In a risk-averse utility function formula, marginal utility decreases as wealth increases, reflecting diminishing returns to wealth. Mathematically, this is represented by a negative second derivative. The CRRA model’s parameter, γ, directly controls the degree of this diminishing marginal utility. A higher γ indicates a higher degree of risk aversion, resulting in a steeper decline in marginal utility as wealth increases. Conversely, a lower γ suggests less risk aversion and a gentler decline in marginal utility. The risk averse utility function formula, U(W) = W(1-γ)/(1-γ), encapsulates this relationship effectively. Analyzing this formula reveals the impact of wealth and risk aversion on utility.
Let’s illustrate with an example. Suppose an individual has a CRRA utility function with γ = 2. Their utility function would be U(W) = -1/W. If their wealth doubles from $100 to $200, the increase in utility is readily calculable using the risk averse utility function formula. This increase reflects the individual’s risk aversion. Notice how the increase in utility is less than the proportional increase in wealth, showcasing the diminishing marginal utility inherent in risk aversion. By manipulating the risk averse utility function formula and its parameter γ, one can model various levels of risk aversion, providing a powerful tool for analyzing decision-making under uncertainty. The flexibility of this formula makes it highly valuable in many financial and economic applications. Understanding this formula is crucial for grasping the core principles of risk aversion in decision theory and its applications within portfolio selection and asset pricing.
Analyzing the Parameters: What They Mean and How They Affect Risk Aversion
The risk-averse utility function formula incorporates parameters that significantly influence its shape and, consequently, the level of risk aversion it represents. Understanding these parameters is crucial for correctly interpreting and applying the formula. For instance, in the Constant Relative Risk Aversion (CRRA) model, a common risk-averse utility function formula, a key parameter is the coefficient of relative risk aversion (γ). This coefficient reflects the individual’s sensitivity to changes in wealth relative to their current wealth level. A higher γ indicates a greater degree of risk aversion; the individual requires a larger increase in expected return to compensate for an equivalent increase in risk. Conversely, a lower γ suggests a lower level of risk aversion. The impact of γ on the shape of the risk-averse utility function formula is notable. A higher γ leads to a steeper curve, reflecting a stronger aversion to risk, while a lower γ results in a flatter curve, indicating a weaker aversion to risk. The risk-averse utility function formula, therefore, becomes a powerful tool for modelling individual preferences, when the parameter γ is properly understood and applied.
Another important aspect of the risk-averse utility function formula is its ability to accommodate different types of risk preferences. While the CRRA model focuses on relative risk aversion, the Constant Absolute Risk Aversion (CARA) model utilizes a parameter representing absolute risk aversion. This parameter remains constant regardless of the level of wealth. This means that the individual’s aversion to a specific level of risk does not change based on their wealth. Understanding these nuances helps to determine which risk-averse utility function formula is most appropriate for a given situation. The choice of model depends on the specific assumptions being made and the nature of the decision-making problem under consideration. The correct application of the risk-averse utility function formula is dependent on careful consideration of the model’s parameters and their implications for risk aversion.
Furthermore, it’s important to note that the risk-averse utility function formula is not solely dependent on a single parameter. Other factors, such as the individual’s time preferences and the specific characteristics of the risky outcomes, can also influence the shape and interpretation of the function. Therefore, a complete understanding of the risk-averse utility function formula necessitates considering these additional factors, as well as carefully examining the implications of the chosen parameters. The proper application of the risk-averse utility function formula requires a holistic understanding of its components and their interplay in shaping an individual’s risk preferences. The robustness and accuracy of models using this formula hinge on a precise selection and interpretation of its parameters. Using the risk-averse utility function formula effectively requires a thorough comprehension of these interwoven elements.
Applying the Risk Averse Utility Function Formula: Practical Examples
The risk averse utility function formula finds extensive application in various financial and economic scenarios. Consider a portfolio optimization problem. An investor aims to maximize expected utility, given a set of risky assets with varying returns and volatilities. The risk averse utility function formula allows the investor to quantify the trade-off between expected return and risk. By incorporating the investor’s risk aversion parameter into the formula, one can determine the optimal portfolio allocation that maximizes their utility. This ensures the investor balances potential gains against their aversion to losses. The risk averse utility function formula is crucial here, enabling a mathematically precise approach to portfolio construction tailored to individual risk tolerance.
Another practical application involves pricing risky assets. The formula helps determine a fair price for an asset with uncertain future payoffs. A risk-neutral investor would price the asset based solely on its expected future cash flows. However, a risk-averse investor requires a premium to compensate for the uncertainty involved. This premium is directly related to the level of risk aversion as reflected in the risk averse utility function formula. The higher the risk aversion, the higher the required premium. This is why the risk averse utility function formula is instrumental in models such as the Capital Asset Pricing Model (CAPM), which incorporate risk aversion into asset pricing. The formula provides a concrete way to quantify this risk premium, leading to more accurate asset valuations.
Decision-making under uncertainty frequently utilizes the risk averse utility function formula. Suppose a company faces a choice between two projects: one with a guaranteed moderate return and another with a higher expected return but significant uncertainty. Using the risk averse utility function formula, the company can compare the expected utilities of each project. The formula incorporates the firm’s risk aversion, allowing it to select the project that maximizes its overall utility. This approach ensures decisions are consistent with the company’s risk preferences, leading to more informed and rational choices. The risk averse utility function formula provides a structured framework for evaluating uncertain choices, promoting sound decision-making even under conditions of considerable uncertainty. This demonstrates the wide-ranging applicability of the risk averse utility function formula in practical contexts.
Comparing Different Risk-Averse Utility Functions: Choosing the Right Model
Several risk-averse utility function formulas exist, each with its strengths and weaknesses. The Constant Absolute Risk Aversion (CARA) model assumes a constant risk aversion coefficient, implying that an individual’s willingness to take on risk remains unchanged regardless of their wealth level. This simplifies calculations but may not accurately reflect real-world behavior. The risk-averse utility function formula for CARA is particularly useful in situations where the risk aversion level is constant across different wealth levels. Its simplicity makes it suitable for theoretical analyses and certain applications in finance.
In contrast, the Constant Relative Risk Aversion (CRRA) model assumes that the relative risk aversion remains constant across wealth levels. This implies that the proportion of wealth an individual is willing to risk remains constant, even as their wealth changes. The risk-averse utility function formula for CRRA offers a more nuanced representation of risk preferences, aligning better with observed behavior in many economic contexts. It proves particularly valuable when dealing with situations involving substantial wealth changes, such as long-term investment decisions. The flexibility offered by the CRRA model allows for a more accurate reflection of the dynamic nature of risk aversion in real-world scenarios.
Another commonly used risk-averse utility function formula is the quadratic utility function. This function assumes diminishing marginal utility, reflecting risk aversion. However, it suffers from a potential problem: it can exhibit increasing marginal utility for sufficiently high wealth levels, leading to unrealistic implications. While easy to work with mathematically, the quadratic model’s limitations should be carefully considered before application. The choice between CARA, CRRA, or a quadratic risk-averse utility function formula hinges on the specific context and the desired level of realism. A careful assessment of the underlying assumptions and the implications of each model is crucial for selecting the most appropriate tool for a given problem. The selected risk-averse utility function formula should accurately represent the risk preferences of the decision-maker within the given context.
Dealing with Limitations: Assumptions and Real-World Challenges
The risk averse utility function formula, while a powerful tool for modeling decision-making under uncertainty, relies on several key assumptions. One crucial assumption is the rationality of individuals. The model assumes individuals consistently make choices that maximize their expected utility, given their risk preferences as reflected in the risk averse utility function formula. However, behavioral economics demonstrates that real-world decision-making is often influenced by cognitive biases, such as framing effects or loss aversion, which can lead to deviations from the predictions of the risk averse utility function formula. These biases can systematically distort preferences, resulting in choices inconsistent with the maximization of expected utility.
Another limitation stems from the difficulty in accurately estimating the parameters within the risk averse utility function formula. The risk aversion coefficient, for example, is often difficult to measure empirically. Different elicitation methods can yield different results, leading to uncertainty about the true level of risk aversion for a given individual. Furthermore, the assumption of constant risk aversion, inherent in some commonly used models, may not always be realistic. An individual’s risk tolerance might vary depending on their wealth level or the specific context of the decision. This variability is often not fully captured by the simplified risk averse utility function formula.
Finally, the risk averse utility function formula often simplifies a complex reality. It typically focuses on monetary outcomes, neglecting other factors that influence decision-making, such as social considerations, ethical concerns, or emotional factors. For instance, individuals might make choices that appear inconsistent with their risk aversion preferences when facing decisions with significant emotional consequences. The risk averse utility function formula’s focus on quantifiable outcomes limits its ability to comprehensively model such scenarios. Despite these limitations, the risk averse utility function formula provides a valuable framework for understanding and analyzing decisions under uncertainty. Its continued refinement and the development of more nuanced models will likely lead to a more accurate reflection of real-world behavior.
Advanced Concepts and Further Exploration: Expanding Your Knowledge
Beyond the foundational understanding of the risk averse utility function formula, more nuanced models offer deeper insights into decision-making under uncertainty. Prospect theory, for instance, challenges the expected utility framework by highlighting the influence of framing effects and loss aversion on choices. Individuals may react differently to potential gains and losses, deviating from the predictions of a simple risk averse utility function formula. This theory suggests that the subjective value of an outcome isn’t solely determined by its magnitude but also by its position relative to a reference point.
Stochastic dominance provides a powerful tool for comparing risky prospects without explicitly relying on a specific risk averse utility function formula. It offers a robust way to rank investments based on their probability distributions, identifying those that are unequivocally preferred by all risk-averse individuals. This approach avoids the need to specify a particular functional form for utility, making it a versatile method in portfolio selection and other financial applications. Understanding stochastic dominance complements the use of the risk averse utility function formula, enriching the analytical toolkit for evaluating risk.
Expected utility theory, while foundational to the risk averse utility function formula, presents several limitations. It assumes individuals are perfectly rational and capable of processing complex probabilistic information. However, cognitive biases and bounded rationality often lead to deviations from this idealized model. Exploring advanced topics like ambiguity aversion, where individuals dislike uncertain probabilities, further refines our understanding of risk preferences and the limitations of the risk averse utility function formula in capturing real-world behavior. These advanced concepts provide a richer understanding of individual decision-making beyond the simplified representations of the risk averse utility function formula.