What Drives the Value of Options Contracts
In the world of options trading, understanding the concept of time value is crucial for making informed investment decisions. Time value represents the premium paid for an option beyond its intrinsic value, reflecting the possibility that the option’s value may increase before expiration. This premium is a key driver of the option’s price, and grasping its significance is essential for traders seeking to maximize their returns.
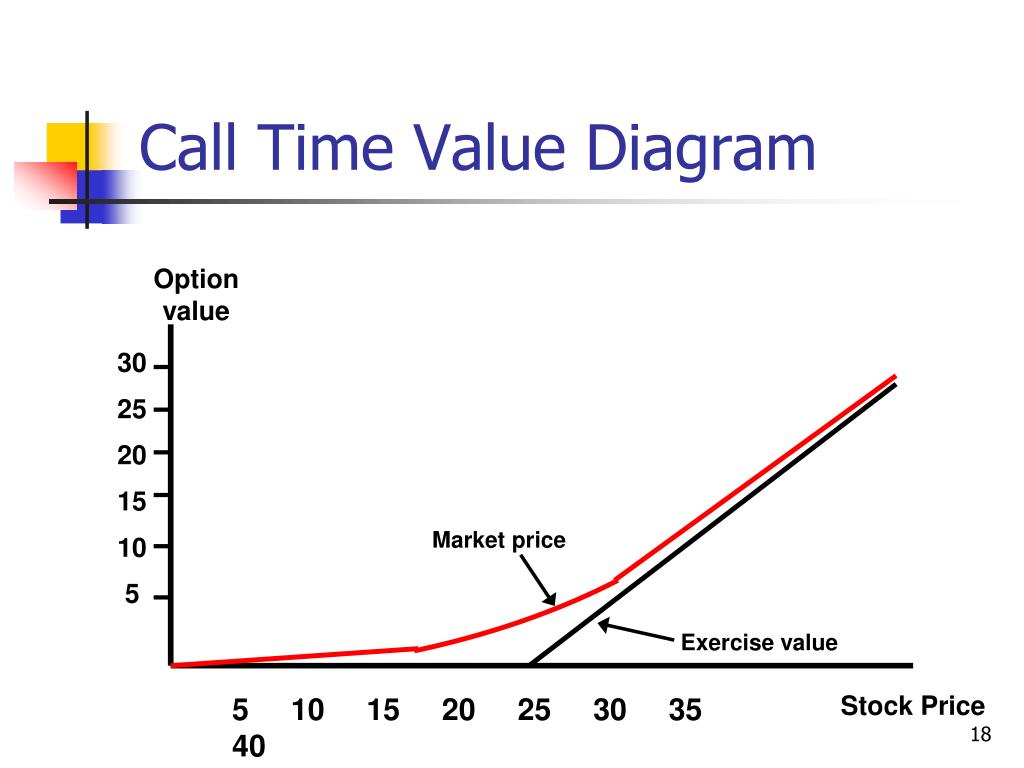
So, what is time value in options? It is the amount by which the option’s price exceeds its intrinsic value, which is the difference between the underlying asset’s price and the option’s strike price. Time value is influenced by several factors, including the underlying asset’s price, volatility, interest rates, and the time remaining until expiration. As these factors fluctuate, the time value of the option adjusts accordingly, affecting its overall price.
Understanding time value is vital for traders, as it helps them determine the fair price of an option and make informed decisions about when to buy or sell. By recognizing the impact of time value on option prices, traders can better navigate the options market and capitalize on market movements.
How to Calculate Time Value in Options
Calculating time value in options is a crucial step in understanding the true worth of an option contract. The time value of an option represents the premium paid for the option beyond its intrinsic value, and it is influenced by several factors, including the underlying asset’s price, volatility, interest rates, and the time remaining until expiration.
The Black-Scholes model is a widely used formula for calculating the time value of an option. The formula is as follows:
Time Value = Call Option Price – Intrinsic Value
Where:
Intrinsic Value = Max (0, Underlying Asset Price – Strike Price)
The variables involved in the Black-Scholes model include:
– Underlying Asset Price: The current market price of the underlying asset.
– Strike Price: The predetermined price at which the option can be exercised.
– Time to Expiration: The amount of time remaining until the option expires.
– Volatility: The expected fluctuation in the underlying asset’s price.
– Risk-Free Interest Rate: The rate of return on a risk-free investment.
For example, let’s say we want to calculate the time value of a call option with a strike price of $50, an underlying asset price of $55, a time to expiration of 30 days, a volatility of 20%, and a risk-free interest rate of 2%. Using the Black-Scholes model, we can calculate the time value of the option as follows:
Time Value = $5.50 (Call Option Price) – $5.00 (Intrinsic Value) = $0.50
In this example, the time value of the option is $0.50, which represents the premium paid for the option beyond its intrinsic value. By understanding how to calculate time value, traders can make more informed decisions about when to buy or sell options, and how to adjust their trading strategies accordingly.
The Role of Expiration Dates in Time Value
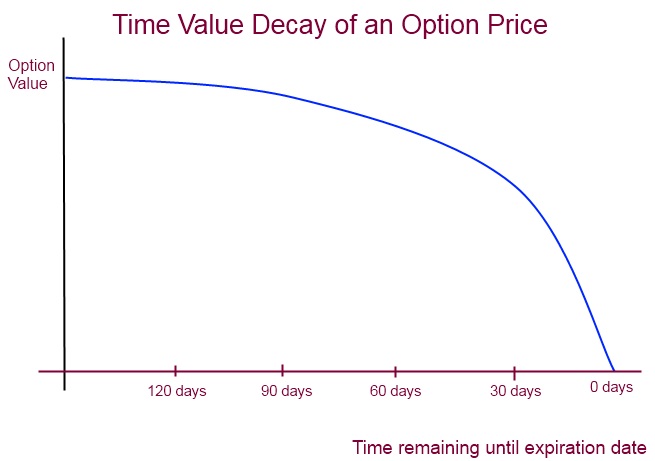
Expiration dates play a critical role in determining the time value of an option. As the expiration date approaches, the time value of the option decreases, and the option’s value becomes more closely tied to its intrinsic value. This phenomenon is known as time decay, and it can have a significant impact on an option’s value.
When an option is far from expiration, the time value is higher, reflecting the possibility that the underlying asset’s price may move in favor of the option holder. As the expiration date draws near, the time value decreases, and the option’s value becomes more dependent on the underlying asset’s current price. This is because there is less time for the underlying asset’s price to move in favor of the option holder.
For example, consider a call option with a strike price of $50 and an underlying asset price of $55. If the option has a year until expiration, the time value may be $5, reflecting the possibility that the underlying asset’s price may increase further. However, if the option has only a month until expiration, the time value may be only $1, as there is less time for the underlying asset’s price to move in favor of the option holder.
The proximity of expiration also affects the option’s sensitivity to changes in the underlying asset’s price. As the expiration date approaches, the option’s delta (a measure of its sensitivity to price changes) increases, making the option more responsive to changes in the underlying asset’s price. This can result in larger profits or losses for the option holder.
Understanding the impact of expiration dates on time value is crucial for traders, as it can help them make informed decisions about when to buy or sell options. By recognizing how time decay affects an option’s value, traders can adjust their trading strategies to maximize their returns.
Understanding the Relationship Between Time Value and Volatility
Volatility plays a crucial role in determining the time value of an option. When volatility increases, the time value of an option also increases, as the option holder has a greater chance of profiting from price movements. Conversely, when volatility decreases, the time value of an option decreases, as the option holder has a lower chance of profiting from price movements.
The relationship between time value and volatility can be attributed to the fact that options are a bet on the uncertainty of the underlying asset’s price. When volatility is high, the uncertainty of the price movement increases, making the option more valuable. This is because the option holder has a greater chance of profiting from large price movements.
For example, consider a call option with a strike price of $50 and an underlying asset price of $55. If the volatility of the underlying asset is high, the time value of the option may be $10, reflecting the high uncertainty of the price movement. However, if the volatility is low, the time value of the option may be only $2, reflecting the lower uncertainty of the price movement.
Traders can take advantage of the relationship between time value and volatility by adjusting their trading strategies accordingly. For instance, when volatility is high, traders may want to buy options with a longer time to expiration, as the time value of the option is higher. Conversely, when volatility is low, traders may want to sell options with a shorter time to expiration, as the time value of the option is lower.
Understanding the relationship between time value and volatility is essential for traders, as it can help them make informed decisions about when to buy or sell options. By recognizing how changes in volatility affect the time value of an option, traders can adjust their trading strategies to maximize their returns and minimize their losses.
The Impact of Interest Rates on Time Value
Interest rates play a significant role in determining the time value of an option. When interest rates rise, the time value of an option decreases, and when interest rates fall, the time value of an option increases. This is because interest rates affect the cost of carrying an option position.
When interest rates are high, the cost of carrying an option position increases, making it more expensive to hold an option. As a result, the time value of the option decreases, as the option holder is less likely to profit from the option. Conversely, when interest rates are low, the cost of carrying an option position decreases, making it less expensive to hold an option. As a result, the time value of the option increases, as the option holder is more likely to profit from the option.
The impact of interest rates on time value can be attributed to the fact that options are a bet on the future price of the underlying asset. When interest rates are high, the future price of the underlying asset is expected to be higher, making the option less valuable. Conversely, when interest rates are low, the future price of the underlying asset is expected to be lower, making the option more valuable.
For example, consider a call option with a strike price of $50 and an underlying asset price of $55. If the interest rate is high, the time value of the option may be $5, reflecting the high cost of carrying the option position. However, if the interest rate is low, the time value of the option may be $10, reflecting the low cost of carrying the option position.
Traders can take advantage of the impact of interest rates on time value by adjusting their trading strategies accordingly. For instance, when interest rates are high, traders may want to sell options with a shorter time to expiration, as the time value of the option is lower. Conversely, when interest rates are low, traders may want to buy options with a longer time to expiration, as the time value of the option is higher.
Understanding the impact of interest rates on time value is essential for traders, as it can help them make informed decisions about when to buy or sell options. By recognizing how changes in interest rates affect the time value of an option, traders can adjust their trading strategies to maximize their returns and minimize their losses.
Time Value and the Greeks: A Deeper Dive
The Greeks, consisting of Delta, Gamma, Theta, and Vega, are essential metrics in options trading that interact with time value to affect trading decisions. Understanding the relationship between time value and the Greeks is crucial for traders to make informed investment decisions.
Delta, which measures the rate of change of the option’s price with respect to the underlying asset‘s price, is closely related to time value. As time value increases, Delta also increases, indicating a higher probability of the option expiring in the money. Conversely, as time value decreases, Delta decreases, indicating a lower probability of the option expiring in the money.
Gamma, which measures the rate of change of Delta, is also affected by time value. As time value increases, Gamma increases, indicating a higher sensitivity of the option’s price to changes in the underlying asset’s price. Conversely, as time value decreases, Gamma decreases, indicating a lower sensitivity of the option’s price to changes in the underlying asset’s price.
Theta, which measures the rate of change of the option’s price with respect to time, is directly related to time value. As time value decreases, Theta increases, indicating a higher rate of time decay. Conversely, as time value increases, Theta decreases, indicating a lower rate of time decay.
Vega, which measures the rate of change of the option’s price with respect to volatility, is also affected by time value. As time value increases, Vega increases, indicating a higher sensitivity of the option’s price to changes in volatility. Conversely, as time value decreases, Vega decreases, indicating a lower sensitivity of the option’s price to changes in volatility.
By understanding the relationship between time value and the Greeks, traders can adjust their trading strategies to maximize their returns and minimize their losses. For instance, traders can use Delta to determine the probability of an option expiring in the money, and adjust their position size accordingly. Similarly, traders can use Gamma to determine the sensitivity of the option’s price to changes in the underlying asset’s price, and adjust their trading strategy accordingly.
In conclusion, the relationship between time value and the Greeks is complex and multifaceted. By understanding how these metrics interact, traders can make more informed investment decisions and achieve consistent trading success.
Real-World Examples of Time Value in Action
To illustrate the practical application of time value in options trading, let’s consider a few real-world examples. These scenarios will demonstrate how traders can use time value concepts to inform their investment decisions and maximize their returns.
Example 1: Buying a Call Option
Suppose a trader buys a call option on a stock with a strike price of $50, expiring in three months. The current market price of the stock is $45, and the trader expects the price to rise to $60 in the next three months. The time value of the option is $5, reflecting the probability of the stock price reaching $60 by expiration. If the trader is correct, and the stock price reaches $60, the option will expire in the money, and the trader can exercise the option to buy the stock at $50, selling it at $60 for a profit of $10.
Example 2: Selling a Put Option
Consider a trader who sells a put option on a stock with a strike price of $40, expiring in two months. The current market price of the stock is $45, and the trader expects the price to remain stable or rise in the next two months. The time value of the option is $3, reflecting the probability of the stock price falling below $40 by expiration. If the trader is correct, and the stock price remains above $40, the option will expire out of the money, and the trader can keep the premium received for selling the option.
Example 3: Time Value and Volatility
Suppose a trader buys a call option on a stock with a strike price of $50, expiring in six months. The current market price of the stock is $45, and the trader expects the price to rise to $60 in the next six months. However, the trader also expects volatility to increase in the next six months, which will increase the time value of the option. If volatility does increase, the time value of the option will increase, making the option more valuable. The trader can then sell the option at a higher price, locking in a profit.
These examples illustrate how time value can be used in various options trading strategies. By understanding the concept of time value and its relationship with other factors such as volatility and interest rates, traders can make more informed investment decisions and maximize their returns.
Mastering Time Value for Consistent Trading Success
In conclusion, understanding time value is crucial for options traders seeking to maximize their returns and minimize their losses. By grasping the concept of time value and its relationships with other factors such as volatility, interest rates, and the Greeks, traders can make more informed investment decisions and develop effective trading strategies.
Key takeaways from this article include the importance of considering time value when evaluating options contracts, the impact of expiration dates on time value, and the role of volatility and interest rates in affecting time value. Additionally, understanding the relationship between time value and the Greeks can help traders optimize their trading decisions and manage risk more effectively.
To incorporate time value into a trading plan, traders should consider the following strategies:
- Monitor time value and adjust trading decisions accordingly, taking into account the proximity of expiration and changes in volatility and interest rates.
- Use the Greeks to gauge the sensitivity of options prices to changes in underlying factors and adjust position sizes and trading strategies accordingly.
- Consider selling options with high time value to capitalize on the premium received, and buying options with low time value to benefit from potential price movements.
By mastering the concept of time value and its applications in options trading, traders can gain a competitive edge in the markets and achieve consistent trading success. Remember, what is time value in options? It is the key to unlocking profitable trading opportunities and minimizing losses in the complex world of options trading.