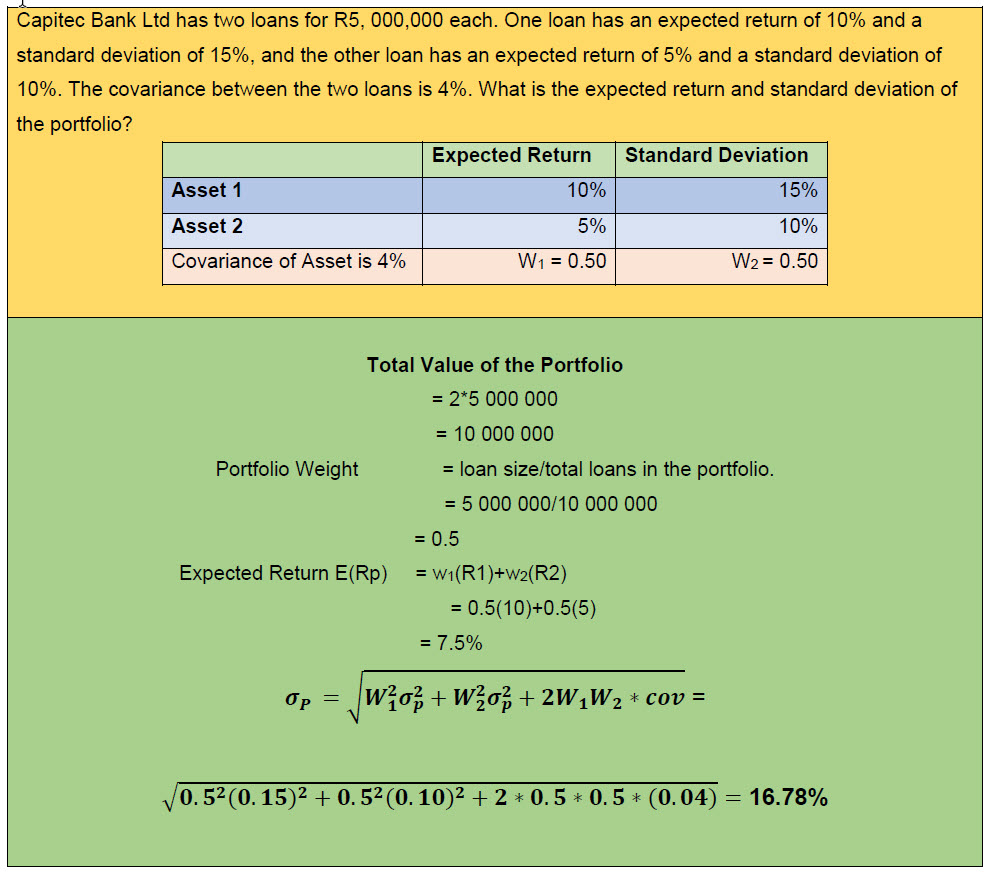
What is Portfolio Standard Deviation?
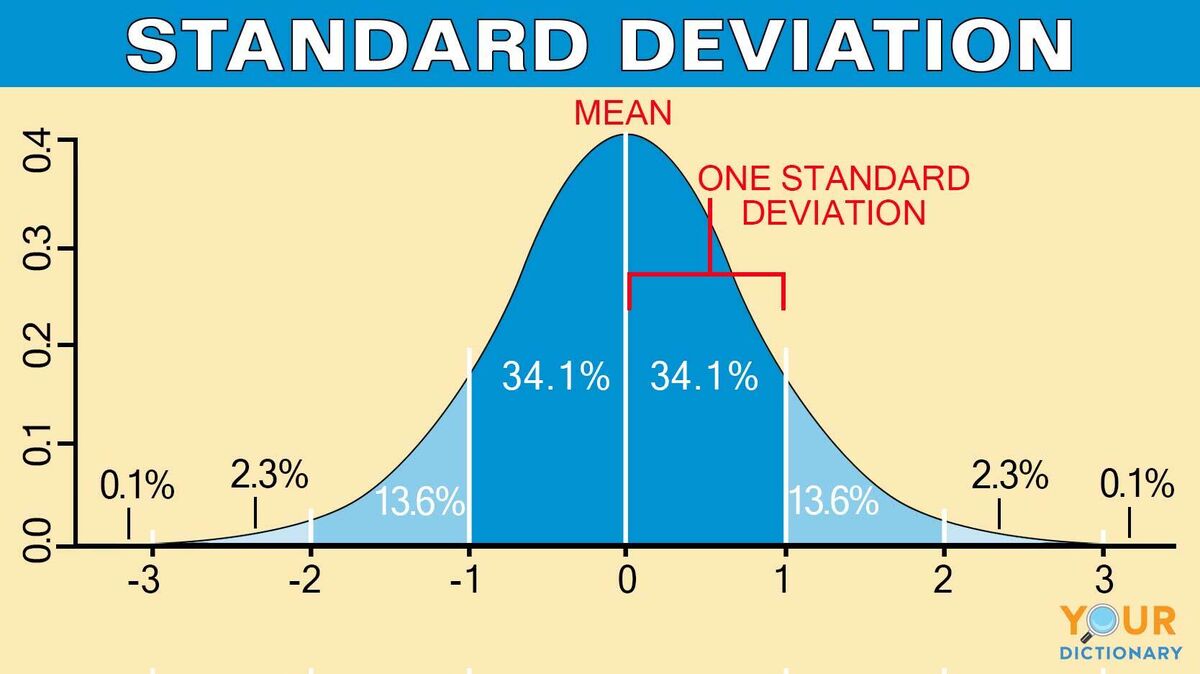
Portfolio standard deviation is a statistical measurement that quantifies the risk or volatility associated with the returns of a portfolio. It is calculated by taking the square root of the variance of the portfolio’s returns, which measures the dispersion of returns around an average value. Variance, in turn, is calculated by finding the average of the squared differences between each return and the mean return.
The standard deviation of a portfolio is expressed in the same units as the returns, making it an intuitive and easily interpretable measure of risk. A higher standard deviation indicates greater volatility and risk, while a lower standard deviation suggests more stability and predictability in the portfolio’s returns. By measuring the dispersion of returns, portfolio standard deviation helps investors assess the likelihood of experiencing both positive and negative returns relative to the portfolio’s average return.
In portfolio management, standard deviation is a crucial metric for investors seeking to balance risk and return. By understanding the standard deviation of a portfolio, investors can make informed decisions about the level of risk they are willing to assume and the potential rewards they can expect. This, in turn, enables them to construct portfolios that align with their investment goals, risk tolerance, and time horizon.
Importance of Portfolio Standard Deviation
Portfolio standard deviation is a critical metric for investors seeking to assess the risk level of their portfolios and make informed investment decisions. By measuring the dispersion of returns around an average value, portfolio standard deviation provides investors with a quantitative measure of risk that can help them evaluate the potential volatility of their investments.
Understanding the standard deviation of a portfolio is essential for several reasons. First, it enables investors to assess the likelihood of experiencing both positive and negative returns relative to the portfolio’s average return. This, in turn, can help investors determine whether the expected returns of a portfolio are commensurate with the level of risk they are willing to assume.
Second, portfolio standard deviation can help investors compare different investment options and make informed decisions about which portfolios align with their investment goals and risk tolerance. By comparing the standard deviations of different portfolios, investors can identify those that offer the best balance of risk and return, taking into account their individual preferences and circumstances.
Third, portfolio standard deviation can help investors monitor the performance of their portfolios over time and make adjustments as necessary. By tracking the standard deviation of a portfolio, investors can identify changes in the portfolio’s risk profile and take action to mitigate any unexpected volatility or risk.
In summary, portfolio standard deviation is a crucial metric for investors seeking to manage risk and make informed investment decisions. By understanding the concept of portfolio standard deviation and how it is calculated, investors can use this metric to assess the risk level of their portfolios, compare different investment options, and monitor the performance of their investments over time.
How to Calculate Portfolio Standard Deviation
Calculating the standard deviation of a portfolio involves several steps, which are outlined below:
- Calculate the variance of individual assets: The first step in calculating portfolio standard deviation is to calculate the variance of each individual asset in the portfolio. Variance is a measure of the dispersion of returns around an average value and is calculated by finding the average of the squared differences between each return and the mean return.
- Weight the assets according to their proportions in the portfolio: Once the variance of each individual asset has been calculated, the next step is to weight each asset according to its proportion in the portfolio. This is because the contribution of each asset to the overall risk of the portfolio depends on its relative size or weight.
- Calculate the covariance between each pair of assets: Covariance is a measure of the degree to which two variables move together. In the context of portfolio management, covariance is used to quantify the relationship between the returns of different assets in the portfolio. Specifically, the covariance between each pair of assets is calculated and used to determine the extent to which the returns of one asset are correlated with the returns of another asset.
- Calculate the variance of the portfolio: Once the variance of each individual asset and the covariance between each pair of assets have been calculated, the variance of the portfolio can be calculated using the formula:
Variance of the portfolio = weight1^2 \* variance of asset 1 + weight2^2 \* variance of asset 2 + 2 \* weight1 \* weight2 \* covariance between asset 1 and asset 2
- Calculate the standard deviation of the portfolio: Finally, the standard deviation of the portfolio can be calculated by taking the square root of the variance of the portfolio. The resulting value represents the risk or volatility associated with the portfolio’s returns.
By following these steps, investors can calculate the standard deviation of their portfolio and use this metric to assess the risk level of their investments. It is important to note, however, that portfolio standard deviation is just one measure of risk and should be used in conjunction with other metrics to provide a more complete picture of portfolio risk.
Comparing Portfolio Standard Deviations
Comparing the standard deviations of different portfolios can help investors make informed decisions about which portfolios align with their investment goals and risk tolerance. By comparing the standard deviations of different portfolios, investors can identify those that offer the best balance of risk and return, taking into account their individual preferences and circumstances.
When comparing the standard deviations of different portfolios, it is important to consider the concept of risk tolerance. Risk tolerance refers to an investor’s willingness and ability to assume risk in pursuit of higher returns. Investors with a high risk tolerance may be more comfortable with portfolios that have higher standard deviations, while investors with a low risk tolerance may prefer portfolios with lower standard deviations.
For example, an investor with a high risk tolerance may be willing to invest in a portfolio with a standard deviation of 15%, recognizing that this portfolio may experience significant fluctuations in value over time. In contrast, an investor with a low risk tolerance may prefer a portfolio with a standard deviation of 5%, even if this means accepting lower potential returns.
When comparing the standard deviations of different portfolios, it is also important to consider the potential impact of extreme events or “black swan” events. While portfolio standard deviation is a useful measure of risk, it does not account for the possibility of extreme events that can have a significant impact on portfolio performance. As such, investors should use portfolio standard deviation in conjunction with other risk metrics, such as value at risk or expected shortfall, to provide a more complete picture of portfolio risk.
In summary, comparing the standard deviations of different portfolios can help investors make informed decisions about which portfolios align with their investment goals and risk tolerance. By understanding the concept of risk tolerance and using portfolio standard deviation in conjunction with other risk metrics, investors can construct portfolios that balance risk and return in a way that meets their individual needs and preferences.
Strategies to Reduce Portfolio Standard Deviation
Reducing portfolio standard deviation is an important consideration for investors seeking to manage risk and achieve their investment goals. There are several strategies that investors can use to reduce portfolio standard deviation, including:
- Diversification: Diversification involves spreading investments across a range of assets, sectors, and geographic regions. By investing in a diversified portfolio, investors can reduce their exposure to individual assets or sectors and thereby reduce portfolio standard deviation.
- Investing in low-volatility assets: Low-volatility assets, such as government bonds or dividend-paying stocks, tend to have lower standard deviations than higher-risk assets, such as equities or derivatives. By investing in low-volatility assets, investors can reduce portfolio standard deviation while still achieving their investment goals.
- Hedging strategies: Hedging strategies involve using financial instruments, such as options or futures, to reduce the impact of adverse market movements on a portfolio. By using hedging strategies, investors can reduce portfolio standard deviation and manage risk more effectively.
- Risk management tools: There are several risk management tools, such as stop-loss orders or position sizing, that investors can use to reduce portfolio standard deviation. By using these tools, investors can limit their exposure to individual assets or sectors and thereby reduce portfolio standard deviation.
It is important to note that reducing portfolio standard deviation should be balanced against the need to achieve investment goals. Investors should aim to construct portfolios that balance risk and return in a way that meets their individual needs and preferences. This may involve accepting a higher level of risk in pursuit of higher returns or accepting a lower level of risk in order to preserve capital.
In summary, reducing portfolio standard deviation is an important consideration for investors seeking to manage risk and achieve their investment goals. By diversifying investments, investing in low-volatility assets, using hedging strategies, and employing risk management tools, investors can reduce portfolio standard deviation and manage risk more effectively. However, it is important to balance the need to reduce portfolio standard deviation against the need to achieve investment goals, and investors should construct portfolios that balance risk and return in a way that meets their individual needs and preferences.
Limitations of Portfolio Standard Deviation
While portfolio standard deviation is a useful measure of risk, it is important to recognize its limitations as a measure of portfolio risk. Specifically, portfolio standard deviation does not account for the following factors:
- Skewness: Skewness refers to the degree to which the distribution of returns is asymmetric. A positively skewed distribution has a longer right tail, indicating a higher likelihood of large positive returns, while a negatively skewed distribution has a longer left tail, indicating a higher likelihood of large negative returns. Portfolio standard deviation does not account for skewness and may not accurately reflect the true risk profile of a portfolio.
- Kurtosis: Kurtosis refers to the degree to which the distribution of returns is “fat-tailed” or “thin-tailed.” A distribution with high kurtosis has a higher likelihood of extreme events, while a distribution with low kurtosis has a lower likelihood of extreme events. Portfolio standard deviation does not account for kurtosis and may not accurately reflect the true risk profile of a portfolio, particularly in the presence of extreme events.
- Extreme events: Portfolio standard deviation is calculated based on historical returns and may not accurately reflect the risk of extreme events that have not occurred in the past. As such, portfolio standard deviation may underestimate the true risk profile of a portfolio, particularly in the presence of “black swan” events that have a low probability of occurrence but can have a significant impact on portfolio performance.
Given these limitations, it is important for investors to use portfolio standard deviation in conjunction with other risk metrics, such as value at risk or expected shortfall, to provide a more complete picture of portfolio risk. By using a range of risk metrics, investors can better understand the true risk profile of their portfolios and make informed investment decisions that align with their risk tolerance and investment goals.
In summary, while portfolio standard deviation is a useful measure of risk, it has several limitations that investors should be aware of. Specifically, portfolio standard deviation does not account for skewness, kurtosis, or extreme events and may not accurately reflect the true risk profile of a portfolio. To provide a more complete picture of portfolio risk, investors should use portfolio standard deviation in conjunction with other risk metrics and consider a range of factors when making investment decisions.
Portfolio Standard Deviation vs. Other Risk Metrics
While portfolio standard deviation is a useful measure of risk, it is not the only risk metric available to investors. Other risk metrics, such as value at risk, expected shortfall, and conditional value at risk, can provide additional insights into the risk profile of a portfolio. In this section, we will compare portfolio standard deviation to these other risk metrics and discuss the advantages and disadvantages of each metric.
Value at Risk (VaR)
Value at risk (VaR) is a statistical measure that quantifies the potential loss in the value of a portfolio over a given time horizon at a given confidence level. For example, a VaR of $1 million at a 95% confidence level over a one-month horizon indicates that there is a 5% probability that the portfolio will lose more than $1 million over the next month.
VaR is a useful risk metric because it provides a clear and concise measure of potential losses. However, it has several limitations. Specifically, VaR does not provide information about the severity of losses beyond the VaR threshold, and it may underestimate the true risk profile of a portfolio in the presence of extreme events.
Expected Shortfall (ES)
Expected shortfall (ES) is a risk metric that builds upon VaR by quantifying the expected loss in the value of a portfolio beyond the VaR threshold. For example, an ES of $2 million at a 95% confidence level over a one-month horizon indicates that, in the worst 5% of cases, the portfolio is expected to lose an average of $2 million over the next month.
ES is a useful risk metric because it provides information about the severity of losses beyond the VaR threshold. However, it has several limitations. Specifically, ES is more complex and difficult to calculate than VaR, and it may be sensitive to the choice of confidence level and time horizon.
Conditional Value at Risk (CVaR)
Conditional value at risk (CVaR) is a risk metric that is similar to ES but is calculated differently. Specifically, CVaR is calculated as the average of the VaR values in the worst 5% of cases, rather than the expected loss in the worst 5% of cases. For example, a CVaR of $2 million at a 95% confidence level over a one-month horizon indicates that, on average, the portfolio is expected to lose $2 million in the worst 5% of cases over the next month.
CVaR is a useful risk metric because it provides information about the severity of losses beyond the VaR threshold. However, it has several limitations. Specifically, CVaR is more complex and difficult to calculate than VaR, and it may be sensitive to the choice of confidence level and time horizon.
Advantages and Disadvantages of Portfolio Standard Deviation
Portfolio standard deviation has several advantages as a risk metric. Specifically, it is easy to calculate, widely understood, and provides information about the volatility of portfolio returns. However, it has several limitations, as discussed in a previous section. To provide a more complete picture of portfolio risk, investors should consider using a range of risk metrics, including portfolio standard deviation, VaR, ES, and CVaR, and should balance the advantages and disadvantages of each metric when making investment decisions.
In summary, while portfolio standard deviation is a useful measure of risk, it is not the only risk metric available to investors. Other risk metrics, such as VaR, ES, and CVaR, can provide additional insights into the risk profile of a portfolio. By using a range of risk metrics and balancing the advantages and disadvantages of each metric, investors can better understand the true risk profile of their portfolios and make informed investment decisions that align with their risk tolerance and investment goals.
Real-World Examples of Portfolio Standard Deviation
Portfolio standard deviation is a widely used risk metric in the investment management industry. Here are some real-world examples of how it has been used in practice to inform investment decisions and manage portfolio risk:
Example 1: Diversification
Consider a portfolio consisting of two assets: Stock A and Stock B. The expected returns and standard deviations of the two assets are as follows:
- Stock A: Expected return = 10%, Standard deviation = 15%
- Stock B: Expected return = 15%, Standard deviation = 25%
By diversifying the portfolio equally between the two assets, the portfolio standard deviation can be calculated as follows:
- Portfolio variance = (0.5^2 \* 0.15^2) + (0.5^2 \* 0.25^2) + 2 \* (0.5 \* 0.5) \* 0.5 \* 0.15 \* 0.25 \* 0.5 = 0.022125
- Portfolio standard deviation = sqrt(0.022125) = 0.1487 or 14.87%
By diversifying the portfolio, the portfolio standard deviation has been reduced from the weighted average of the individual asset standard deviations (20%) to 14.87%. This example illustrates the benefits of diversification in reducing portfolio risk.
Example 2: Low-Volatility Assets
Consider a portfolio consisting of two assets: Stock C and a bond. The expected returns and standard deviations of the two assets are as follows:
- Stock C: Expected return = 8%, Standard deviation = 20%
- Bond: Expected return = 4%, Standard deviation = 5%
By investing 50% of the portfolio in Stock C and 50% in the bond, the portfolio standard deviation can be calculated as follows:
- Portfolio variance = (0.5^2 \* 0.20^2) + (0.5^2 \* 0.05^2) + 2 \* (0.5 \* 0.5) \* 0.5 \* 0.20 \* 0.05 = 0.0125
- Portfolio standard deviation = sqrt(0.0125) = 0.1118 or 11.18%
By investing in a low-volatility asset such as a bond, the portfolio standard deviation has been reduced from 20% to 11.18%. This example illustrates the benefits of investing in low-volatility assets in reducing portfolio risk.
Example 3: Hedging Strategies
Consider a portfolio consisting of a stock and a put option on the same stock. The expected returns and standard deviations of the two assets are as follows:
- Stock: Expected return = 10%, Standard deviation = 20%
- Put option: Expected return = -2%, Standard deviation = 15%
By using a put option as a hedging strategy, the portfolio standard deviation can be calculated as follows:
- Portfolio variance = (0.5^2 \* 0.20^2) + (0.5^2 \* 0.15^2) + 2 \* (0.5 \* 0.5) \* 0.5 \* 0.20 \* 0.15 \* (-1) = 0.0175
- Portfolio standard deviation = sqrt(0.0175) = 0.1323 or 13.23%
By using a put option as a hedging strategy, the portfolio standard deviation has been reduced from 20% to 13.23%. This example illustrates the benefits of hedging strategies in reducing portfolio risk.
In summary, portfolio standard deviation is a widely used risk metric in the investment management industry. By diversifying investments, investing in low-volatility assets, and using hedging strategies, investors can reduce portfolio standard deviation and manage portfolio risk. Real-world examples of portfolio standard deviation in action include diversification, low-volatility assets, and hedging strategies. By understanding the concept of portfolio standard deviation and how it can be used in practice, investors can make informed investment decisions that align with their risk tolerance and investment goals.