Understanding the Concept of Standard Deviation in Finance
In the world of finance, standard deviation is a crucial metric that helps investors and portfolio managers quantify the volatility of their investments. It is a statistical measure that calculates the dispersion of a set of values from their mean value. In portfolio management, standard deviation is used to assess the risk associated with a particular investment or a portfolio of investments. A higher standard deviation indicates a higher level of risk, while a lower standard deviation suggests a more stable investment. By understanding standard deviation, investors can make informed decisions about their investments, balancing risk and potential returns. The ability to calculate standard deviation using the standard deviation formula for portfolio is essential in this regard, enabling investors to quantify and manage risk effectively. This metric is particularly useful in portfolio optimization, where it helps investors balance risk and return, leading to more consistent returns.
How to Calculate Standard Deviation for a Portfolio: A Step-by-Step Approach
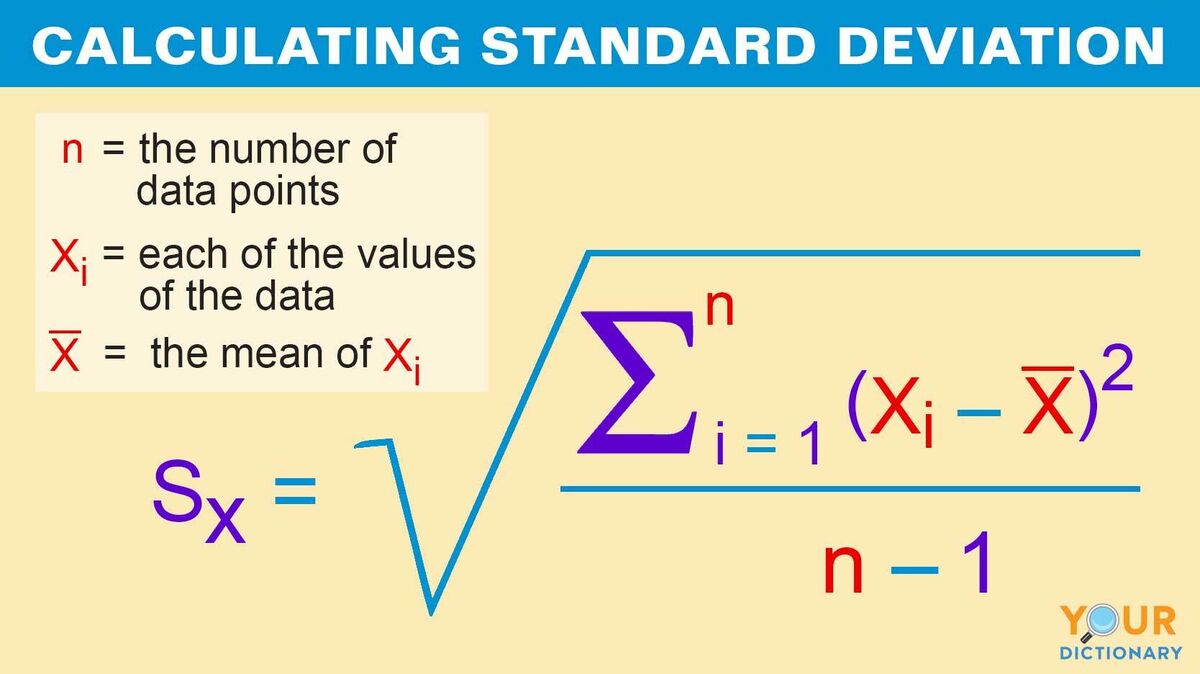
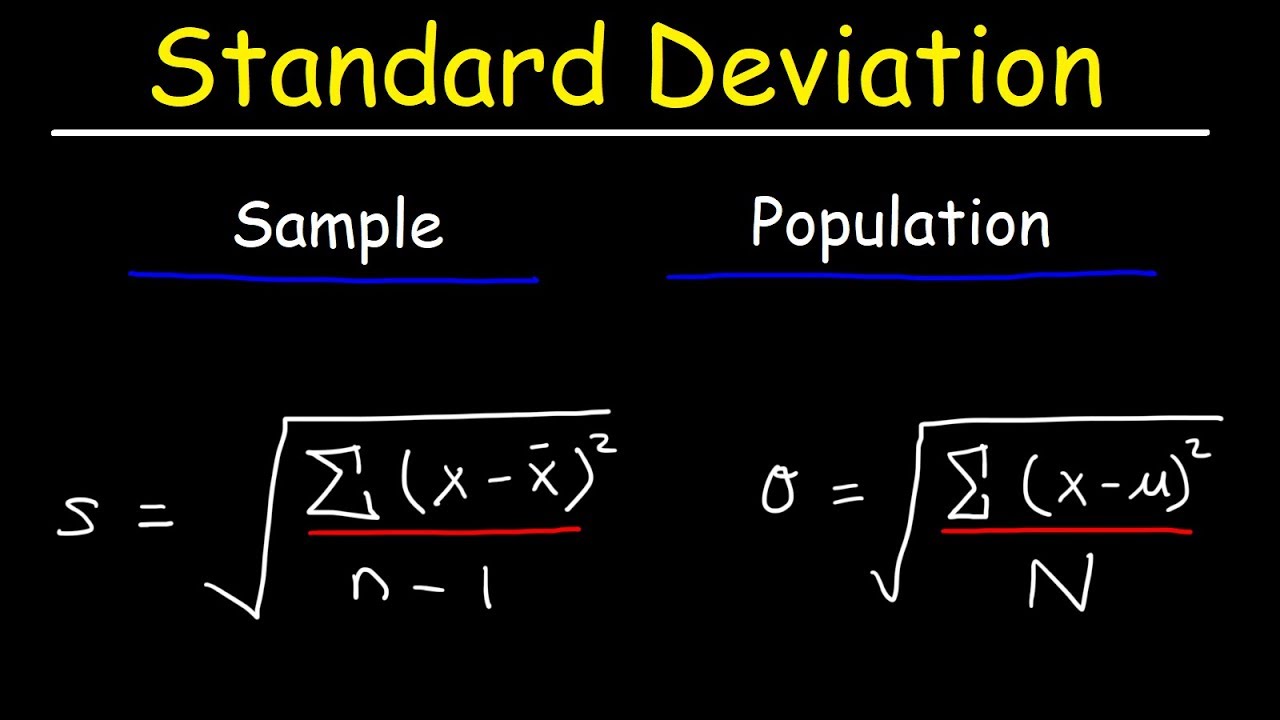
To calculate the standard deviation of a portfolio, investors can follow a step-by-step approach using the standard deviation formula for portfolio. The formula is: σ = √(Σ(xi – μ)^2 / (n – 1)), where σ is the standard deviation, xi is each data point, μ is the mean return, and n is the number of data points. Here’s a breakdown of each component:
1. Mean Return (μ): Calculate the average return of the portfolio over a specified period. This can be done by summing up all the returns and dividing by the number of data points.
2. Squared Deviations: Calculate the squared difference between each data point and the mean return. This is done by subtracting the mean return from each data point and squaring the result.
3. Sum of Squared Deviations: Add up all the squared deviations calculated in step 2.
4. Divide by (n – 1): Divide the sum of squared deviations by the number of data points minus one.
5. Take the Square Root: Take the square root of the result obtained in step 4 to get the standard deviation.
By following these steps, investors can calculate the standard deviation of their portfolio using the standard deviation formula for portfolio, which is essential in measuring portfolio risk and volatility.
The Importance of Standard Deviation in Portfolio Optimization
In portfolio optimization, standard deviation plays a crucial role in helping investors balance risk and return. By calculating the standard deviation of a portfolio using the standard deviation formula for portfolio, investors can gain valuable insights into the portfolio’s volatility and risk profile. A lower standard deviation indicates a more stable portfolio with less volatility, while a higher standard deviation suggests a riskier portfolio with greater potential for losses.
A key benefit of standard deviation in portfolio optimization is its ability to help investors achieve more consistent returns. By minimizing standard deviation, investors can reduce the likelihood of extreme losses and gains, resulting in a more stable investment portfolio. This is particularly important for investors with a low-risk tolerance or those seeking to preserve their capital.
In addition, standard deviation can be used to optimize portfolio construction by identifying the most efficient asset allocation. By analyzing the standard deviation of different asset classes and securities, investors can create a diversified portfolio that balances risk and return. This can involve allocating a larger proportion of the portfolio to low-volatility assets, such as bonds, and a smaller proportion to high-volatility assets, such as stocks.
Furthermore, standard deviation can be used to evaluate the performance of different investment strategies and managers. By comparing the standard deviation of different portfolios or investment strategies, investors can identify those that are most effective in managing risk and achieving consistent returns.
In conclusion, standard deviation is a critical component of portfolio optimization, enabling investors to balance risk and return, achieve more consistent returns, and optimize portfolio construction. By mastering the standard deviation formula for portfolio and understanding its importance in portfolio optimization, investors can make more informed investment decisions and achieve their financial goals.
Interpreting Standard Deviation Results: What Do the Numbers Mean?
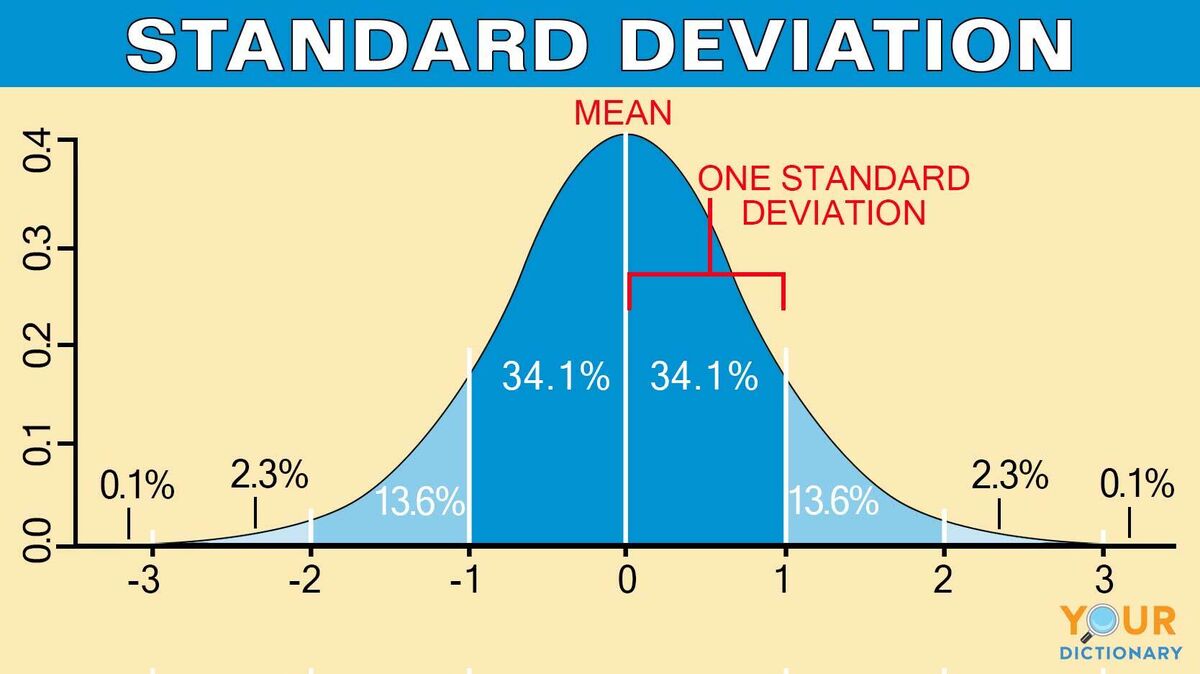
Once the standard deviation of a portfolio has been calculated using the standard deviation formula for portfolio, it’s essential to understand what the results mean in terms of portfolio risk and volatility. A high standard deviation indicates a riskier portfolio with a higher potential for losses, while a low standard deviation suggests a more stable portfolio with less volatility.
A standard deviation of 10%, for example, means that there is a 68% probability that the portfolio’s return will fall within a range of 10% above or below the mean return. This information can be used to make informed investment decisions, such as adjusting the asset allocation or diversifying the portfolio to reduce risk.
In addition, standard deviation can be used to evaluate the performance of different investment strategies and managers. By comparing the standard deviation of different portfolios or investment strategies, investors can identify those that are most effective in managing risk and achieving consistent returns.
For instance, a portfolio with a standard deviation of 8% may be considered more attractive than one with a standard deviation of 12%, as it suggests a lower level of risk and volatility. However, it’s essential to consider other factors, such as the portfolio’s expected return and investment objectives, when making investment decisions.
Furthermore, standard deviation can be used to set risk tolerance levels and establish stop-loss limits. By setting a maximum acceptable standard deviation, investors can limit their exposure to risk and avoid significant losses.
In conclusion, interpreting the results of the standard deviation calculation is crucial in understanding portfolio risk and volatility. By understanding what the numbers mean, investors can make informed investment decisions, adjust their asset allocation, and optimize their portfolio’s performance.
Comparing Standard Deviation with Other Risk Metrics: A Comprehensive Analysis
In addition to standard deviation, there are several other risk metrics that investors use to measure portfolio risk and volatility. Two commonly used metrics are value-at-risk (VaR) and beta. While each of these metrics provides valuable insights into portfolio risk, they have different strengths and limitations.
VaR, for example, measures the potential loss of a portfolio over a specific time horizon with a given probability. It is often used to set risk limits and determine capital requirements. However, VaR has some limitations, such as assuming a normal distribution of returns and not capturing tail risk.
Beta, on the other hand, measures the systematic risk of a portfolio relative to the overall market. A beta of 1 indicates that the portfolio moves in line with the market, while a beta greater than 1 indicates higher volatility. However, beta does not capture idiosyncratic risk and may not be suitable for portfolios with non-normal return distributions.
In contrast, standard deviation provides a comprehensive measure of portfolio risk and volatility, capturing both systematic and idiosyncratic risk. It is also a more intuitive metric, allowing investors to easily understand the potential range of returns. However, standard deviation has its own limitations, such as assuming a normal distribution of returns and not capturing tail risk.
When to use each metric depends on the investment objectives and risk tolerance of the investor. VaR is suitable for investors who want to set risk limits and determine capital requirements, while beta is useful for investors who want to measure systematic risk. Standard deviation, on the other hand, provides a comprehensive measure of portfolio risk and volatility, making it a useful metric for investors who want to optimize their portfolio’s performance.
In conclusion, each risk metric has its strengths and limitations, and investors should use a combination of metrics to get a comprehensive view of portfolio risk and volatility. By understanding the differences between standard deviation, VaR, and beta, investors can make more informed investment decisions and optimize their portfolio’s performance.
Real-World Applications of Standard Deviation in Portfolio Management
In the real world, standard deviation plays a critical role in portfolio management, informing investment decisions and risk management strategies. Many investment firms and financial institutions use standard deviation to measure and manage portfolio risk, ensuring that their investments align with their risk tolerance and investment objectives.
For example, a pension fund may use standard deviation to determine the optimal asset allocation for its portfolio, balancing risk and return to ensure that it meets its long-term obligations. By calculating the standard deviation of different asset classes, the fund can identify the most volatile assets and adjust its allocation accordingly.
In addition, standard deviation is used in risk parity strategies, which aim to balance risk across different asset classes. By calculating the standard deviation of each asset class, investors can allocate their portfolio to achieve a consistent level of risk across all assets.
Standard deviation is also used in portfolio optimization techniques, such as mean-variance optimization. This approach involves calculating the standard deviation of a portfolio and then optimizing the portfolio to achieve the highest return for a given level of risk.
Furthermore, standard deviation is used in performance measurement and attribution, helping investors to evaluate the performance of their portfolio and identify areas for improvement. By calculating the standard deviation of a portfolio’s returns, investors can determine whether their portfolio is meeting its investment objectives and adjust their strategy accordingly.
In conclusion, standard deviation is a widely used metric in portfolio management, informing investment decisions and risk management strategies. By understanding how to calculate and interpret standard deviation, investors can make more informed decisions and optimize their portfolio’s performance.
Common Mistakes to Avoid When Calculating Standard Deviation for a Portfolio
When calculating standard deviation for a portfolio, investors often make mistakes that can lead to inaccurate results and poor investment decisions. To avoid these mistakes, it’s essential to understand the common pitfalls and take steps to mitigate them.
One common mistake is using incorrect or incomplete data. This can include using historical returns that are not representative of the portfolio’s current composition or using data that is not adjusted for dividends or inflation. To avoid this mistake, investors should ensure that they are using accurate and up-to-date data that reflects the portfolio’s current composition.
Another mistake is misunderstanding the standard deviation formula for portfolio. This can include incorrectly calculating the mean return or squared deviations, or failing to account for the portfolio’s covariance. To avoid this mistake, investors should carefully review the formula and ensure that they are applying it correctly.
In addition, investors may fail to consider the time period over which they are calculating standard deviation. This can lead to inaccurate results, as standard deviation can vary significantly over different time periods. To avoid this mistake, investors should ensure that they are using a consistent time period and adjusting for any seasonal or cyclical fluctuations.
Furthermore, investors may fail to consider the impact of correlations between assets on standard deviation. This can lead to an underestimation of portfolio risk, as correlations can increase the overall volatility of the portfolio. To avoid this mistake, investors should ensure that they are accounting for correlations between assets and adjusting their standard deviation calculation accordingly.
By avoiding these common mistakes, investors can ensure that they are accurately calculating standard deviation and making informed investment decisions. By understanding the importance of accurate data, correct formula application, and consideration of correlations and time periods, investors can optimize their portfolio’s performance and achieve their investment objectives.
Conclusion: Mastering Standard Deviation for Informed Investment Decisions
In conclusion, standard deviation is a crucial concept in portfolio risk management, providing investors with a quantitative measure of portfolio volatility. By understanding how to calculate and interpret standard deviation, investors can make more informed decisions about their investments. The standard deviation formula for portfolio calculation is a powerful tool that helps investors balance risk and return, and its importance cannot be overstated. By avoiding common mistakes and mastering the concept of standard deviation, investors can create a more diversified portfolio that aligns with their risk tolerance and investment goals. Ultimately, a deep understanding of standard deviation is essential for achieving long-term investment success.