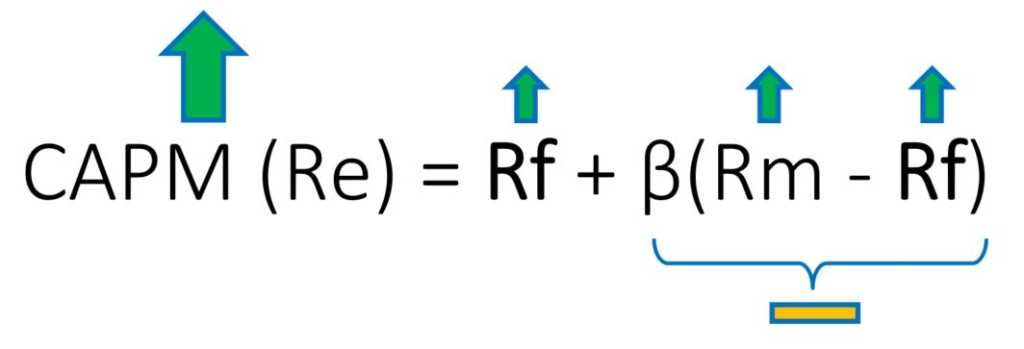Understanding the Concept of the Real Risk-Free Rate
The real risk-free rate of return represents the return an investor expects from a completely risk-free investment, after accounting for inflation. This crucial concept differs significantly from the nominal risk-free rate, often represented by the yield on a government bond. The nominal rate reflects the raw return without adjusting for inflation’s eroding effect on purchasing power. The real risk-free rate provides a clearer picture of the investment’s true return. For example, a government bond yielding 5% annually might seem attractive. However, if inflation is 3%, the real risk-free rate is only 2%, reflecting the actual increase in purchasing power. Understanding this distinction is fundamental when assessing any investment opportunity. The real risk-free interest rate formula helps to quantify this difference, providing a more accurate measure of the investment’s true profitability.
To further illustrate, consider an investor purchasing a ten-year government bond with a 4% annual yield. If the anticipated inflation rate for the next ten years averages 2%, the real risk-free rate is approximately 2%. This implies that the investor’s purchasing power increases by only 2% annually, not the nominal 4%. This calculation is vital in various financial contexts. It forms the basis for valuing assets, determining the required rate of return on investments, and making informed investment decisions. Ignoring inflation’s effect can lead to inaccurate assessments and suboptimal investment choices. Therefore, accurately calculating and interpreting the real risk-free interest rate formula is paramount for sound financial planning.
The real risk-free rate serves as a benchmark for all other investments. Higher-risk investments demand a higher return than the risk-free rate to compensate for the added risk. This risk premium, added to the real risk-free rate, determines the required return for riskier investments. This principle underpins asset pricing models like the Capital Asset Pricing Model (CAPM), which uses the real risk-free rate as a foundation for calculating expected returns. It is also crucial in capital budgeting, where companies determine the minimum acceptable return on investment projects. Therefore, a thorough understanding of the real risk-free interest rate formula and its implications is essential for effective financial decision-making. The real risk-free rate, a key component of the real risk-free interest rate formula, forms the bedrock of sound financial analysis and strategic planning.
Why is the Real Risk-Free Rate Important?
The real risk-free rate plays a pivotal role in numerous financial decisions. It forms the bedrock for calculating the required return on all investments. This fundamental rate underpins the minimum return an investor expects to compensate for the time value of money and inflation. Without accounting for the real risk-free rate, investment valuations would be significantly skewed, leading to potentially flawed decisions. The real risk-free interest rate formula is crucial in determining this baseline return.
In capital budgeting, the real risk-free rate provides a benchmark against which potential projects are evaluated. Companies use this rate to determine the minimum acceptable return for new investments. A project’s internal rate of return (IRR) must exceed the real risk-free rate to justify the investment. Similarly, in asset pricing models like the Capital Asset Pricing Model (CAPM), the real risk-free rate serves as the base rate for calculating the expected return of an asset. It represents the return investors demand for bearing systematic risk, providing a framework to assess the risk-return trade-off of various assets. Understanding this fundamental rate is therefore vital for efficient portfolio construction and risk management.
Furthermore, bond valuation heavily relies on the real risk-free rate. The real risk-free interest rate formula is incorporated into the discount rate used to determine the present value of future bond cash flows. A higher real risk-free rate leads to lower bond prices, reflecting the increased opportunity cost of investing in fixed-income securities. Accurate estimation of the real risk-free rate is crucial for fair bond pricing and informed investment choices. Its importance extends beyond these applications; it serves as a crucial benchmark for setting interest rates on loans, mortgages, and other forms of credit. Ignoring this rate can lead to inaccurate financial models and inefficient resource allocation. The correct application of the real risk-free interest rate formula ensures sound financial practices across various sectors.
Factors Influencing the Real Risk-Free Rate
Several key factors determine the real risk-free rate. Macroeconomic conditions significantly impact this rate. Strong economic growth often leads to higher inflation expectations. This, in turn, pushes the nominal risk-free rate higher. Conversely, sluggish economic growth might result in lower inflation and a lower real risk-free rate. Monetary policy plays a crucial role. Central banks influence interest rates through tools like the federal funds rate. Their actions directly affect the nominal risk-free rate, subsequently influencing the real risk-free rate. Understanding the real risk-free interest rate formula is crucial for interpreting these effects.
Government policies also exert considerable influence. Fiscal policies, such as government spending and taxation, can impact inflation and economic growth. These policies indirectly affect the real risk-free rate. For example, expansionary fiscal policies might boost inflation, increasing the nominal risk-free rate. Regulations and legal frameworks also matter. Changes in regulations can affect investor confidence and risk perceptions, influencing the real risk-free rate. The real risk-free interest rate formula helps to quantify these influences.
Global economic events further complicate the picture. International trade, geopolitical risks, and global financial crises can all impact the real risk-free rate. For instance, a global recession might lead to lower inflation and reduced investor demand for risk-free assets. This would decrease the nominal risk-free rate and potentially lower the real risk-free rate. Unexpected economic shocks, such as oil price spikes or natural disasters, can also create volatility, making accurate forecasting challenging. The interplay of these factors necessitates careful analysis when using the real risk-free interest rate formula to understand the current economic climate and market conditions. Accurate forecasting of future inflation remains a challenge, despite the availability of sophisticated econometric models. This uncertainty underscores the inherent limitations in calculating the real risk-free rate. The real risk-free interest rate formula should be used with a clear understanding of these limitations.
How to Calculate the Real Risk-Free Rate
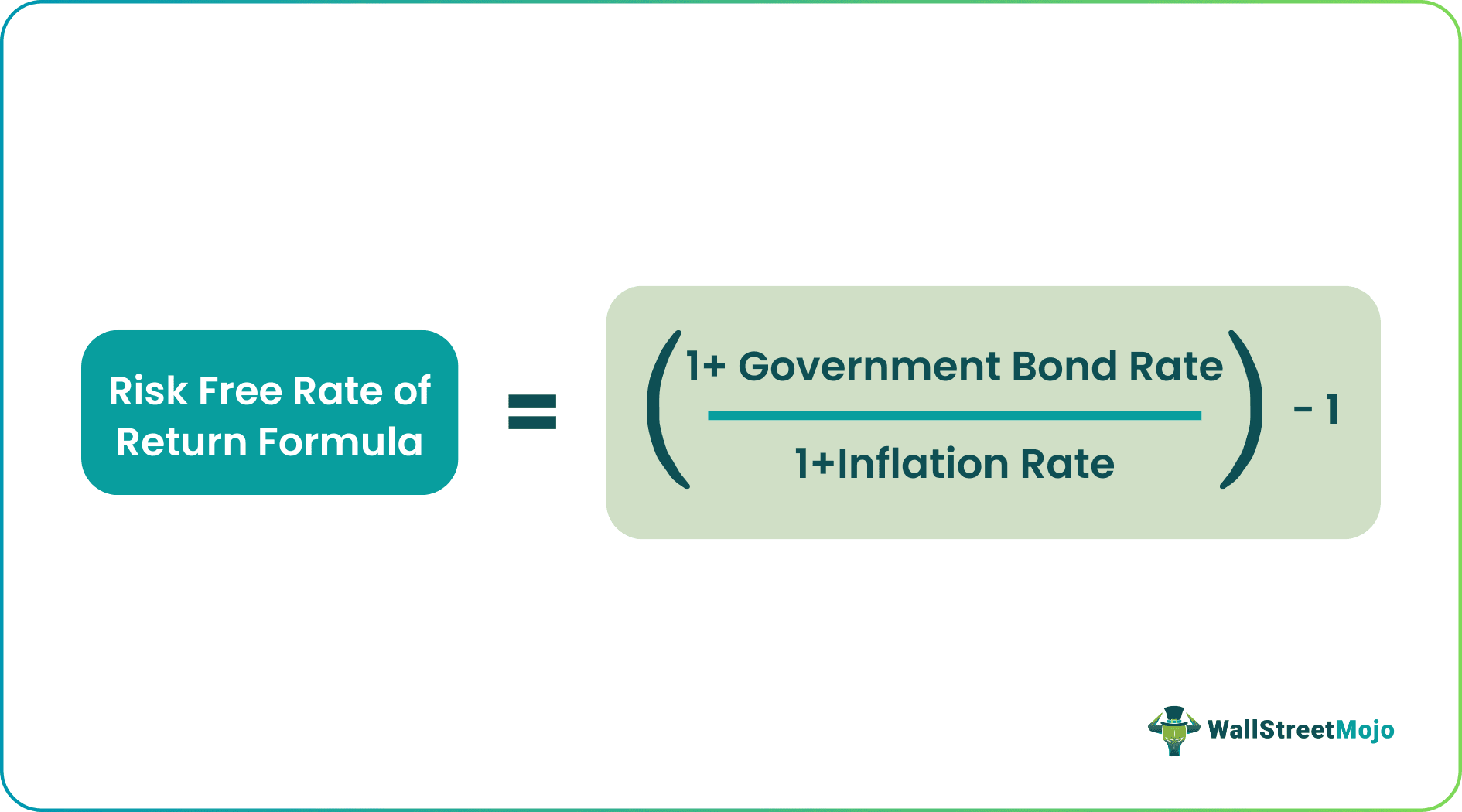
Calculating the real risk-free rate requires a straightforward approach. The core formula, often referred to as the real risk free interest rate formula, is: Real Risk-Free Rate ≈ Nominal Risk-Free Rate – Expected Inflation Rate. The nominal risk-free rate typically represents the yield on a government bond, considered a low-risk investment. The expected inflation rate is a forecast of the future inflation rate. Accurate prediction of future inflation is crucial for a reliable real risk-free rate calculation. Using unreliable inflation forecasts significantly impacts the final result. Data sources such as government statistics offices and central banks provide reliable inflation data for this calculation.
Let’s illustrate this real risk free interest rate formula with examples. Suppose a government bond yields 5% annually (nominal risk-free rate). If economists predict inflation at 2% for the coming year, then the real risk-free rate is approximately 3% (5% – 2%). This indicates that the investment offers a 3% return above inflation. Now, consider a scenario with a nominal risk-free rate of 3% and an expected inflation of 4%. Here, the real risk-free rate becomes approximately -1%. A negative real risk-free rate suggests that the investment’s return fails to outpace inflation. The investor, in this scenario, experiences a loss in purchasing power. The accuracy of the real risk-free rate hinges on the precision of the inflation forecast. Overestimating or underestimating inflation directly influences the final calculation.
Different scenarios demonstrate the versatility of the real risk free interest rate formula. For instance, an environment of low inflation and high nominal yields will produce a higher real risk-free rate, signaling strong investment opportunities. Conversely, periods of high inflation and low nominal yields will likely result in a low or even negative real risk-free rate. This indicates that investors might seek higher-yielding assets to compensate for inflation erosion. Therefore, understanding and correctly applying the real risk free interest rate formula allows for a better understanding of real returns and investment decisions. Remember to always use reliable sources for both the nominal risk-free rate and the expected inflation rate for the most accurate calculation. Using outdated or inaccurate data will inevitably lead to inaccurate results.
Interpreting the Calculated Real Risk-Free Rate
Understanding the calculated real risk-free rate offers valuable insights into economic prospects and investment opportunities. A high real risk-free rate, derived using the real risk free interest rate formula, suggests a strong economy with robust growth and potentially higher inflation expectations. Investors might find fewer attractive fixed-income options, as the return they require is already somewhat high. Conversely, a low real risk-free rate indicates a sluggish economy or low inflation expectations. This environment may favor investments offering higher returns but also higher risk. It’s important to consider the real risk-free rate within the broader economic context. For instance, a low real rate might indicate a period of loose monetary policy aimed at stimulating growth, influencing investor sentiment positively. Conversely, a high real rate could signal a period of tighter monetary policy to curb inflation, leading to a more conservative investor approach. The real risk-free rate is a dynamic indicator, reflecting changing economic conditions and investor behavior.
The real risk-free rate acts as a benchmark. It helps assess the relative attractiveness of different investment options. For example, if the real risk-free rate is 2%, an investment offering a 5% nominal return and 2% expected inflation (resulting in a 3% real return) appears comparatively attractive. However, if inflation expectations rise significantly, the real return on that same investment could fall below the real risk-free rate, making it less appealing. The real risk free interest rate formula is crucial for making these comparisons. It allows investors to make informed decisions and properly assess risks relative to rewards. Businesses also use the real risk-free rate to determine the minimum acceptable return (hurdle rate) for new projects. Projects generating real returns below the real risk-free rate may not be worth the investment risk.
Analyzing the real risk-free rate requires careful consideration of its limitations. The calculation relies heavily on accurate inflation forecasts, which are inherently uncertain. Unexpected economic shocks, such as sudden changes in oil prices or geopolitical events, can significantly impact inflation, rendering the calculated real risk-free rate less precise. Furthermore, the real risk-free rate provides only a snapshot of the economic climate at a specific point in time. It doesn’t account for future uncertainties, which are considerable in long-term investment decisions. Using the real risk free interest rate formula effectively involves acknowledging these limitations and incorporating broader economic and market analyses.
Limitations and Assumptions of the Real Risk-Free Rate Calculation
The calculation of the real risk-free rate, while seemingly straightforward using the real risk free interest rate formula (Nominal Risk-Free Rate – Expected Inflation Rate), relies heavily on accurate forecasts of future inflation. Predicting inflation is inherently challenging. Numerous economic factors influence inflation, and unexpected events can significantly impact its trajectory. The accuracy of the real risk-free rate calculation, therefore, depends on the reliability of inflation forecasts. Overly optimistic or pessimistic inflation predictions directly affect the calculated real rate, potentially leading to inaccurate assessments of investment opportunities. This inherent uncertainty underlines the need for cautious interpretation of the resulting figure. Furthermore, the formula simplifies a complex reality. It assumes a stable and predictable economic environment. However, unforeseen economic shocks, like major geopolitical events or sudden shifts in monetary policy, can invalidate the assumptions underlying the real risk free interest rate formula and render the calculated rate less meaningful. The simplicity of the formula, while useful, means it may not fully capture the nuances of the market.
Another key limitation lies in the choice of the nominal risk-free rate. Different government bonds offer varying yields, reflecting maturity dates and other factors. The selection of a specific bond yield as the nominal risk-free rate introduces subjectivity. The assumption of a constant nominal risk-free rate over the investment horizon may also not hold true, particularly in volatile markets. Shifts in investor sentiment, market expectations, and government actions can all influence the yield on government securities, thus affecting the accuracy of the calculation. Using a historical average of nominal risk free rates might mitigate some of the volatility but may not accurately reflect current market conditions. The real risk free interest rate formula’s accuracy depends on these factors working as assumed; however, the real world doesn’t always align with the assumptions. Therefore, understanding and acknowledging these limitations is critical when using the real risk-free rate in investment decision-making.
The real risk free interest rate formula provides a valuable benchmark, but its limitations must be understood. Investors should treat the calculated rate as an approximation rather than a precise figure. They must consider the potential for error introduced by uncertain inflation forecasts and the simplifying assumptions inherent in the calculation. Using the real risk-free rate in conjunction with other relevant analyses provides a more robust approach to investment decision-making. Furthermore, sensitivity analyses, exploring the impact of varying inflation expectations and nominal risk-free rates, can offer a more comprehensive understanding of the range of possible outcomes. This nuanced perspective helps investors to account for the inherent uncertainty associated with the real risk-free rate. By acknowledging its limitations, investors can leverage its value more effectively.
The Real Risk-Free Rate and Investment Strategy
Understanding the real risk-free rate significantly enhances investment decision-making. Investors can use this rate, often calculated using the real risk free interest rate formula, to evaluate the attractiveness of various investment opportunities. By comparing the expected return of an investment to the real risk-free rate, investors can determine if the potential return adequately compensates for the risk involved. A positive difference suggests the investment offers a sufficient risk premium. This comparison helps investors make informed choices about asset allocation, ensuring their portfolios align with their risk tolerance and return objectives. The real risk-free rate acts as a benchmark, a crucial component for establishing the hurdle rate for new investment projects.
The real risk-free rate influences the minimum acceptable return for any investment. Companies use this rate when evaluating potential projects through discounted cash flow (DCF) analysis. A project’s internal rate of return (IRR) must exceed the real risk-free rate to be considered worthwhile. Similarly, investors use the real risk-free rate to assess the relative attractiveness of bonds. A bond’s yield must be higher than the real risk-free rate to compensate for the risks associated with lending money. Investors can use the real risk free interest rate formula to compute the risk-adjusted return, which helps in comparing bonds with different maturities and risk profiles. This ensures that investment decisions are based on a comprehensive understanding of risk and return.
Moreover, the real risk-free rate plays a pivotal role in portfolio construction. Investors aiming to construct well-diversified portfolios consider the real risk-free rate in their asset allocation strategies. They assess the expected returns of different asset classes (equities, bonds, real estate) relative to this rate. The real risk-free rate helps investors determine the appropriate allocation to each asset class to optimize the risk-return tradeoff. This approach ensures the portfolio is appropriately positioned to achieve the desired level of return while managing overall risk effectively, always considering the real risk free interest rate formula’s implications. Investors can use this rate to create a benchmark for future investment opportunities and make better-informed decisions concerning their investment portfolio. The real risk-free rate provides context for judging risk premiums and helps investors stay disciplined about their investment goals.
The Real Risk-Free Rate in Practice: Real-World Applications
Consider a tech startup evaluating a new product launch. Using the real risk-free interest rate formula, they determine a hurdle rate for the project. This rate, derived from the real risk-free rate plus a risk premium, establishes the minimum acceptable return. If the projected return falls below this hurdle, the project is deemed too risky and may be rejected. The real risk-free interest rate formula provides a crucial benchmark for investment decisions, ensuring projects align with the company’s risk tolerance and return expectations.
In the bond market, investors rely on the real risk-free rate to assess bond yields. A bond offering a nominal yield of 5% might appear attractive. However, if inflation is 3%, the real return is only 2%, using the real risk-free interest rate formula. This calculation helps investors understand the true return after accounting for inflation, enabling informed decisions about bond purchases. Understanding the real risk-free rate is essential for determining the appropriate risk premium to demand for any fixed-income security. This ensures a return that compensates for both the time value of money and the investment’s unique risks.
Large corporations employ the real risk-free rate extensively in capital budgeting. When evaluating major capital expenditures, such as building a new factory or acquiring another company, they use the real risk-free interest rate formula to calculate the discount rate for future cash flows. This ensures the company makes financially sound decisions that consider the time value of money and inflation. A project’s net present value (NPV) is significantly impacted by the discount rate, directly influencing whether or not the project proceeds. The real risk-free rate forms the basis of this critical calculation. A precise calculation using the real risk-free interest rate formula is therefore vital for maximizing corporate value.