Understanding the Concept of the Risk-Free Rate
The risk-free rate of return represents the theoretical return an investor can expect from an investment with zero risk of losing principal. It’s a crucial benchmark in finance, providing a foundation for evaluating the returns of riskier assets. Think of it as the baseline return you could achieve if you absolutely wanted to avoid any chance of losing money. Government bonds, particularly those issued by stable, developed nations, are typically considered risk-free assets because the likelihood of a government defaulting on its debt is extremely low. Understanding the risk-free rate is essential because it helps investors determine the appropriate compensation they should receive for taking on additional risk with other investments. The real risk free interest rate formula plays a crucial role in accurately calculating this benchmark.
This foundational rate serves as a building block for understanding more complex financial concepts. By comparing the return of any investment to the risk-free rate, one can assess the risk premium—the extra return an investor demands for accepting the higher probability of losing some or all of their investment. For instance, a corporate bond might offer a higher yield than a government bond because there’s a greater chance the corporation could default. The difference between the corporate bond’s yield and the risk-free rate represents the additional compensation investors demand for accepting that default risk. The real risk free interest rate formula, while simplified, provides a crucial starting point for this comparison.
The significance of the risk-free rate extends beyond individual investors. Businesses use it extensively in capital budgeting decisions. They incorporate the risk-free rate into discounted cash flow analyses to evaluate the profitability of potential projects. By incorporating the risk-free rate within their calculations, businesses can effectively compare the potential return of an investment to the return they could achieve with a risk-free alternative. A thorough understanding of how the risk-free rate is determined and what factors influence it is crucial for informed decision-making in both investment and business contexts. The real risk free interest rate formula provides a simplified yet foundational tool for this analysis, allowing for a basic comparison between the return of various projects and the return achievable in a risk-free environment. The formula’s simplicity makes it accessible to a wide range of users, from individual investors to large corporations evaluating significant investments.
Factors Influencing the Risk-Free Rate
Several key factors influence the risk-free rate, a crucial component of the real risk free interest rate formula. Inflation expectations significantly impact this rate. High inflation erodes the purchasing power of future returns, thus requiring a higher nominal risk-free rate to compensate investors. For example, if inflation is expected to be 3%, investors will demand a higher return on a risk-free asset to maintain their real purchasing power. Conversely, low inflation allows for lower risk-free rates. The economic growth outlook also plays a crucial role. Strong economic growth often leads to increased demand for capital, driving up interest rates, including the risk-free rate. Conversely, during economic slowdowns or recessions, the risk-free rate tends to fall as demand for borrowing decreases. Central bank policies, particularly interest rate targets, directly influence the risk-free rate. Central banks often adjust interest rates to manage inflation and economic activity. For instance, raising interest rate targets typically increases the risk-free rate, while lowering them reduces it. This influence underscores the dynamic nature of the risk-free rate; it is not a static value but rather fluctuates based on these economic and policy factors. Understanding these influences is crucial for accurately calculating and interpreting the real risk free interest rate formula.
Furthermore, the interplay between these factors creates a complex dynamic impacting the real risk free interest rate formula. For instance, a central bank might raise interest rates to combat high inflation, but if this simultaneously slows economic growth, the effect on the risk-free rate might be less pronounced than expected. Unexpected economic events, such as geopolitical instability or major technological breakthroughs, can also significantly impact the risk-free rate, often leading to short-term volatility. Moreover, global economic conditions influence the risk-free rate in many countries. Changes in global interest rates or economic growth patterns often transmit to domestic markets, impacting the risk-free rate within those countries. This interconnectedness highlights the importance of considering a broader global economic perspective when analyzing and applying the real risk free interest rate formula. Ignoring these complexities can lead to miscalculations and flawed investment decisions.
The impact of these factors on the real risk-free rate, as determined by the real risk free interest rate formula, is not always linear or predictable. For example, the relationship between inflation and the nominal risk-free rate can be complex; during periods of unexpectedly high inflation, the market might overcompensate, resulting in a higher-than-expected increase in the risk-free rate. Similarly, the influence of economic growth can be indirect. A period of strong growth might initially raise the risk-free rate, but if that growth leads to increased inflation, central banks may intervene to curb inflation, potentially negating the initial upward pressure on the risk-free rate. Therefore, accurately predicting the risk-free rate requires a nuanced understanding of these interconnected factors and their potential interactions. The real risk free interest rate formula provides a valuable framework but must be applied cautiously, considering the context and dynamics of the broader economic environment. In essence, while the real risk free interest rate formula is a cornerstone in financial calculations, a comprehensive understanding of these influencing factors is essential for accurate application.
The Nominal vs. Real Risk-Free Rate: Key Differences
Investors often encounter two types of risk-free rates: the nominal risk-free rate and the real risk-free rate. Understanding their distinction is crucial for accurately assessing the true cost of borrowing and the return on investments. The nominal risk-free rate, typically quoted on a bond or other debt instrument, reflects the stated interest rate without adjusting for inflation. Conversely, the real risk-free interest rate formula accounts for the impact of inflation, providing a more accurate measure of the actual return after considering the purchasing power erosion. This difference is critical because inflation erodes the purchasing power of money over time. A high inflation rate can dramatically reduce the true return on an investment, even if the nominal rate appears attractive. For instance, if a bond offers a nominal risk-free interest rate of 5%, but inflation is running at 3%, the real return is only 2%. This 2% represents the actual increase in purchasing power an investor receives.
The distinction between nominal and real risk-free interest rate formula is essential for sound investment decisions. Investors need to understand the real return to properly evaluate the attractiveness of an investment. The real risk-free rate of return provides a clearer picture of the investment’s true value. Without adjusting for inflation, an investor might be misled into believing they are receiving a substantial return, when in reality the return is diminished significantly by the influence of inflation. For instance, a 5% nominal return with a 3% inflation rate equals a 2% real return. This demonstrates that focusing solely on the nominal rate can yield an incorrect assessment of the true worth of the investment. Accurate estimation is crucial when comparing different investment options, assessing the true cost of borrowing, and making well-informed financial decisions. The real risk-free rate serves as a baseline for evaluating other, riskier investments and gauging their additional risk premium.
A crucial aspect to consider is the influence of inflation on investment returns. Inflation acts as a hidden tax on savings and investment returns. If the inflation rate exceeds the return on an investment, the investor’s purchasing power diminishes over time. The real risk-free rate is a critical tool to counter this effect and ensure that investments maintain or improve one’s purchasing power. The nominal risk-free interest rate does not account for this erosion, potentially misleading investors to believe they are earning more than they actually are. By incorporating the real risk-free interest rate formula, one can gain a much clearer picture of the true investment’s worth, enabling informed decision-making. The adjustment for inflation provides a more meaningful reflection of the investment’s performance in relation to the changing value of money. This is essential for investment analysis and portfolio construction.
How to Calculate the Real Risk-Free Rate
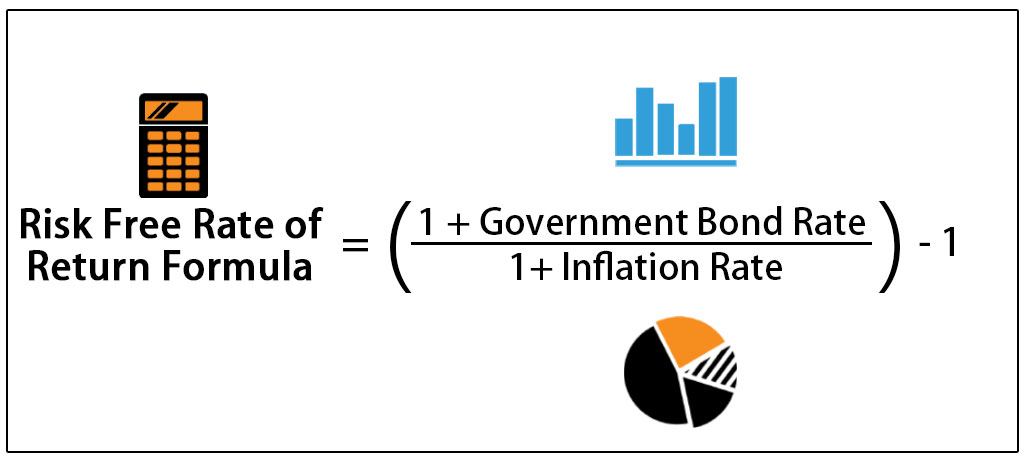
Determining the real risk-free interest rate involves utilizing a fundamental formula, often referred to as the Fisher equation. This equation allows investors to adjust for inflation, providing a clearer picture of the true return on an investment. Understanding this critical component of the real risk-free interest rate formula is essential for informed financial decisions.
The core formula is as follows: (1 + Nominal Risk-Free Rate) = (1 + Real Risk-Free Rate) * (1 + Inflation Rate). This equation can be rearranged to calculate the real risk-free interest rate. A visual representation of this formula can enhance understanding. For instance, a simple diagram illustrating the relationship between nominal, real, and inflation rates would improve comprehension. A step-by-step guide to calculating the real risk-free interest rate is crucial here. Begin by identifying the nominal risk-free rate, often found on government bonds. Next, determine the inflation rate, obtainable from various economic reports. Substituting these values into the formula and solving for the real risk-free rate completes the calculation. For example, if the nominal risk-free rate is 5% and the inflation rate is 2%, the real risk-free interest rate would be approximately 3%. This straightforward example clearly demonstrates the application of the real risk-free interest rate formula.
The Fisher equation is a cornerstone of financial analysis and provides a robust method for calculating the real risk-free interest rate. Understanding its implications is critical for informed decision-making. Through precise calculations, investors can gain invaluable insights into the true cost of borrowing and the return on their investments. Applying the real risk-free interest rate formula consistently across various scenarios provides a practical demonstration of the formula’s versatility. It is important to remember the real risk-free interest rate formula’s underpinning assumptions and limitations, acknowledging potential inaccuracies in real-world applications.
Applying the Formula: Practical Examples
To illustrate the practical application of the real risk-free interest rate formula, consider several scenarios. Let’s begin with a straightforward example. Suppose a government bond yields a nominal rate of 5% and the inflation rate is 2%. Applying the Fisher equation, the real risk-free interest rate would be approximately 3%. This means that, after adjusting for inflation, the investor’s actual return is 3%. Now, let’s introduce a scenario with a higher inflation rate. If the nominal rate remains constant at 5%, but inflation rises to 3%, the real risk-free interest rate would decline to roughly 2%. This clearly demonstrates how inflation directly impacts the real return an investor receives. These examples showcase the versatility of the real risk free interest rate formula and how it helps investors in various contexts to accurately assess the true cost of borrowing.
Let’s examine another example with a nominal rate of 7% and an inflation rate of 4%. In this case, the real risk-free interest rate calculates to approximately 3%. This calculation demonstrates the potential impact on the real return of different levels of inflation on a given nominal interest rate. Variations in nominal interest rates can also affect the real risk free interest rate. For instance, if the nominal rate increases to 9% while inflation remains at 4%, the real risk-free interest rate increases to approximately 5%. These examples highlight the dynamic relationship between nominal rates, inflation rates, and the real risk-free interest rate in investment decisions. The “real risk free interest rate formula” offers a critical tool in assessing the true value of investments, accounting for the eroding impact of inflation.
Further demonstrating the application, consider a situation where a corporate bond yields 8% and the inflation rate is 5%. Using the real risk-free interest rate formula, the real rate comes out to be approximately 3%. This example underscores the significance of the real risk free interest rate formula in evaluating various investment options in the market. Investors and financial institutions can effectively leverage this formula to make informed decisions about investments while accounting for the impact of inflation. By using the real risk free interest rate formula, investors can avoid overestimating returns in inflationary environments and make more accurate comparisons among different investment options.
Limitations of the Real Risk-Free Rate Formula
The Fisher equation, while a useful tool for understanding the real risk-free interest rate formula, possesses certain limitations. It rests on simplifying assumptions that may not perfectly reflect real-world complexities. One primary limitation is the assumption of a constant inflation rate. In reality, inflation fluctuates over time, and projecting a constant inflation rate for extended periods can lead to inaccuracies in the calculation of the real risk-free interest rate formula. Furthermore, the Fisher equation treats inflation as a uniform factor affecting all investments. However, different assets and market segments may experience varying degrees of inflation risk. In practice, the real risk-free interest rate formula and its application are subject to adjustments and modifications to compensate for these non-uniformities. Another crucial factor often excluded from simple calculations is the effect of liquidity and market conditions on bond prices. Market volatility and fluctuations in investor confidence can impact the perceived risk of government bonds, affecting their yields and the resultant real risk-free interest rate formula. The real risk-free interest rate formula only considers nominal yields and inflation expectations. It does not explicitly account for potential risks like default risk, where the borrower might not repay the loan. Furthermore, the formula does not incorporate potential changes in the monetary policy environment. While helpful, the real risk-free interest rate formula should be considered a theoretical starting point and not a precise predictor of actual real-world borrowing costs. Investors and analysts should always use caution when interpreting the outcomes and should incorporate other relevant factors into their assessment for a more robust understanding.
The real risk-free interest rate formula, derived from the Fisher equation, offers a valuable theoretical construct for estimating the true cost of borrowing. Nevertheless, its application should be coupled with an awareness of its inherent limitations. It’s essential to acknowledge that the calculated value represents a simplified model, and the real-world rate may differ due to unquantifiable factors. The formula’s results should not be used in isolation but should be part of a more comprehensive assessment that accounts for additional risk factors such as default, liquidity, and market risks. Investors should be aware that the real risk-free interest rate formula is a theoretical concept that should not be considered a precise measure of true costs in specific scenarios. The calculation of the real risk-free interest rate formula requires careful consideration of the limitations and assumptions associated with the Fisher equation. Further, incorporating more sophisticated models and adjustments is needed for a robust and comprehensive approach to investment analysis.
The limitations of the real risk-free interest rate formula highlight the importance of considering various risk factors beyond the fundamental ones captured in the equation. A thorough risk analysis incorporating market volatility, economic fluctuations, default risk, and liquidity risk is crucial to arrive at a more realistic estimation of borrowing costs. Additional consideration should be given to macroeconomic conditions, investor sentiment, and specific market dynamics that could influence borrowing costs beyond the straightforward application of the real risk-free interest rate formula.
Using the Real Risk-Free Rate in Investment Decisions
Investors and businesses can leverage the calculated real risk-free interest rate formula in their decision-making processes. Understanding the real return on an investment, adjusted for inflation, is crucial for evaluating the attractiveness of various assets. The real risk-free rate serves as a benchmark for assessing the return of other assets, such as stocks or bonds, by comparing their returns to the real risk-free rate. This comparison helps determine if the potential return of an asset compensates for the additional risk involved. Additionally, the real risk-free rate can be employed as a key input in discounted cash flow (DCF) analysis, specifically in setting discount rates for net present value (NPV) calculations. Accurate NPV estimations, which are integral to investment appraisal, rely heavily on the precise calculation of the discount rate. Consequently, the real risk-free rate is a critical component in project evaluation and capital budgeting decisions. Recognizing and quantifying the real return provides essential insights into the financial viability of proposed projects.
Furthermore, the real risk-free interest rate formula is fundamental to proper risk management. When assessing potential projects, determining the real risk-free rate helps businesses evaluate the real return required to offset the inherent risks associated with an investment. This evaluation allows informed choices, focusing on projects with returns that exceed their associated risks. Critically, the use of the real risk-free rate should be coupled with an assessment of risk premiums. Risk premiums, which account for different risk types, are crucial for accurate investment decisions. A comprehensive approach to investment analysis, integrating both the real risk-free rate and risk premiums, provides a more realistic valuation of an asset’s true cost and return. The precise calculation of risk premiums further ensures a realistic evaluation of future returns.
In summary, the real risk-free rate serves as a vital component in investment decisions, enabling a comparison between the expected returns of various assets and their associated risks. It facilitates accurate NPV calculations, plays a pivotal role in capital budgeting, and when paired with risk premiums, provides a more thorough investment analysis. Consequently, integrating the real risk-free rate formula into investment strategies contributes to more informed and financially sound decisions.
Beyond the Formula: Incorporating Other Risk Factors
The real risk-free rate, as calculated using the real risk-free interest rate formula, serves as a crucial foundational element in investment analysis, providing a baseline for understanding the potential return of an investment before considering any risk. However, it’s vital to remember that this calculation represents a simplified view of reality. While the formula offers a valuable starting point, it’s essential to incorporate additional risk factors to gain a more comprehensive understanding of an investment’s true potential return and associated risks. Ignoring these other factors can lead to inaccurate assessments and potentially poor investment decisions. The real risk-free interest rate formula, while useful, is only one piece of a much larger puzzle.
Several critical risk factors must be considered alongside the real risk-free rate. Default risk, the probability that the borrower will fail to repay the debt, is a significant concern for investors. Government bonds typically carry minimal default risk, but corporate bonds and other debt instruments expose investors to varying degrees of this risk. Liquidity risk, the risk that an asset cannot be quickly bought or sold without impacting its price, is another essential factor. Highly liquid assets like government bonds can be easily traded, minimizing liquidity risk, while less liquid assets may require accepting a lower price for a quick sale. Market risk, encompassing broader economic and market fluctuations, represents another layer of uncertainty. Changes in interest rates, economic downturns, or shifts in investor sentiment can significantly impact asset values, regardless of the underlying real risk-free interest rate.
Sophisticated models used by financial professionals often build upon the fundamental concepts underlying the real risk-free interest rate formula. These models incorporate a wider array of risk factors, allowing for a more nuanced assessment of potential returns and risks. They may employ statistical techniques to estimate the probabilities of various outcomes and incorporate the impact of complex interactions between different risk factors. Ultimately, understanding the real risk-free rate is crucial, but it’s only the first step in a thorough investment analysis. A comprehensive evaluation requires acknowledging and quantifying the additional risks inherent in any investment opportunity, going beyond the simplified view provided by the real risk-free interest rate formula alone. A complete picture requires a more holistic approach that integrates multiple risk factors and sophisticated modeling techniques.