What is Brownian Motion and Why is it Important?
Brownian motion, a fundamental concept in stochastic processes, describes the random movement of particles suspended in a fluid. This phenomenon was first observed in 1827 by Scottish botanist Robert Brown and has since been extensively studied in various fields, including physics, biology, and finance. Brownian motion is essential in understanding and modeling random fluctuations and uncertainty, which are inherent in many natural and financial systems. The concept has far-reaching implications, from understanding the behavior of molecules in a gas to modeling stock prices in financial markets. In fact, the quadratic variation of Brownian motion plays a crucial role in analyzing stochastic processes, allowing researchers to quantify and manage uncertainty in complex systems. By grasping the principles of Brownian motion, scientists and financial analysts can better comprehend and predict the behavior of systems that are inherently unpredictable.
Understanding the Quadratic Variation of Brownian Motion
Quadratic variation is a fundamental concept in stochastic processes that plays a crucial role in analyzing Brownian motion. It is a mathematical tool used to quantify the cumulative effect of small, random fluctuations in a system over time. In the context of Brownian motion, quadratic variation measures the squared changes in the position of a particle suspended in a fluid, providing valuable insights into the underlying dynamics of the system. The quadratic variation of Brownian motion is a key component in modeling and understanding stochastic processes, as it allows researchers to capture the intricate patterns and behaviors of complex systems. By grasping the principles of quadratic variation, scientists and analysts can better comprehend the intricacies of Brownian motion and its applications in various fields, including finance, biology, and physics.
How to Calculate Quadratic Variation of Brownian Motion
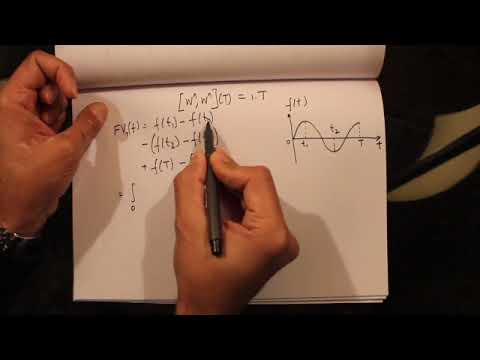
To calculate the quadratic variation of Brownian motion, it is essential to understand the mathematical formulas and concepts involved. The quadratic variation of a Brownian motion process, denoted by [W(t)], can be calculated using the following formula: [V(t) = lim(n→∞) ∑[W(ti)-W(ti-1)]^2], where [V(t)] is the quadratic variation, [W(ti)] is the Brownian motion process at time [ti], and [n] is the number of partitions. This formula provides a discrete approximation of the quadratic variation, which can be used to analyze the stochastic process. In practice, the calculation of quadratic variation involves dividing the time interval into smaller partitions and summing the squared increments of the Brownian motion process. The resulting value represents the cumulative effect of the random fluctuations in the system over time. By applying this formula, researchers and analysts can gain valuable insights into the behavior of Brownian motion and its applications in various fields, including finance, biology, and physics. The quadratic variation of Brownian motion is a powerful tool for understanding and modeling complex systems, and its calculation is a crucial step in unlocking its potential.
The Role of Quadratic Variation in Financial Modeling
In financial modeling, the quadratic variation of Brownian motion plays a crucial role in understanding and managing uncertainty in financial markets. By analyzing the quadratic variation of Brownian motion, financial analysts and researchers can gain valuable insights into the behavior of asset prices, risk management, and portfolio optimization. The quadratic variation of Brownian motion is used to model the volatility of asset prices, which is essential for pricing options and other derivatives. In risk management, the quadratic variation of Brownian motion helps to quantify the potential losses and gains of a portfolio, enabling investors to make informed decisions. Furthermore, the quadratic variation of Brownian motion is used in portfolio optimization to determine the optimal allocation of assets, maximizing returns while minimizing risk. The application of quadratic variation of Brownian motion in financial modeling has revolutionized the field, providing a powerful tool for understanding and managing uncertainty in financial markets. By incorporating the quadratic variation of Brownian motion into financial models, researchers and analysts can develop more accurate and reliable predictions, ultimately leading to better investment decisions.
Real-World Applications of Quadratic Variation of Brownian Motion
The quadratic variation of Brownian motion has far-reaching implications in various fields, including biology, physics, and engineering. In biology, the quadratic variation of Brownian motion is used to model the movement of particles in complex systems, such as the diffusion of molecules in cells. This helps researchers understand the underlying mechanisms of biological processes and develop new treatments for diseases. In physics, the quadratic variation of Brownian motion is used to study the behavior of particles in random environments, such as the motion of atoms in a gas. This has led to a deeper understanding of the fundamental laws of physics and the development of new materials and technologies. In engineering, the quadratic variation of Brownian motion is used to model and analyze complex systems, such as communication networks and financial markets. This helps engineers design more efficient and reliable systems, and develop new technologies to manage uncertainty and risk. The quadratic variation of Brownian motion has also been used to model and analyze other complex systems, such as traffic flow, population dynamics, and climate models. The applications of quadratic variation of Brownian motion are vast and diverse, and continue to grow as researchers and scientists explore new ways to apply this powerful tool.
Challenges and Limitations of Quadratic Variation of Brownian Motion
While the quadratic variation of Brownian motion is a powerful tool for analyzing stochastic processes, it is not without its challenges and limitations. One of the main assumptions of the quadratic variation of Brownian motion is that the underlying process is a continuous-time stochastic process, which may not always be the case in real-world applications. Additionally, the quadratic variation of Brownian motion relies on the concept of infinitesimal increments, which can be difficult to interpret and apply in practice. Furthermore, the quadratic variation of Brownian motion is sensitive to the choice of time interval and sampling frequency, which can affect the accuracy of the results. Another limitation of the quadratic variation of Brownian motion is that it is based on a Gaussian distribution, which may not be suitable for modeling non-normal or heavy-tailed distributions. Moreover, the quadratic variation of Brownian motion can be computationally intensive, especially for large datasets. Despite these challenges and limitations, the quadratic variation of Brownian motion remains a widely used and powerful tool for analyzing stochastic processes, and ongoing research is addressing these limitations to improve its applicability and accuracy.
Advancements and Future Directions in Quadratic Variation Research
Research in quadratic variation of Brownian motion is an active and rapidly evolving field, with new mathematical techniques and applications emerging continuously. One of the recent advancements is the development of new estimation methods for quadratic variation, such as the realized quadratic variation and the pre-averaging method. These methods have improved the accuracy and efficiency of quadratic variation estimation, enabling researchers to analyze complex systems with greater precision. Another area of research is the application of quadratic variation to emerging fields such as machine learning and artificial intelligence. For example, quadratic variation has been used to develop new algorithms for anomaly detection and risk analysis in complex systems. Furthermore, researchers are exploring the use of quadratic variation in modeling and analyzing complex systems in fields such as climate science, epidemiology, and social network analysis. The future directions of quadratic variation research are exciting and promising, with potential applications in areas such as quantum finance, high-frequency trading, and cybersecurity. As research in quadratic variation of Brownian motion continues to advance, it is likely to unlock new insights and opportunities in a wide range of fields, from physics and biology to finance and engineering.
Conclusion: Unlocking the Power of Quadratic Variation in Stochastic Processes
In conclusion, the quadratic variation of Brownian motion is a powerful tool for analyzing stochastic processes, with far-reaching applications in fields such as finance, biology, physics, and engineering. By understanding the quadratic variation of Brownian motion, researchers and practitioners can better model and analyze complex systems, manage uncertainty, and make informed decisions. The importance of quadratic variation of Brownian motion lies in its ability to provide insights into the underlying dynamics of stochastic processes, enabling the development of more accurate and effective models. As research in quadratic variation of Brownian motion continues to advance, it is likely to unlock new insights and opportunities in a wide range of fields, from understanding the behavior of complex systems to developing new mathematical techniques and applications. The significance of continued research in this area cannot be overstated, as it has the potential to revolutionize our understanding of stochastic processes and drive innovation in various fields. By embracing the power of quadratic variation of Brownian motion, we can unlock new possibilities and opportunities, and gain a deeper understanding of the complex systems that shape our world.