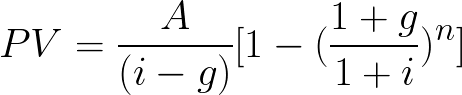Pv of Growing Annuity Formula

Grasping the Concept of an Increasing Annuity

An increasing annuity, also known as a growing annuity, represents a series of payments that increase at a constant rate over a specified period. Unlike a standard annuity where payments remain fixed, an increasing annuity reflects a predictable growth pattern. This growth factor makes it a valuable tool for modeling financial scenarios where income or expenses are expected to rise over time.

Consider these real-world examples to illustrate the concept. Lease agreements often incorporate annual rent escalations, reflecting increases in property value or operating costs. Similarly, some pension plans offer cost-of-living adjustments (COLAs), ensuring that retirees’ income keeps pace with inflation. Another example is projected salary increases. The pv of growing annuity formula helps to determine the present value of these future income streams, allowing for informed financial planning. Understanding the nature of these escalating payments is crucial before delving into the pv of growing annuity formula.

The primary difference between an increasing annuity and a regular annuity lies in the payment structure. A regular annuity involves consistent, unchanging payments throughout its term. In contrast, an increasing annuity features payments that grow at a predetermined rate. Recognizing this distinction is essential when choosing the appropriate valuation method. The pv of growing annuity formula is specifically designed to handle the complexities introduced by the growing payment stream. Therefore, for situations involving escalating payments, the pv of growing annuity formula offers a more accurate and realistic assessment compared to the standard annuity calculations. Before applying the pv of growing annuity formula, confirm that the scenario involves payments that increase at a steady rate. Ignoring this aspect and misapplying formulas will lead to incorrect financial analysis. The pv of growing annuity formula is a powerful tool when correctly applied.

What is the Formula for Calculating Present Value of a Growing Annuity?

The present value (PV) of a growing annuity represents the current worth of a series of future payments that increase at a constant rate. Understanding the pv of growing annuity formula is crucial for various financial analyses, from investment valuation to retirement planning. The formula itself incorporates several key variables, each playing a distinct role in determining the final present value. Accurately applying this formula enables informed decision-making regarding investments and financial strategies. It is the cornerstone for properly calculating the value of escalating income streams.

The core pv of growing annuity formula is expressed as: PV = C / (r – g) * [1 – (1 + g)^n / (1 + r)^n], where each element is defined as follows:

• PV: Represents the Present Value of the growing annuity. This is the value you are trying to determine – the current worth of all future payments. For example, if you are evaluating an investment, the PV tells you what that future stream of income is worth today.
• C: Stands for the initial payment or cash flow in the series. This is the amount of the first payment you will receive. For instance, if your growing lease payment starts at $1,000 per month, then C = $1,000.
• r: Denotes the discount rate, which reflects the rate of return that could be earned on an alternative investment with similar risk. A higher discount rate implies a lower present value. For example, if you could earn 8% on another investment with similar risk, then r = 0.08.
• g: Represents the growth rate of the annuity payments. This is the percentage by which each subsequent payment increases. For example, if your payments increase by 3% each year, then g = 0.03.
• n: Signifies the number of periods over which the payments will be made. This is the total number of payments in the annuity. For instance, if you will receive payments for 10 years, then n = 10.

Understanding and correctly identifying each of these variables is essential for accurately calculating the pv of growing annuity formula. Failing to properly define any variable can lead to significant errors in the present value calculation, potentially impacting the quality of financial decisions made based on it.

A Step-by-Step Guide: How to Calculate the Present Value of an Escalating Annuity

This section offers a detailed, step-by-step guide on how to effectively use the pv of growing annuity formula. A numerical example clarifies each calculation step. The goal is to promote understanding and prevent common errors. Calculating the present value (PV) of a growing annuity can seem complex. However, breaking it down into manageable steps simplifies the process. Let’s consider an example: Suppose you are evaluating an investment that will pay you $1,000 next year. This payment will increase by 3% each year for the next 5 years. Your required rate of return, or discount rate, is 8%. What is the pv of growing annuity formula for this investment?

Step 1: Identify the Variables. First, identify all variables. C (Cash flow next year) = $1,000. r (Discount rate) = 8% or 0.08. g (Growth rate) = 3% or 0.03. n (Number of periods) = 5 years. Step 2: Apply the Formula. The pv of growing annuity formula is: PV = C * [1 – ((1 + g) / (1 + r))^n] / (r – g). Substitute the values: PV = $1,000 * [1 – ((1 + 0.03) / (1 + 0.08))^5] / (0.08 – 0.03). Step 3: Simplify the Calculation. Begin by simplifying within the brackets. (1 + 0.03) = 1.03. (1 + 0.08) = 1.08. (1.03 / 1.08) = 0.9537. Then, raise this to the power of n (which is 5): (0.9537)^5 = 0.7829. Subtract this result from 1: 1 – 0.7829 = 0.2171. Now, address the denominator: (0.08 – 0.03) = 0.05. Step 4: Final Calculation. Divide the result from Step 3 by the denominator: 0.2171 / 0.05 = 4.342. Finally, multiply this by the initial cash flow (C): $1,000 * 4.342 = $4,342. Therefore, the present value of this growing annuity is $4,342.

Avoiding Common Mistakes. A common mistake is incorrectly inputting the variables. Ensure the growth rate and discount rate are in decimal form. Also, double-check the number of periods. Another error involves misunderstanding the order of operations. Follow the formula precisely to avoid incorrect results. Using a financial calculator or spreadsheet software can also help reduce calculation errors when determining the pv of growing annuity formula. Always review your inputs and results to ensure accuracy. This step-by-step approach, combined with careful attention to detail, will enable you to confidently calculate the present value of a growing annuity.

When to Employ the Present Value of a Growth Annuity Calculation

The pv of growing annuity formula is a versatile tool applicable in various financial scenarios. Understanding when to use it can significantly improve decision-making. One common application is in investment analysis. When evaluating an investment that is expected to generate increasing cash flows over time, the pv of growing annuity formula helps determine its present value. This allows investors to compare different investment opportunities and select the most profitable ones. For example, consider a rental property where the rental income is expected to increase annually. Calculating the present value of these growing rental payments provides a more accurate assessment of the property’s worth than simply using the current rental income.

Real estate analysis is another area where this formula proves valuable. It assists in determining the fair price of a property with projected increases in rental income. Similarly, it can be used to evaluate lease agreements with escalating payments. By calculating the present value of these future payments, businesses can make informed decisions about leasing versus purchasing assets. Retirement planning also benefits from the pv of growing annuity formula. Individuals planning for retirement may receive pensions or social security benefits that are adjusted for inflation or cost-of-living increases. Using this formula, one can estimate the present value of these future income streams and assess whether they will be sufficient to meet their retirement needs. The pv of growing annuity formula offers a more realistic view of the value of future income compared to a standard annuity calculation, especially in an inflationary environment.>

Moreover, the advantages of using the pv of growing annuity formula extend beyond simple valuation. It provides a more nuanced understanding of the impact of growth rates and discount rates on present value. This understanding is crucial for making sound financial decisions. For instance, understanding the impact of different growth rates on the present value of an investment can help investors choose investments with higher growth potential. In corporate finance, the formula can be used to evaluate projects with increasing cash flows, aiding in capital budgeting decisions. By incorporating growth expectations, businesses can make more accurate assessments of project profitability and make informed investment choices. In essence, the pv of growing annuity formula empowers individuals and organizations to make well-informed financial decisions by accurately valuing future income streams that are expected to grow over time.

The Relationship Between Growth Rate and Discount Rate: A Crucial Consideration

The relationship between the growth rate (g) and the discount rate (r) is paramount when calculating the present value of a growing annuity. These two rates significantly impact the calculated present value, and understanding their interplay is essential for accurate financial analysis. The formula used to determine the pv of growing annuity formula relies on this relationship.

When the growth rate (g) is less than the discount rate (r), the present value of the increasing annuity can be calculated using the standard formula. This scenario is the most common, where the return required (discount rate) is higher than the rate at which the annuity payments are increasing. If g is smaller than r, the pv of growing annuity formula provides a finite and realistic present value. However, if g is greater than r, the formula yields a negative present value, which is economically meaningless. This implies that the annuity payments are growing at a faster rate than they are being discounted, suggesting an unsustainable scenario in most practical situations. In such instances, the standard present value formula is not applicable.

The special case occurs when the growth rate (g) equals the discount rate (r). In this situation, the standard pv of growing annuity formula is undefined because it would involve division by zero. A different approach is required to calculate the present value when g = r. In this scenario, the present value is simply the sum of all the payments, each discounted back to the present at the same rate at which they are growing. This can be calculated as PV = n * C / (1+r), where n is the number of periods, C is the initial payment, and r is the discount rate (which is equal to the growth rate in this case). Ignoring the relationship between ‘g’ and ‘r’ can lead to substantial errors in financial planning and investment analysis. A clear understanding of these concepts is crucial for the proper application of the pv of growing annuity formula. Therefore, always verify this relationship before applying the pv of growing annuity formula.

Practical Applications: Real-World Examples of Present Value of a Growing Annuity

The pv of growing annuity formula proves invaluable in numerous financial scenarios. Consider a commercial real estate investment. An investor is evaluating a property where lease payments are structured to increase by 3% annually. The current annual lease income is $100,000, and the investor anticipates holding the property for 10 years. To determine a fair purchase price, the investor needs to calculate the present value of this stream of escalating lease payments. Assuming a discount rate of 8% reflecting the investor’s required rate of return, the pv of growing annuity formula can accurately determine the present value.

Using the pv of growing annuity formula, the calculation reveals the present value of the lease income stream. In this instance: PV = C * [1 – ((1 + g) / (1 + r))^n] / (r – g), where C = $100,000, g = 3%, r = 8%, and n = 10 years. Plugging these values into the formula yields a present value of approximately $824,242. This figure represents the maximum price the investor should be willing to pay for the property, solely based on the projected lease income. If the asking price exceeds this present value, the investment might not meet the investor’s required rate of return, making it a less attractive opportunity. This analysis showcases the power of the pv of growing annuity formula in evaluating investment opportunities with increasing cash flows.

Another application of the pv of growing annuity formula is in retirement planning. Imagine an individual expecting to receive annual pension payments that increase with inflation. These payments start at $40,000 per year and are projected to grow at a rate of 2% annually for the next 25 years. To assess the present value of these future pension benefits, a financial planner can employ the pv of growing annuity formula. Assuming a discount rate of 6%, representing the expected return on investments, the formula helps determine the lump sum equivalent of the future pension stream. In this case: PV = C * [1 – ((1 + g) / (1 + r))^n] / (r – g), where C = $40,000, g = 2%, r = 6%, and n = 25 years. The result provides an understanding of the current value of their future retirement income. This example illustrates how this formula aids in understanding the true value of financial instruments that provide an increasing income stream over time. It also allows for better informed decisions about savings and investment strategies.

Navigating Common Pitfalls When Calculating Increasing Annuities

Calculating the present value of a growing annuity can be complex, and several common errors can lead to inaccurate results. One frequent mistake is incorrect input of variables into the pv of growing annuity formula. Ensure that the values for the initial payment (C), discount rate (r), growth rate (g), and number of periods (n) are all accurate and consistent with the time frame being analyzed. For instance, if payments are made monthly, the discount and growth rates should also be expressed monthly.

Another pitfall is using the wrong formula altogether. It’s crucial to distinguish between the pv of growing annuity formula and the formula for a regular annuity or a perpetuity. The growing annuity formula specifically accounts for the consistent growth of payments over time. Applying an incorrect formula will inevitably lead to an inaccurate present value calculation. A misunderstanding of the time value of money is another significant source of error. Remember that money received in the future is worth less than money received today, and the discount rate reflects this difference. Failing to adequately account for the time value of money will result in an overestimation of the present value.

Furthermore, pay close attention to the relationship between the growth rate (g) and the discount rate (r). The pv of growing annuity formula is only valid when r > g. If the growth rate equals or exceeds the discount rate, the formula produces nonsensical results, indicating that the annuity’s value grows infinitely. In such cases, alternative valuation methods may be necessary. To avoid these errors, double-check all inputs, ensure the correct formula is used, and carefully consider the relationship between the growth rate and the discount rate when calculating the pv of growing annuity formula. By understanding and addressing these potential pitfalls, one can confidently and accurately determine the present value of an increasing annuity.

Simplifying Complex Financial Decisions with Growing Annuity Analysis

Understanding and applying the present value of a growing annuity formula offers significant advantages when navigating intricate financial landscapes. This powerful tool allows for a more accurate assessment of investments that feature increasing cash flows, leading to better-informed decisions. The pv of growing annuity formula enables individuals and organizations to quantify the true value of opportunities that might otherwise be misjudged using simpler valuation methods. This is particularly relevant in scenarios involving long-term projections, where the impact of growth rates and discount rates can significantly alter the perceived value. Financial planning, investment analysis, and real estate valuation are just a few areas where the formula proves invaluable.

The ability to accurately calculate the present value of a growing annuity empowers users to make strategic decisions. For instance, when evaluating different investment options, the pv of growing annuity formula helps compare opportunities with varying growth rates and initial investment costs on a level playing field. This leads to the selection of options that provide the highest risk-adjusted returns. In retirement planning, understanding the present value of future income streams that increase over time, such as cost-of-living adjusted pensions, is crucial for ensuring financial security. By accounting for the time value of money and the expected growth rate, individuals can more effectively plan for their future needs and adjust their savings strategies accordingly. Furthermore, by using the pv of growing annuity formula, real estate investors can determine the fair price to pay for properties with escalating rental income.

In conclusion, mastering the pv of growing annuity formula is an invaluable asset in the world of finance. It provides a framework for understanding the true worth of investments and financial obligations that exhibit growth over time. By carefully considering the interplay between growth rates, discount rates, and the time value of money, users can make sound financial decisions, optimize their investment portfolios, and plan for a more secure financial future. Its application extends across diverse sectors, from personal finance to corporate investment, highlighting its versatility and importance in today’s complex economic environment. By embracing this knowledge, individuals and organizations alike can unlock new opportunities and mitigate risks, leading to improved financial outcomes.