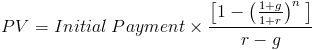Understanding Annuities and Their Growth
An annuity represents a series of equal payments made at fixed intervals. A growing annuity, however, features payments that increase at a consistent rate over time. This growth factor significantly impacts the overall value of the annuity. Understanding the present value (PV) of a growing annuity is crucial. The PV of a growing annuity formula calculates the current worth of this future stream of increasing payments. This is essential for making informed financial decisions, especially when dealing with investments or long-term financial planning. The pv of a growing annuity formula allows for a precise valuation of these financial instruments. Investors and financial planners utilize the pv of a growing annuity formula to make sound investment choices and retirement strategies. Understanding this formula empowers individuals to make more accurate assessments of financial opportunities involving growing payments.
The concept of present value is fundamental. It reflects the current value of a future sum of money, considering the time value of money. Money received today is worth more than the same amount received in the future due to its potential earning capacity. The pv of a growing annuity formula directly addresses this concept by discounting future growing payments back to their present-day equivalent. This makes comparing investments with different payment structures easier and more accurate. The formula helps determine whether the expected returns justify the present investment. Applying the pv of a growing annuity formula properly can significantly improve financial planning and decision-making processes.
Accurate calculation of the pv of a growing annuity is paramount for various financial applications. The formula incorporates factors such as the rate of growth, the discount rate (interest rate), and the number of payment periods. The pv of a growing annuity formula provides a clear and concise method for assessing the current worth of future income streams. This formula helps in comparing different investment options and making informed financial choices. By understanding and correctly applying the pv of a growing annuity formula, individuals can make well-informed decisions that align with their financial goals.
Why is the Present Value of a Growing Annuity Important?
Understanding the pv of a growing annuity formula offers significant advantages in various financial scenarios. Investors frequently use this calculation to determine the fair value of investments providing growing dividend payments. The pv of a growing annuity formula helps assess the present worth of these future cash flows, aiding informed investment decisions. This is crucial for making comparisons between different investment options and optimizing portfolio returns. Accurate valuation using the pv of a growing annuity formula directly impacts investment success.
Businesses also rely heavily on the pv of a growing annuity formula for valuation purposes. Companies with steadily increasing revenue streams can use this formula to estimate their current market value. This is particularly important for startups or businesses planning mergers and acquisitions. The formula helps to determine a fair price based on projected future earnings, making it a critical tool in financial modeling and corporate finance. Accurate valuation using the pv of a growing annuity formula is essential for successful transactions.
Retirement planning further benefits from the application of the pv of a growing annuity formula. Individuals can use this formula to determine how much they need to save today to ensure a comfortable retirement with a steadily increasing income stream. Factors like inflation and increasing living expenses are considered when using the formula. This ensures that the retirement plan remains sustainable and adequately funds future needs. Using the pv of a growing annuity formula for retirement planning promotes financial security and peace of mind.
Breaking Down the pv of a growing annuity formula: A Step-by-Step Explanation
The pv of a growing annuity formula calculates the current worth of a series of future payments that increase at a constant rate. The formula itself is: PV = PMT / (r – g) * [1 – (1 + g / 1 + r)^n]. Understanding this pv of a growing annuity formula requires defining each variable. PV represents the present value, the total current worth of all future payments. PMT stands for the payment amount of the first annuity payment. The variable ‘r’ signifies the discount rate, representing the return an investor expects on their investment. ‘g’ denotes the growth rate of the annuity payments, meaning the percentage by which each subsequent payment increases. Finally, ‘n’ represents the number of periods the payments will be received.
This pv of a growing annuity formula is crucial for financial planning. The discount rate (r) reflects the opportunity cost of the investment; a higher discount rate reduces the present value. The growth rate (g) directly impacts the present value. A higher growth rate increases the present value because future payments are worth more. The number of periods (n) also significantly affects the present value; a longer time horizon increases the present value. Accurate calculation using the pv of a growing annuity formula demands careful attention to each of these inputs. Misinterpreting any one could lead to inaccurate results. The formula relies on consistent application; changes in any variable directly impact the outcome, underlining the importance of using accurate data. The pv of a growing annuity formula is exceptionally useful for valuing assets with consistent growth, offering invaluable insight into long-term financial decisions.
Mastering the pv of a growing annuity formula involves understanding its limitations. The formula assumes a constant growth rate and a constant discount rate. Real-world scenarios rarely maintain perfect consistency. Furthermore, the formula doesn’t account for taxes or fees, factors that can substantially reduce the actual present value. Despite these limitations, the pv of a growing annuity formula provides a strong foundation for valuing growing income streams. By understanding its components and potential shortcomings, investors and financial planners can make more informed decisions using this practical tool. The formula’s core value lies in its ability to model future cash flows, offering a structured approach to assessing investment opportunities and their long-term worth. Understanding the pv of a growing annuity formula is essential for financial literacy and strategic decision-making.
How to Calculate the Present Value of a Growing Annuity: A Step-by-Step Example
Let’s illustrate the pv of a growing annuity formula with a practical example. Suppose an investor anticipates receiving annual payments of $1,000 from an investment. These payments increase by 3% each year. The investor’s discount rate (the rate of return they could earn on alternative investments) is 8%. The payments will continue for 10 years. To determine the present value of this growing annuity, we will use the formula: PV = PMT / (r – g) * [1 – (1 + g / 1 + r)^n]. Here, PMT = $1,000 (annual payment), r = 0.08 (discount rate), g = 0.03 (growth rate), and n = 10 (number of years).
First, calculate the term (1 + g / 1 + r)^n: (1 + 0.03 / 1 + 0.08)^10 ≈ 0.737. Next, substitute the values into the pv of a growing annuity formula: PV = $1,000 / (0.08 – 0.03) * [1 – 0.737]. This simplifies to PV = $1,000 / 0.05 * [0.263]. Therefore, the present value of this growing annuity is approximately $5,260. This calculation demonstrates how to effectively use the pv of a growing annuity formula to determine the current worth of future increasing cash flows. The formula accurately reflects the time value of money, considering both the size and timing of the growing payments. Remember, accurate input of variables is crucial for an accurate result using the pv of a growing annuity formula. Even small errors in the growth rate or discount rate can significantly alter the final present value.
Understanding the pv of a growing annuity formula is critical for financial planning. The example highlights the importance of considering future growth when valuing a stream of payments. Using the pv of a growing annuity formula, investors and financial analysts can make informed decisions about investments, projects, and long-term financial goals. Accurate application of this formula requires careful attention to detail and a thorough understanding of each variable. The use of this formula is key to analyzing the value of investments and other financial assets that generate growing income streams. Mastering the pv of a growing annuity formula is a valuable skill for anyone involved in financial decision-making.
Understanding the Variables: Rate, Growth, and Time
The pv of a growing annuity formula relies heavily on three key variables: the interest rate (r), the growth rate (g), and the number of periods (n). Understanding how each impacts the present value is crucial for accurate calculations and financial planning. The interest rate represents the discount rate used to determine the present value of future cash flows. A higher interest rate reduces the present value, as future payments are worth less today. Conversely, a lower interest rate increases the present value. This is because a lower discount rate means the future cash flows are not discounted as heavily.
The growth rate (g) reflects the annual increase in annuity payments. A higher growth rate increases the present value of the growing annuity, as future payments are larger. Conversely, a lower growth rate decreases the present value. It is important to note that the growth rate should always be less than the interest rate (g < r). If the growth rate exceeds the interest rate, the pv of a growing annuity formula yields a negative or undefined result. This reflects the unrealistic scenario where the payments grow faster than the ability to discount their future value.
The number of periods (n) represents the total number of payments in the annuity. Increasing the number of periods increases the present value, as more payments contribute to the overall value. Conversely, decreasing the number of periods reduces the present value. The interplay between these three variables—interest rate, growth rate, and number of periods—is critical when applying the pv of a growing annuity formula. Sensitivity analysis, which involves examining the effect of small changes in each variable on the present value, highlights the significant impact even minor adjustments can have on the final result. For instance, a small increase in the interest rate might significantly decrease the calculated present value, emphasizing the need for precise input values and a clear understanding of their implications. Mastering this sensitivity analysis is essential for making sound financial decisions based on the pv of a growing annuity formula.
Common Mistakes to Avoid When Using the PV of a Growing Annuity Formula
One common mistake when working with the pv of a growing annuity formula involves misinterpreting the growth rate (g). This rate represents the constant percentage increase in payments each period. Using a nominal growth rate when the effective growth rate is appropriate will lead to an inaccurate present value calculation. Always ensure the growth rate aligns with the compounding frequency of the interest rate. Carefully examine the problem statement to determine the correct growth rate to utilize in the pv of a growing annuity formula.
Another frequent error stems from incorrectly applying the order of operations within the pv of a growing annuity formula. Remember to follow the standard rules of mathematics (PEMDAS/BODMAS), prioritizing calculations within parentheses before performing division and subtraction. Incorrect sequencing will inevitably result in an erroneous present value. Double-check each step to ensure accurate calculation of the pv of a growing annuity formula. Using a calculator or spreadsheet software can help mitigate this risk. The pv of a growing annuity formula requires precision in its application.
Finally, confusion between nominal and effective interest rates is a significant source of errors. The pv of a growing annuity formula requires the use of the effective interest rate. If the problem provides a nominal rate, it must be converted to an effective rate that reflects the actual interest earned considering compounding frequency. Failure to make this conversion will result in a miscalculation of the present value. Clearly identify whether the provided rate is nominal or effective; if nominal, apply the appropriate conversion formula before using the pv of a growing annuity formula. Accurate use of the pv of a growing annuity formula depends on correct input values.
Applying the pv of a growing annuity formula in Diverse Scenarios
The pv of a growing annuity formula proves invaluable in various financial situations beyond the basic examples. Consider an investor evaluating a real estate investment trust (REIT). REITs often distribute dividends that increase over time, reflecting the growth of their underlying properties. Using the pv of a growing annuity formula, the investor can accurately assess the present value of the expected future dividend stream, informing their investment decision. This calculation considers the projected dividend growth rate, the required rate of return, and the investment’s expected lifespan. The formula provides a more comprehensive valuation compared to methods that ignore the growth component.
Another application lies in retirement planning. Instead of assuming a constant annual income in retirement, a more realistic approach incorporates an inflation adjustment. Using the pv of a growing annuity formula, individuals can calculate the present value of their required retirement income, accounting for anticipated increases in living expenses. This helps determine the necessary savings target to maintain a desired living standard throughout retirement. The formula helps tailor savings strategies to inflation’s impact on future needs. Accurate prediction of future retirement income relies heavily on correctly estimating the growth rate of expenses.
Furthermore, the pv of a growing annuity formula finds use in valuing businesses with consistently growing earnings. Instead of simply discounting future earnings at a constant rate, a growing annuity model acknowledges that profitable companies often experience earnings growth. By incorporating a realistic growth rate into the calculation, a more accurate business valuation emerges. This approach allows for a more nuanced understanding of a company’s true worth and enhances investment decisions. The flexibility of the pv of a growing annuity formula makes it adaptable to various business models and growth trajectories. This ensures a more informed assessment of future cash flows and a more precise valuation.
Advanced Considerations and Extensions of the pv of a growing annuity formula
While the standard pv of a growing annuity formula provides a robust tool for valuation, more sophisticated scenarios may require adjustments. For instance, the formula assumes a constant growth rate. In reality, growth rates often fluctuate. Analyzing scenarios with variable growth requires more complex models, potentially involving numerical methods or iterative calculations. These advanced techniques are beyond the scope of this introductory guide, but understanding their existence is crucial for those working with more intricate financial situations. The pv of a growing annuity formula’s limitations become apparent when considering more complex scenarios.
Another area for expansion is the treatment of compounding. The formula presented utilizes discrete compounding, where interest is calculated at specific intervals. Continuous compounding, where interest is calculated constantly, offers a more precise, though more mathematically involved, approach. The transition to continuous compounding necessitates a slightly modified formula. While understanding the theoretical differences is important, practical implications often remain marginal for many typical applications of the pv of a growing annuity formula. The shift from discrete to continuous compounding provides greater accuracy but adds complexity.
Finally, the pv of a growing annuity formula assumes payments occur at the end of each period (ordinary annuity). However, some annuities involve payments at the beginning of each period (annuity due). The calculation for an annuity due differs slightly. This adjustment incorporates the time value of money more accurately for these scenarios, affecting the overall present value calculation. Adapting the formula to account for these different payment schedules remains critical for obtaining reliable valuations using the pv of a growing annuity formula. Understanding these variations ensures accurate financial analysis.