Understanding the Basics of Call Options
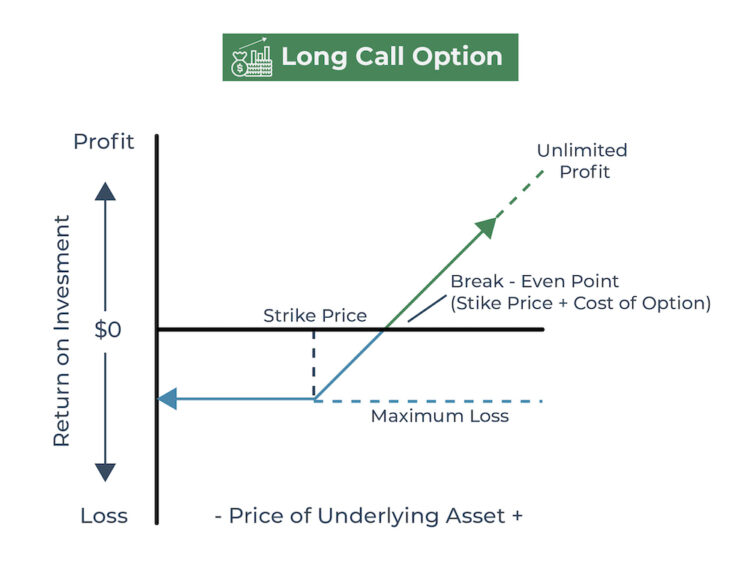
In the world of options trading, call options are a popular investment vehicle that allows traders to capitalize on the potential upside of a security’s price movement. A call option gives the buyer the right, but not the obligation, to purchase an underlying asset at a predetermined price, known as the strike price, before a specified expiration date. This flexibility makes call options an attractive tool for investors seeking to manage risk, speculate on price movements, or generate income.
One of the primary benefits of call options is their ability to provide leverage, allowing traders to control a larger position with a smaller amount of capital. Additionally, call options can be used to hedge against potential losses in a portfolio, providing a level of protection against market volatility. To fully understand the potential of call options, it’s essential to grasp the underlying mechanics of their pricing, including the price of a call option formula, which will be explored in detail later in this guide.
How to Calculate the Price of a Call Option: A Step-by-Step Approach
The Black-Scholes model is a widely used mathematical formula for calculating the price of a call option. Developed by Fischer Black and Myron Scholes in 1973, this model provides a framework for estimating the value of a call option based on several key variables. The formula for the Black-Scholes model is:
C = SN(d1) – Ke^(-rt)N(d2)
Where:
- C = the price of the call option
- S = the current stock price
- K = the strike price
- r = the risk-free interest rate
- t = the time to expiration
- N(d1) and N(d2) = the cumulative distribution functions of the standard normal distribution
- d1 and d2 = variables that can be calculated using the following formulas:
- d1 = ln(S/K) + (r + σ^2/2)t / σ√t
- d2 = d1 – σ√t
The Black-Scholes model takes into account the underlying stock price, strike price, risk-free interest rate, time to expiration, and volatility to estimate the price of a call option. By understanding how to apply this formula, investors can gain a deeper appreciation for the factors that influence the price of a call option formula and make more informed investment decisions.
The Role of Volatility in Call Option Pricing
Volatility is a critical component in the calculation of the price of a call option formula. It represents the extent to which the underlying asset’s price fluctuates over a given period. In the context of options trading, volatility is often referred to as the “fear factor” because it reflects the market’s uncertainty about the future direction of the underlying asset’s price.
A higher volatility means that the underlying asset’s price is more likely to fluctuate rapidly, making it more difficult to predict its future value. As a result, the price of a call option will increase with higher volatility, as the option buyer is willing to pay a premium for the potential upside. Conversely, a lower volatility will result in a lower call option price, as the option buyer is less likely to benefit from significant price movements.
The impact of volatility on call option prices can be seen in the Black-Scholes model, where it is represented by the symbol σ (sigma). An increase in σ will result in a higher call option price, while a decrease in σ will result in a lower call option price. This is because the model takes into account the probability of the underlying asset’s price reaching the strike price at expiration, which is affected by the level of volatility.
Understanding the role of volatility in call option pricing is essential for investors, as it can help them make more informed investment decisions. By recognizing the impact of volatility on the price of a call option formula, investors can adjust their strategies to take advantage of market conditions and maximize their returns.
The Effect of Time Decay on Call Option Prices
Time decay is a critical concept in options trading that refers to the gradual decline in the value of an option over time. As the expiration date approaches, the option’s value decreases, making it less valuable to the buyer. This phenomenon is also known as theta, which represents the rate of decline in the option’s value due to the passage of time.
The effect of time decay on call option prices is significant, as it can erode the value of the option even if the underlying asset’s price remains unchanged. This is because the option buyer is paying a premium for the right to buy the underlying asset at a specified price, and as the expiration date approaches, the likelihood of the option expiring in the money decreases.
The price of a call option formula takes into account the time decay factor, which is reflected in the Black-Scholes model. The model assumes that the option’s value will decrease over time, and this decrease is accelerated as the expiration date approaches. As a result, the price of a call option will decrease as the time to expiration decreases, all other factors being equal.
Understanding the effect of time decay on call option prices is essential for investors, as it can help them make more informed investment decisions. By recognizing the impact of time decay on the price of a call option formula, investors can adjust their strategies to take advantage of market conditions and maximize their returns. For example, investors may choose to sell call options with a shorter time to expiration to take advantage of the time decay factor, or they may opt for longer-term options to give themselves more time to benefit from potential price movements.
Interest Rates and Call Option Pricing: What’s the Connection?
Interest rates play a crucial role in the pricing of call options, as they affect the underlying asset’s value and the option’s premium. The relationship between interest rates and call option prices is complex, but understanding it is essential for investors to make informed investment decisions.
In the Black-Scholes model, the risk-free interest rate is one of the key variables used to calculate the price of a call option formula. The model assumes that the option buyer can earn a risk-free return by investing in a risk-free asset, such as a U.S. Treasury bond. As a result, the option buyer will demand a higher premium for the call option if interest rates are high, as they can earn a higher return from a risk-free investment.
The impact of interest rates on call option prices can be seen in the following ways: an increase in interest rates will result in a higher call option price, while a decrease in interest rates will result in a lower call option price. This is because higher interest rates increase the opportunity cost of holding the underlying asset, making the call option more valuable. Conversely, lower interest rates decrease the opportunity cost, making the call option less valuable.
In addition to the risk-free interest rate, the yield curve also plays a role in call option pricing. The yield curve represents the relationship between interest rates and time to maturity, and it can affect the price of a call option formula. For example, a steepening yield curve can increase the price of a call option, as it indicates higher interest rates in the future, which can increase the underlying asset’s value.
Understanding the connection between interest rates and call option prices is essential for investors, as it can help them make more informed investment decisions. By recognizing the impact of interest rates on the price of a call option formula, investors can adjust their strategies to take advantage of market conditions and maximize their returns.
Real-World Examples of Call Option Pricing in Action
Understanding the price of a call option formula is essential for investors, but seeing it in action can help solidify the concept. In this section, we’ll explore real-world examples of call option pricing in action, including case studies and hypothetical examples.
Example 1: Tech Stock Call Option
Let’s say a tech company, XYZ Inc., is trading at $50 per share. An investor buys a call option to purchase 100 shares of XYZ Inc. at $55 per share, with an expiration date in three months. The price of the call option formula is calculated using the Black-Scholes model, taking into account the underlying asset’s price, volatility, time to expiration, and interest rates. The calculated price of the call option is $2.50 per share.
In this scenario, the investor is betting that the price of XYZ Inc. will rise above $55 per share within the next three months. If the price does rise, the investor can exercise the call option and buy the shares at $55, selling them at the higher market price to profit. If the price doesn’t rise, the option will expire worthless, and the investor will lose the premium paid for the option.
Example 2: Index Call Option
Another example is an index call option on the S&P 500 index. An investor buys a call option to purchase the S&P 500 index at 3,500, with an expiration date in six months. The price of the call option formula is calculated using the Black-Scholes model, taking into account the index’s current value, volatility, time to expiration, and interest rates. The calculated price of the call option is $150 per contract.
In this scenario, the investor is betting that the S&P 500 index will rise above 3,500 within the next six months. If the index does rise, the investor can exercise the call option and buy the index at 3,500, selling it at the higher market price to profit. If the index doesn’t rise, the option will expire worthless, and the investor will lose the premium paid for the option.
These examples demonstrate how the price of a call option formula is used in real-world trading scenarios. By understanding how to calculate the price of a call option, investors can make more informed investment decisions and maximize their returns.
Common Mistakes to Avoid When Calculating Call Option Prices
Calculating the price of a call option formula can be complex, and even experienced investors can make mistakes. In this section, we’ll highlight common errors or misconceptions investors make when calculating call option prices, including tips on how to avoid these mistakes.
Mistake 1: Ignoring Volatility
One common mistake investors make is ignoring the impact of volatility on call option prices. Volatility can significantly affect the price of a call option, and failing to account for it can lead to inaccurate calculations. To avoid this mistake, investors should always consider the underlying asset’s volatility when calculating the price of a call option formula.
Mistake 2: Misusing the Black-Scholes Model
The Black-Scholes model is a widely used formula for calculating the price of a call option, but it’s not a one-size-fits-all solution. Investors should understand the assumptions and limitations of the model and adjust it according to their specific needs. For example, the model assumes a constant volatility, which may not always be the case in real-world markets.
Mistake 3: Failing to Account for Time Decay
Time decay is a critical factor in call option pricing, as it affects the option’s value over time. Investors should always consider the time to expiration when calculating the price of a call option formula, as it can significantly impact the option’s value.
Mistake 4: Overlooking Interest Rates
Interest rates can also impact the price of a call option, and investors should consider them when calculating the price of a call option formula. Failing to account for interest rates can lead to inaccurate calculations and poor investment decisions.
Tips for Avoiding Mistakes
To avoid these common mistakes, investors should:
- Always consider the underlying asset’s volatility, time to expiration, and interest rates when calculating the price of a call option formula.
- Understand the assumptions and limitations of the Black-Scholes model and adjust it according to their specific needs.
- Use real-world examples and case studies to test their calculations and refine their strategies.
- Stay up-to-date with market trends and news to ensure their calculations are accurate and relevant.
By avoiding these common mistakes, investors can ensure accurate calculations and make informed investment decisions when using call options in their portfolios.
Advanced Call Option Pricing Strategies for Experienced Traders
For experienced traders, mastering the price of a call option formula is just the beginning. In this section, we’ll explore advanced strategies for using call options in combination with other derivatives or investment vehicles to maximize returns and minimize risk.
Strategy 1: Call Option Spreads
A call option spread involves buying and selling call options with different strike prices or expiration dates. This strategy can help traders profit from volatility or time decay, while limiting their exposure to potential losses. For example, a trader might buy a call option with a higher strike price and sell a call option with a lower strike price, profiting from the difference in premiums.
Strategy 2: Call Option Collars
A call option collar involves buying a call option and selling a put option with the same underlying asset and strike price. This strategy can help traders hedge against potential losses while still benefiting from upside potential. For example, a trader might buy a call option on a stock and sell a put option on the same stock, limiting their potential losses while still profiting from a potential price increase.
Strategy 3: Call Option Ladders
A call option ladder involves buying and selling call options with different strike prices, creating a “ladder” of potential profits. This strategy can help traders profit from volatility or time decay, while limiting their exposure to potential losses. For example, a trader might buy a call option with a lower strike price and sell a call option with a higher strike price, profiting from the difference in premiums.
Strategy 4: Call Option Ratio Backspreads
A call option ratio backspread involves buying and selling call options with different ratios, creating a “backspread” of potential profits. This strategy can help traders profit from volatility or time decay, while limiting their exposure to potential losses. For example, a trader might buy two call options with a lower strike price and sell one call option with a higher strike price, profiting from the difference in premiums.
By incorporating these advanced strategies into their trading repertoire, experienced traders can take their call option pricing skills to the next level, maximizing their returns and minimizing their risk.

:max_bytes(150000):strip_icc()/call-option-4199998-ddd54a71fc9a479f9dda9e5b9943d9c4.jpg)

:max_bytes(150000):strip_icc()/dotdash_Final_Understanding_How_Options_Are_Priced_Aug_2020-01-c5699fc51f48461fa3413e4e97049857.jpg)
:max_bytes(150000):strip_icc()/dotdash_v3_Understanding_the_Binomial_Option_Pricing_Model_Nov_2020-01-204c5d0f3c5d476a8537fc08f0ecdc55.jpg)