Positively Skewed Distribution and Negatively Skewed Distribution

What is a Skewed Distribution?

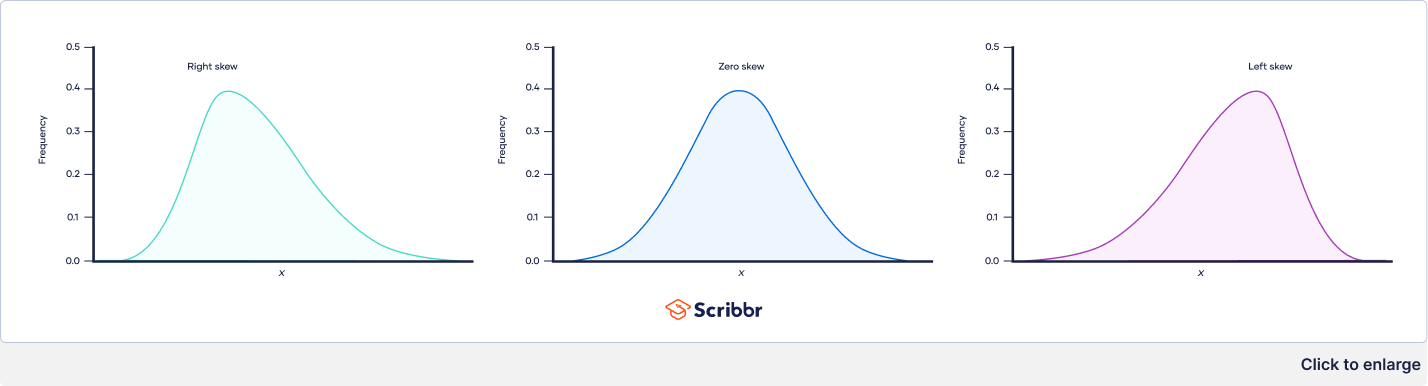
A skewed distribution is a type of probability distribution where the data is not symmetrically distributed around the mean. Unlike a normal distribution, which is bell-shaped and symmetrical, a skewed distribution has a tail that extends longer on one side than the other. This asymmetry indicates that the data is concentrated more on one side of the mean. A simple graph can illustrate this difference clearly: imagine a bell curve for a normal distribution versus a curve stretched out to the right or left. This asymmetry in data distribution, indicating data clustering, is crucial for accurate interpretation. We classify skewed distributions into two main types: positively skewed distributions and negatively skewed distributions. Understanding the nature of this skew is key to data analysis. A positively skewed distribution shows a long tail extending to the right, indicating a higher concentration of data points at lower values. Conversely, a negatively skewed distribution displays a long tail extending to the left, suggesting a clustering of data points at higher values. Both positively skewed distribution and negatively skewed distribution types provide unique insights into the underlying data patterns.

The presence of skewness significantly impacts how data is interpreted. For example, a positively skewed distribution of income might suggest a greater concentration of individuals earning lower incomes, with fewer individuals earning very high incomes. The long tail represents these high earners. The mean, median, and mode will not be equal in a skewed distribution, unlike in a symmetrical distribution. This difference is vital when making inferences from data. Data points, particularly outliers, significantly influence the mean in skewed data. The median proves a more robust measure of central tendency when dealing with positively skewed distribution and negatively skewed distribution. Understanding these characteristics allows for more precise interpretations and avoid misleading conclusions drawn from skewed data sets. A visual representation, like a histogram or box plot, makes it easier to see the asymmetry and thus, the skew.

Visual inspection is a fundamental first step in detecting skewness. Histograms clearly show the distribution shape, while box plots highlight the median and quartiles, offering a quick way to spot asymmetry. The skewness coefficient provides a numerical measure of asymmetry, confirming visual observations. This coefficient is a statistical measure that quantifies the degree and direction of the skew. A positive coefficient indicates a positive skew (right-leaning tail), while a negative coefficient suggests a negative skew (left-leaning tail). A coefficient near zero suggests a nearly symmetrical distribution. However, remember that both positively skewed distribution and negatively skewed distribution can occur in various contexts, and their proper identification is essential for appropriate statistical analysis and sound data interpretation. The proper identification of the distribution type, positively skewed distribution or negatively skewed distribution, is crucial for accurate conclusions from your analysis.

Identifying Skewness in Your Data: Visual Inspection and Measures

Visual inspection is the first step in identifying skewed distributions. Histograms provide a clear picture of the data’s distribution. A positively skewed distribution shows a long tail extending to the right, indicating a concentration of data points at lower values and a few extreme high values. Conversely, a negatively skewed distribution displays a long tail extending to the left, signifying a concentration of data points at higher values with a few extreme low values. Box plots offer another effective visualization tool. The median, quartiles, and outliers are clearly displayed, revealing the symmetry or asymmetry of the data. A longer whisker on one side of the box compared to the other indicates skewness; a longer right whisker suggests a positively skewed distribution, while a longer left whisker points towards a negatively skewed distribution. Examples of positively skewed distributions include income levels, where most people earn modest incomes but a few earn exceptionally high salaries. Negatively skewed distributions are illustrated by exam scores on an easy test, where most students achieve high scores, with fewer students receiving lower marks. These visual representations quickly highlight the difference between a symmetrical distribution and a positively skewed distribution and a negatively skewed distribution.

Beyond visual inspection, statistical measures offer a more quantitative assessment of skewness. The skewness coefficient is a common metric. A positive skewness coefficient indicates a positively skewed distribution, while a negative coefficient suggests a negatively skewed distribution. A coefficient close to zero suggests a roughly symmetrical distribution. It is important to note that the skewness coefficient is sensitive to outliers; extreme values can significantly influence the result. Therefore, visual inspection should always complement the quantitative analysis for a comprehensive understanding. For example, a positively skewed distribution, like house prices, might reveal a higher skewness coefficient due to the presence of luxury properties with significantly higher prices than average. Similarly, a negatively skewed distribution, like the age of death from a specific disease, may show a negative skewness coefficient because of unusually young deaths.

Understanding how to identify skewness is crucial for accurate data interpretation. Both visual methods using histograms and box plots, and the quantitative skewness coefficient provide valuable insights into the nature of the data. The combination of these approaches offers a robust method for detecting and characterizing positively skewed distributions and negatively skewed distributions. Recognizing the presence and direction of skewness helps researchers select appropriate statistical methods and avoid misinterpretations of the data. Misinterpreting a positively skewed distribution, for example, could lead to inaccurate conclusions about the central tendency of the data if the mean is used instead of the median. Using the right method— visual inspection and the skewness coefficient—is key to understanding the true nature of your data.

Positive Skew: What it Means and Where You Find It

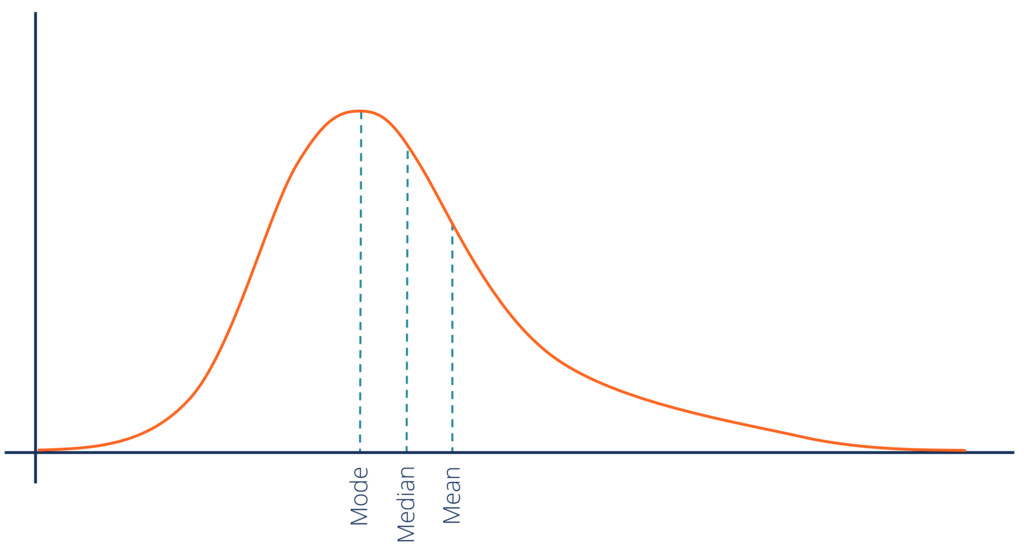
A positively skewed distribution, also known as a right-skewed distribution, is characterized by a long tail extending to the right. This indicates that the majority of data points are concentrated towards the lower end of the distribution, while a smaller number of data points have significantly higher values. The mean is typically greater than the median and mode in a positively skewed distribution. This is because the few high values pull the mean upward, while the median and mode are less sensitive to these outliers. Understanding positively skewed distribution is crucial for accurate data interpretation. This type of skew is common in various real-world scenarios.

House prices provide a classic example of a positively skewed distribution. Most houses fall within a certain price range, but a few luxury homes command extraordinarily high prices. This creates a long right tail. Similarly, income distribution often exhibits positive skew. The majority of individuals earn within a specific income bracket, but a small percentage of high-earners significantly inflate the average income. Understanding this skewness is vital for economic analysis and social policy decisions. Other examples include waiting times in a queue where most people have short waits but a few experience exceptionally long delays, or the distribution of company sizes where a few large corporations dominate while the vast majority are small or medium-sized enterprises. These examples illustrate how positively skewed distributions and negatively skewed distributions frequently appear in different contexts.

The occurrence of positive skew often stems from natural constraints at the lower end of the distribution and unlimited potential at the higher end. For instance, house prices cannot realistically fall below zero, but there is no theoretical upper limit. Similarly, income cannot be negative, but the potential for extremely high earnings exists. This inherent asymmetry leads to the characteristic long right tail. Recognizing this underlying pattern is key to accurately interpreting and analyzing positively skewed data. A thorough grasp of both positively skewed distribution and negatively skewed distribution is critical for effective data analysis across numerous disciplines.

Negative Skew: Understanding the Left-Tail Distribution

Negative skew, in contrast to a positively skewed distribution, describes a distribution where the tail extends to the left. This means that the majority of data points cluster towards higher values, with a smaller number of data points spread out at lower values. Unlike a symmetrical distribution or a positively skewed distribution, the mean in a negatively skewed distribution is typically less than the median and mode. The asymmetry is evident in a histogram, showing a longer tail on the left side. Understanding negatively skewed distribution is crucial for accurate data interpretation, as ignoring this asymmetry can lead to flawed conclusions.

Several real-world examples illustrate negative skew. Consider the scores on an exceptionally easy exam. Most students will achieve high scores, creating a cluster at the upper end. A few students might score lower, creating a tail towards the left. Similarly, the age at death in developed countries often displays negative skew. A large proportion of individuals die at older ages, leading to a cluster of data points on the right, while a smaller number die at younger ages, thus forming a left-tail distribution. These examples showcase how negative skew arises when a natural upper limit restricts the highest values but allows for a broader range of lower values, making it a negatively skewed distribution.

Other scenarios that commonly result in negatively skewed distributions include the age of participants in a youth sports league or the time taken to complete an extremely simple task. In these cases, the bulk of observations gather near the higher end, while a few observations trail off to the lower end, which is characteristic of a negatively skewed distribution. Recognizing this pattern in your data is important, and knowing the difference between a positively skewed distribution and negatively skewed distribution is crucial for selecting appropriate statistical methods. Using methods designed for symmetrical distributions on negatively skewed data might lead to misleading results. Understanding the nuances of positively skewed distribution and negatively skewed distribution allows for a more robust and accurate analysis, preventing misinterpretations in various applications.

How to Determine the Type of Skew in Your Data

Determining whether a dataset exhibits a positively skewed distribution or a negatively skewed distribution involves a two-pronged approach: visual inspection and quantitative analysis. Visual inspection utilizes histograms and box plots. Histograms display the frequency distribution, revealing the tail’s direction. A long tail extending to the right indicates a positively skewed distribution, while a long tail to the left signifies a negatively skewed distribution. Box plots visually represent the data’s quartiles, median, and outliers. A positively skewed distribution shows a longer whisker on the right, while a negatively skewed distribution shows a longer whisker on the left. These visual aids provide a quick assessment of the data’s asymmetry. Remember, positively skewed distributions and negatively skewed distributions present distinct visual characteristics.

Quantitative analysis employs the skewness coefficient, a statistical measure that quantifies the degree and direction of asymmetry. A skewness coefficient greater than zero suggests a positively skewed distribution. Conversely, a coefficient less than zero implies a negatively skewed distribution. A coefficient close to zero indicates a nearly symmetrical distribution. While the precise interpretation of the skewness coefficient depends on the specific dataset and the chosen method of calculation, it complements visual inspection, offering a numerical representation of skewness. For example, a histogram showing a clear rightward skew will likely correspond to a positive skewness coefficient. Analyzing both the visual representation and the numerical coefficient gives a more robust understanding. This combined approach helps to confidently identify positively skewed distribution and negatively skewed distribution in your data.

Interpreting the results requires careful consideration. A high positive skewness coefficient, combined with a right-skewed histogram, strongly suggests a positively skewed distribution. Similarly, a strongly negative skewness coefficient, coupled with a left-skewed histogram, indicates a negatively skewed distribution. However, always consider the context of the data. A slightly positive or negative skewness coefficient might not necessitate transformative actions. Understanding the inherent characteristics of the data and the implications of skewness on subsequent analyses guides the decision-making process. Remember that in many real-world scenarios, perfectly symmetrical distributions are rare. The key is to assess the degree of skewness and its potential impact on your analysis. By combining visual inspection with the skewness coefficient, you can effectively determine the type of skew and interpret its significance within the context of your dataset.

The Impact of Skewed Distributions on Statistical Analysis

Skewed distributions significantly affect the results of common statistical analyses. In a positively skewed distribution, the mean is typically greater than the median and mode. This is because the few extremely high values pull the mean upward. Conversely, in a negatively skewed distribution, the mean is usually less than the median and mode. The influence of a few extremely low values lowers the mean. Understanding this difference is crucial for interpreting data correctly. For instance, in a positively skewed distribution like household income, using the mean to represent average income can be misleading, as it’s inflated by high earners. The median would offer a more representative measure of central tendency in such cases. A positively skewed distribution and negatively skewed distribution both require careful consideration when choosing summary statistics.

The choice of statistical methods also requires careful consideration when dealing with skewed data. Many standard statistical tests assume a normal (symmetrical) distribution. Applying these methods to heavily skewed data can lead to inaccurate results and flawed conclusions. For example, t-tests and ANOVA, which are sensitive to outliers common in positively skewed distribution and negatively skewed distribution, may produce misleading p-values. Therefore, using non-parametric methods, which are less sensitive to deviations from normality, is often more appropriate when analyzing data from positively skewed distributions and negatively skewed distributions. These methods rely on ranks rather than raw data values, making them robust against outliers and skewed data.

Beyond choosing appropriate statistical tests, addressing skewness itself can improve analysis. Transforming the data, such as using a logarithmic transformation, can sometimes make the data more symmetrical and closer to a normal distribution. This allows for the use of parametric methods that are often more powerful and provide more nuanced insights. However, transformations should be applied cautiously, as they can distort the original data and impact interpretation. Remember, the goal is to choose methods and transformations that accurately reflect the underlying patterns in the data, regardless of whether it follows a positively skewed distribution or a negatively skewed distribution. Ignoring the implications of skewed data can lead to misinterpretations and erroneous conclusions.

Real-World Applications and Examples of Skewed Distributions Across Fields

Skewed distributions are prevalent across numerous fields. In finance, investment returns often exhibit a positively skewed distribution. Large gains are less frequent than small losses, creating a long right tail. Conversely, the distribution of losses might be negatively skewed, with a few exceptionally large losses outweighing numerous smaller ones. Understanding these distributions is crucial for risk assessment and portfolio management. Ignoring the skewness can lead to inaccurate estimations of risk and potentially disastrous investment decisions. This is especially important when dealing with positively skewed distribution and negatively skewed distribution data.

Healthcare provides another rich landscape for skewed distributions. The distribution of patient recovery times after surgery might be positively skewed, with most patients recovering quickly, but a few experiencing prolonged recovery periods. Similarly, the distribution of hospital stays could exhibit a positive skew, while the distribution of certain disease severities might be negatively skewed. Accurately modeling these skewed distributions is critical for resource allocation and the effective design of healthcare systems. Failure to account for skewness can lead to flawed predictions about patient outcomes and resource needs. Understanding the implications of positively skewed distribution and negatively skewed distribution in this context is paramount for effective healthcare planning.

Psychology also frequently encounters skewed distributions. Reaction times in cognitive experiments often follow a positively skewed distribution, with most responses being fast, while a few exceptionally slow responses form the long tail. Similarly, the distribution of scores on certain personality tests might be negatively skewed, indicating a concentration of high scores. These skewed distributions need to be considered when interpreting the results of psychological research. Using inappropriate statistical methods on data from positively skewed distribution and negatively skewed distribution could lead to misinterpretations, undermining the validity of research findings. Recognizing and addressing the skewness is fundamental for drawing accurate conclusions in psychology and numerous other fields.

Tackling Skewed Data: Transformation Techniques

Dealing with positively skewed distribution and negatively skewed distribution often requires data transformation. These transformations aim to make the data more symmetrical, improving the performance of standard statistical methods that assume normality. One common technique is the logarithmic transformation. This involves taking the logarithm (typically base 10 or natural log) of each data point. Log transformations are particularly effective for positively skewed data where a few extremely high values pull the mean upward. They compress the range of the data, reducing the influence of those extreme values. However, logarithmic transformations cannot be applied to data containing zero or negative values. For such cases, adding a constant to all values before applying the log transformation might be necessary. Remember, this transformation is more useful with positively skewed distributions.

Other transformations can also address skewed data. Square root transformations, for instance, can also reduce the impact of outliers and are suitable for both positively and negatively skewed distributions. Consider cube root transformations too, offering another level of data compression. The choice of transformation depends on the nature and extent of the skewness in the data. Experimentation and visual inspection of the transformed data are essential to determine the best approach. One way to choose is to compare the skewness coefficient before and after applying these transformations. The goal is to achieve a more symmetrical distribution, minimizing skew and leading to more accurate and reliable statistical analyses.

It’s crucial to remember that data transformation alters the original data. While improving the suitability for certain statistical tests, it also changes the interpretation of the results. Any conclusions drawn from transformed data should carefully consider this transformation. For example, if modeling income data with a log transformation, the resulting coefficients relate to the logarithm of income, not income itself. The appropriate back-transformation is necessary for interpreting results in the original units of measurement. Understanding these limitations is crucial when choosing and applying data transformations to positively skewed distribution and negatively skewed distribution. Therefore, careful consideration of the chosen transformation is vital for accurate data analysis and interpretation. Always visually inspect the transformed data to confirm that the transformation effectively reduces skewness.

Understanding the Practical Implications of Skewed Distributions

The presence of a positively skewed distribution or a negatively skewed distribution significantly impacts data analysis and interpretation. Understanding these distributions is crucial for making informed decisions. In a positively skewed distribution, the mean is typically greater than the median, which is greater than the mode. Conversely, in a negatively skewed distribution, the mean is less than the median, which is less than the mode. This difference in central tendency highlights the influence of outliers in skewed data.

Ignoring the skewness in data can lead to inaccurate conclusions and flawed statistical inferences. For example, using the mean as a measure of central tendency in a heavily skewed dataset might be misleading, as it is heavily influenced by extreme values. The median or other robust measures of central tendency provide more reliable representations. Recognizing positively skewed distribution and negatively skewed distribution characteristics allows researchers to select appropriate statistical tests. Techniques like non-parametric tests are less sensitive to violations of normality assumptions often associated with skewed distributions. This ensures the validity and reliability of research findings.

The implications extend beyond descriptive statistics. Many statistical models assume normally distributed data. When dealing with positively skewed distribution and negatively skewed distribution data, transformations like logarithmic transformations or Box-Cox transformations can often normalize the data, making it suitable for these models. However, understanding the limitations of transformations is important to interpret results correctly. Failing to address skewness can lead to biased estimates and incorrect predictions, especially in fields like finance, where accurately modeling risk and return is crucial. Therefore, addressing skewness is vital for obtaining reliable results and ensuring the robustness of analyses involving positively skewed distribution and negatively skewed distribution data.

Understanding the Impact of Skewness on Statistical Analyses

Skewed distributions significantly impact the results of standard statistical analyses. Unlike symmetrical distributions where the mean, median, and mode are equal, skewed distributions show discrepancies. In a positively skewed distribution, the mean is typically greater than the median, which is greater than the mode. Conversely, in a negatively skewed distribution, the mean is less than the median, which is less than the mode. This difference arises because the mean is sensitive to outliers, while the median is more robust. Understanding this behavior is crucial for interpreting data accurately. For example, using the mean to describe income data, which often exhibits a positively skewed distribution, might give a misleadingly high representation of typical income due to the influence of high earners. The median would provide a more representative measure in this scenario. The choice of central tendency measure is thus vital, depending on the nature of the data’s distribution and the research question.

The presence of positively skewed distribution and negatively skewed distribution also affects the interpretation of variability. Measures of dispersion like the standard deviation, which is heavily influenced by outliers, can be inflated in skewed distributions. This can lead to an overestimation of the variability present in the data. Therefore, alternative measures such as the interquartile range (IQR), which describes the spread of the middle 50% of the data, might be more appropriate for data with pronounced skewness. Analyzing the distribution helps select appropriate statistical tests. For instance, parametric tests, which assume a normal distribution, might not be suitable for significantly skewed data. Non-parametric tests, which are less sensitive to distributional assumptions, may be more appropriate. Failing to account for skewness can lead to inaccurate conclusions and unreliable statistical inferences. Recognizing the presence of a positively skewed distribution or a negatively skewed distribution is the first step to mitigate these issues.

Many statistical methods are sensitive to deviations from normality, and skewed data can bias results. The impact extends to regression analysis, where skewed independent or dependent variables can affect the reliability of the model’s coefficients and predictions. Similarly, in hypothesis testing, skewed data can increase the likelihood of Type I (false positive) or Type II (false negative) errors. Addressing skewness, perhaps through transformations or using non-parametric methods, is crucial for ensuring the validity and accuracy of the statistical analysis. Ignoring skewness can lead to flawed interpretations and potentially misleading conclusions, undermining the overall reliability and credibility of the research findings. Proper understanding and handling of skewed data are thus essential for robust and meaningful analysis.