Visualizing Data Spread: A Guide to Skewness
Understanding data distribution is fundamental in statistical analysis. The way data points cluster and spread reveals key insights about the underlying phenomenon being studied. Data distributions can be symmetrical, where the left and right sides mirror each other, or asymmetrical. This symmetry, or lack thereof, is a crucial aspect of data analysis. In symmetrical distributions, measures of central tendency like the mean, median, and mode coincide. However, many real-world datasets exhibit asymmetry, leading to what is known as a skewed distribution. Recognizing and understanding skewness is vital because it impacts the interpretation of data and the selection of appropriate statistical methods. A positive and negatively skewed distribution influences how we understand the average or typical value within the dataset. A positive and negatively skewed distribution requires different approaches to data transformation and modeling.
The presence of asymmetry in a dataset signifies that the values are not evenly distributed around the mean. Instead, they tend to cluster more on one side, creating a tail that stretches out further on either the left or the right. This elongation of the tail is what defines skewness. Recognizing whether a distribution is symmetrical or exhibits a positive and negatively skewed distribution is a crucial first step. This is essential before applying further statistical analysis. Skewness can arise from various factors. These factors include limitations in data collection or inherent characteristics of the population being studied. Failing to account for skewness can lead to incorrect inferences and misleading conclusions. This can particularly be the case when using statistical tests that assume a normal distribution.
Therefore, understanding the concept of data distribution and recognizing the potential for asymmetry is essential for any statistical analysis. A positive and negatively skewed distribution can significantly impact the results and interpretations derived from the data. Skewness provides a deeper insight into the characteristics of the data. This informs the selection of appropriate statistical techniques. This ultimately leads to more accurate and reliable results. Ignoring the skewness in a dataset will lead to incorrect conclusions about the population. It also undermines the validity of statistical models applied to the data. Recognizing the presence of positive and negatively skewed distribution and addressing its effect is critical for rigorous and reliable statistical inference.
What is a Skewed Distribution? Exploring Asymmetry
A skewed distribution is a type of probability distribution where the data is not symmetrically distributed around the mean. Unlike a normal distribution, which exhibits symmetry, a skewed distribution shows a longer tail extending to one side. This asymmetry indicates that the data is concentrated more heavily on one side of the mean, creating an imbalance. Understanding skewed distributions is crucial because they frequently occur in real-world data, impacting the interpretation of results and the choice of appropriate statistical methods. The presence of a skew often signifies underlying processes or factors that are not equally distributed. Analyzing positive and negatively skewed distribution helps in understanding the nature and source of this imbalance.
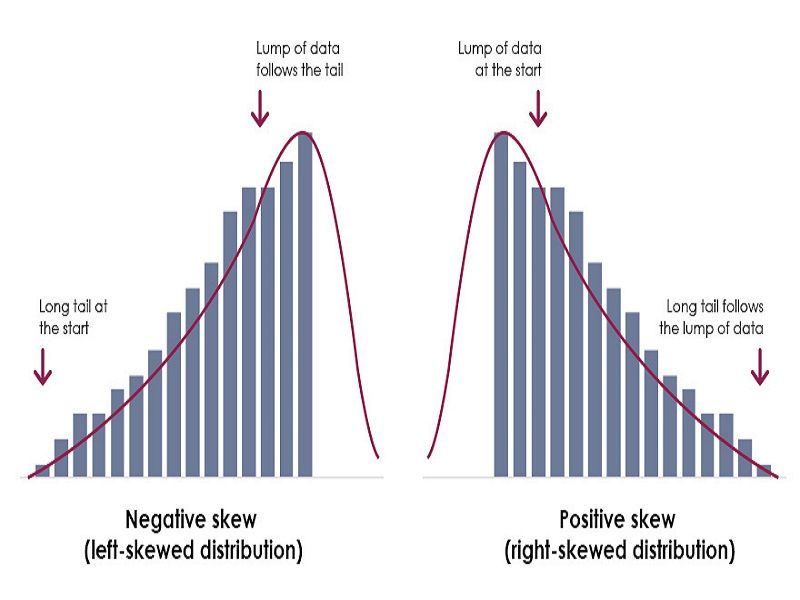
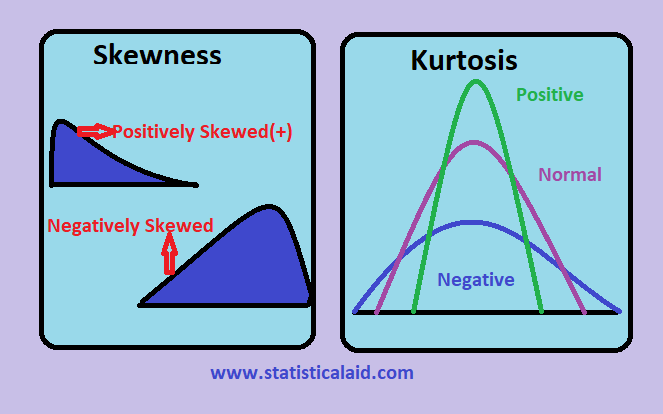
Skewness is quantified to describe the direction and magnitude of the asymmetry. Positive skewness, or right skewness, is characterized by a longer tail on the right side of the distribution. The mean is typically greater than the median in such cases. Conversely, negative skewness, or left skewness, shows a longer tail on the left side, with the mean usually being less than the median. The degree of skewness can range from minimal (nearly symmetrical) to extreme, reflecting the severity of the asymmetry. Many statistical analyses assume a normal distribution, so understanding and addressing skewness is critical for ensuring the validity of results. Dealing with positive and negatively skewed distribution accurately is therefore key for reliable data analysis.
Recognizing and interpreting skewness is vital for accurate data analysis and decision-making. Ignoring skewness can lead to misleading conclusions and inaccurate inferences. Methods exist to mitigate the effects of skewness, such as data transformations. These transformations aim to make the data more closely resemble a normal distribution, allowing for the use of statistical methods that assume normality. Data transformations can improve the reliability and validity of analysis conducted on positive and negatively skewed distribution.
Positive Skew: Identifying Right-Skewed Datasets
Positive skew, also known as right skew, describes a distribution where the tail extends longer on the right side. This indicates a concentration of data points at lower values, with fewer data points scattered at increasingly higher values. The asymmetry is clearly visible; the data is not evenly distributed around a central point. Understanding positive and negatively skewed distribution is crucial for accurate data interpretation. In a positively skewed distribution, the mean is typically greater than the median, and the median is greater than the mode. This is because the few high values pull the mean upwards, while the majority of data points cluster around the lower values, affecting the median and mode. Real-world examples of positively skewed distributions abound. Consider income distribution within a population. A large number of people earn relatively low incomes, while a small number of individuals earn extremely high incomes. This creates a long right tail, characteristic of positive skew. Another example is waiting times in a service queue. Most people might experience relatively short wait times, but a few individuals might encounter exceptionally long delays, again resulting in a positively skewed distribution. The presence of outliers significantly contributes to this type of skew. Properly identifying positive and negatively skewed distribution allows for more accurate statistical analysis and informed decision-making.
Analyzing positive skew involves recognizing the imbalance in data dispersion. The mean, being sensitive to outliers, is pulled towards the longer tail, while the median, less susceptible to extreme values, provides a more robust measure of central tendency. The mode, representing the most frequent value, usually lies closer to the cluster of lower values. The difference between the mean and the median provides a quantitative indicator of the extent of the positive skew. A large positive difference highlights a more pronounced rightward skew. Understanding the implications of positive and negatively skewed distribution is crucial for choosing appropriate statistical methods. For instance, techniques that assume a normal distribution (symmetrical) might yield inaccurate results when applied to positively skewed data. Transformations, such as logarithmic transformations, can help normalize positively skewed data, making it suitable for analyses that rely on normality assumptions. Therefore, careful consideration of the data’s distribution is necessary to ensure the validity and reliability of the subsequent statistical inferences.
The impact of positive skew extends beyond simply visual representation. It affects the reliability of various statistical analyses. For example, the mean, often used to represent central tendency, may be misleading in a positively skewed distribution. The mean is significantly influenced by extreme values, whereas the median and mode give a more representative picture of the central tendency. This is where a comprehensive understanding of positive and negatively skewed distribution becomes extremely important for choosing appropriate analytical techniques. The choice between using the mean, median, or mode often depends on the specific research question and the nature of the data. In positively skewed distributions, the median is often preferred over the mean as a measure of central tendency since it is less affected by outliers. Recognizing and understanding these nuances is crucial for drawing meaningful and accurate conclusions from data analysis, particularly when dealing with datasets that exhibit positive skew.
Negative Skew: Recognizing Left-Skewed Datasets
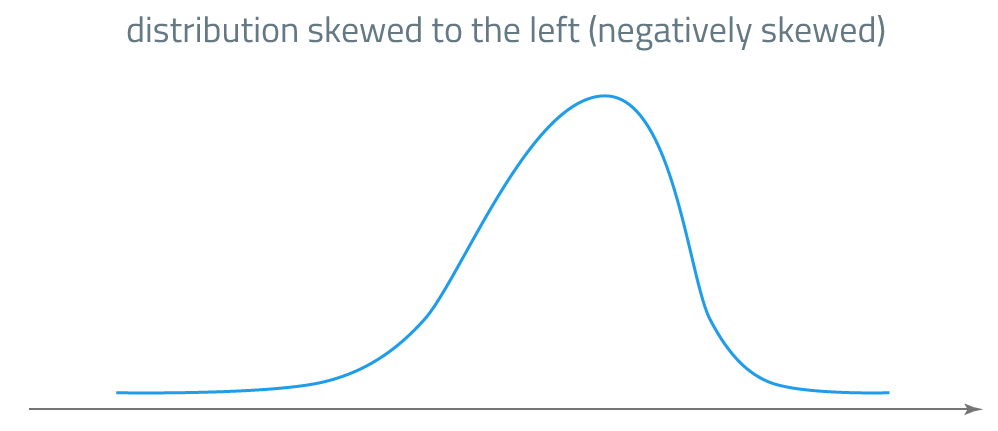
A negatively skewed distribution, also known as a left-skewed distribution, displays a longer tail extending to the left side of the data’s peak. This asymmetry is a key characteristic distinguishing it from a symmetrical or normal distribution. The presence of a leftward skew often indicates that there are some unusually low values in the dataset, pulling the mean toward the left of the data’s central tendency. In a negatively skewed distribution, the mean is typically less than the median.
Consider examples such as age at retirement, where most people retire within a specific age range, resulting in a peak and a relatively small number of people retiring significantly earlier. This concentration of data around a specific value causes a longer tail extending towards lower values and creates a negatively skewed distribution. Similarly, test scores where the majority of students perform well, leading to high scores clustered around a certain range, will exhibit a leftward skew in their distribution. Analyzing such patterns helps one understand the typical behavior and extremes within a dataset, providing valuable insights into the underlying processes or phenomena being studied.
Understanding negative skewness is crucial in interpreting data accurately. Knowing the nature of a distribution, whether symmetrical, positively, or negatively skewed, helps determine the appropriateness of statistical tools for analysis. Recognizing this asymmetry in distributions—positive and negatively skewed distribution—is vital for accurate data interpretation and analysis. Choosing the right methods for analysis depends on the shape of the distribution, and inappropriate selection could lead to inaccurate results. For example, tests assuming a normal distribution may not be reliable when the data has significant skewness.
How to Calculate Skewness: Measuring Asymmetry in Your Data
Calculating skewness involves determining the degree of asymmetry in a distribution. Various methods exist for quantifying this asymmetry, ranging from simple formulas to sophisticated statistical software packages. A crucial aspect of calculating skewness is understanding the underlying principles. The chosen method should effectively reflect the characteristics of the data being analyzed.
One commonly used approach is employing Pearson’s median skewness coefficient. This method leverages the relationship between the mean, median, and standard deviation of the dataset to estimate skewness. This approach offers a straightforward way to assess the symmetry or asymmetry of the data. The formula’s simplicity makes it accessible and applicable across a broad range of datasets. Statistical software packages like Python (with the SciPy library) or R provide functions to calculate skewness effortlessly, automating the process and minimizing potential human error. These tools make it easier to analyze positive and negatively skewed distributions.
For a deeper understanding of positive and negatively skewed distribution, consider exploring other skewness coefficients. Statistical software packages often provide a range of options, catering to different data types and analysis needs. Choosing the right method is essential for accurate results. When working with large datasets or complex distributions, advanced statistical tools might be necessary. Understanding the limitations of specific methods is vital for interpreting the calculated skewness value accurately. Moreover, the calculated skewness value should be interpreted in conjunction with other descriptive statistics and graphical representations to paint a complete picture of the dataset.
Interpreting Skewness Values: What Does the Number Mean?
Interpreting skewness values requires understanding that the magnitude and sign of the skewness coefficient provide insights into the shape of the distribution. A skewness value close to zero suggests a roughly symmetrical distribution, similar to a normal distribution. The data points are evenly distributed around the mean. In such cases, the mean, median, and mode are approximately equal. However, deviations from zero indicate asymmetry. Positive values indicate a positive skew, where the tail extends to the right, while negative values suggest a negative skew, with the tail extending to the left. For positive and negatively skewed distribution, observing the sign is crucial for understanding the direction of the skew.
Rules of thumb exist for classifying the degree of skewness. For example, a skewness value between -0.5 and 0.5 might be considered nearly symmetrical. Values between -0.5 and -1.0, or 0.5 and 1.0, often suggest moderate skewness. Values beyond -1.0 or 1.0 typically indicate high skewness. It’s crucial to remember that these are guidelines, and the appropriate interpretation depends on the specific context and data. Statistical significance testing of skewness can further confirm whether observed asymmetry is statistically meaningful or just due to random variation within the sample. This often involves hypothesis tests, comparing the calculated skewness to a theoretical value under the assumption of symmetry.
Analyzing the relationship between the mean, median, and mode offers additional insights into the type and extent of skewness in positive and negatively skewed distribution. In positively skewed distributions, the mean is typically greater than the median and mode. Conversely, in negatively skewed distributions, the mean is usually smaller than the median and mode. The greater the difference between these measures, the more pronounced the skewness. Understanding these relationships is essential for selecting appropriate statistical methods and interpreting results correctly. The presence of significant skewness may impact the validity of statistical tests that assume normality, potentially leading to inaccurate conclusions if not addressed properly. Methods like data transformations can help mitigate the effects of skewness before proceeding with analyses.
Impact of Skewness: Implications for Statistical Analysis
Skewness significantly impacts the validity and interpretation of statistical analyses. Many common statistical tests, such as t-tests and ANOVAs, assume that the data follows a normal distribution—a symmetrical distribution with zero skewness. When dealing with positive and negatively skewed distributions, these assumptions are violated. This violation can lead to inaccurate results and unreliable conclusions. For instance, a t-test might produce a statistically significant result when it is actually not significant due to the skewed nature of the data. The presence of outliers, often associated with skewed distributions, can further exacerbate this problem. Understanding the impact of skewness is crucial for choosing appropriate statistical methods and interpreting findings correctly. The choice of statistical tests should consider the skewness of the data. Non-parametric methods, which do not rely on normality assumptions, are often preferred when dealing with significantly skewed data.
Data transformations offer a powerful approach to mitigate the effects of skewness. These transformations mathematically alter the data to create a more symmetrical distribution. Common transformations include logarithmic transformations, square root transformations, and reciprocal transformations. The choice of transformation depends on the specific nature of the skewness and the data itself. For example, a logarithmic transformation is frequently used for positively skewed data where many values are clustered near zero and a few are much larger. Applying a suitable transformation can often make the data closer to a normal distribution, enabling the application of parametric tests that assume normality. However, it’s crucial to remember that transformations change the data’s scale, and interpretations must account for this change.
Analyzing positive and negatively skewed distributions requires careful consideration of both the choice of statistical methods and the interpretation of results. The presence of skewness necessitates a critical evaluation of the assumptions underlying any statistical test. Understanding the potential biases introduced by skewness ensures more robust and reliable conclusions. Visual inspection of the data using histograms or box plots is an important first step in identifying skewness. This allows researchers to choose appropriate methods and interpret results more accurately, leading to improved data analysis and decision-making. Failing to address skewness can lead to misinterpretations, potentially influencing important decisions based on flawed analyses.
Skewness and Central Tendency: Mean, Median, and Mode
Understanding the relationship between skewness and measures of central tendency—mean, median, and mode—provides valuable insights into the shape of a distribution. In a symmetrical distribution, the mean, median, and mode are equal. However, this equality is disrupted in positive and negatively skewed distributions. The positions of these three measures relative to each other reveal the direction and magnitude of skewness. For instance, in a positively skewed distribution, the mean is typically greater than the median, which is greater than the mode. This occurs because the long tail on the right pulls the mean towards higher values.
Conversely, in a negatively skewed distribution, the mean is typically less than the median, which is less than the mode. The longer tail on the left side pulls the mean towards lower values. Analyzing the mean, median, and mode together offers a more comprehensive understanding than relying on a single measure. The differences between these measures quantitatively describe the asymmetry present. Consider the income distribution as an example of a positive skew; a few high earners significantly raise the mean income, exceeding the median income earned by the majority. Conversely, a negatively skewed distribution, such as age at retirement, often shows a higher median retirement age compared to the mean due to a few early retirees.
The interplay between skewness and central tendency is crucial for accurate data interpretation. A skewed distribution might lead to misleading conclusions if only the mean is considered. For example, solely reporting the mean income could create a false impression of higher average earnings when the median provides a more representative picture for a positive and negatively skewed distribution. Therefore, analyzing all three measures—mean, median, and mode—is essential for a complete understanding of the data’s central tendency and its degree of asymmetry. This comprehensive approach ensures a more robust and accurate interpretation, particularly when dealing with positive and negatively skewed distributions.