What is a Null Hypothesis and Why Does it Matter?
In multiple regression analysis, a null hypothesis is a crucial concept that plays a central role in statistical inference and hypothesis testing. A null hypothesis, denoted by H0, is a statement that proposes no significant relationship between the independent variables and the dependent variable. In other words, the null hypothesis suggests that the independent variables do not explain the variation in the dependent variable.
The null hypothesis is essential in multiple regression because it provides a basis for testing the significance of the regression coefficients. By formulating a null hypothesis, researchers can determine whether the observed relationships between variables are due to chance or if they reflect a real phenomenon. A well-crafted null hypothesis also helps to avoid false positives, ensuring that the results are not merely a result of chance.
In the context of multiple regression, the null hypothesis is typically tested against an alternative hypothesis, denoted by H1. The alternative hypothesis proposes that there is a significant relationship between the independent variables and the dependent variable. By comparing the null and alternative hypotheses, researchers can determine the probability of observing the results assuming that the null hypothesis is true. This probability, known as the p-value, is a critical component of hypothesis testing in multiple regression.
Formulating a null hypothesis for multiple regression is a critical step in the research process, as it directly impacts the interpretation of the results. A null hypothesis that is poorly formulated or irrelevant to the research question can lead to misleading conclusions and incorrect decisions. Therefore, it is essential to understand the role of the null hypothesis in multiple regression analysis and how to formulate it correctly.
https://www.youtube.com/watch?v=cpL38ZeIecE
How to Formulate a Null Hypothesis for Multiple Regression
Formulating a null hypothesis for multiple regression is a crucial step in the research process. A well-crafted null hypothesis provides a clear direction for the research and ensures that the results are meaningful and relevant. In this section, we will provide a step-by-step guide on how to formulate a null hypothesis for multiple regression.
Step 1: Identify the Research Question
The first step in formulating a null hypothesis is to identify the research question. The research question should be specific, clear, and concise, and it should guide the entire research process. For example, “Is there a significant relationship between the amount of exercise and blood pressure in adults?”
Step 2: Select the Dependent and Independent Variables
The next step is to select the dependent and independent variables. The dependent variable is the outcome variable that we are trying to predict, while the independent variables are the predictor variables that we use to explain the variation in the dependent variable. In our example, the dependent variable is blood pressure, and the independent variable is the amount of exercise.
Step 3: State the Null Hypothesis
The null hypothesis is a statement that proposes no significant relationship between the independent variables and the dependent variable. In our example, the null hypothesis would be “There is no significant relationship between the amount of exercise and blood pressure in adults.” This null hypothesis is denoted by H0.
Step 4: State the Alternative Hypothesis
The alternative hypothesis is a statement that proposes a significant relationship between the independent variables and the dependent variable. In our example, the alternative hypothesis would be “There is a significant relationship between the amount of exercise and blood pressure in adults.” This alternative hypothesis is denoted by H1.
By following these steps, researchers can formulate a clear and concise null hypothesis for multiple regression. A well-crafted null hypothesis provides a clear direction for the research and ensures that the results are meaningful and relevant. In the next section, we will discuss the importance of the null hypothesis in multiple regression modeling.
The Role of Null Hypothesis in Multiple Regression Modeling
In multiple regression modeling, the null hypothesis plays a crucial role in guiding the analysis and interpretation of results. The null hypothesis serves as a benchmark against which the alternative hypothesis is tested, and its formulation has a direct impact on the outcome of the analysis.
The null hypothesis influences model interpretation by determining the significance of the regression coefficients. If the null hypothesis is rejected, it implies that the independent variables have a significant effect on the dependent variable, and the regression coefficients can be used to make predictions. On the other hand, if the null hypothesis is not rejected, it suggests that the independent variables do not have a significant effect on the dependent variable, and the regression coefficients are not reliable.
The null hypothesis also affects coefficient estimation in multiple regression. The null hypothesis is used to test the significance of each regression coefficient, and if the null hypothesis is rejected, the coefficient is considered statistically significant. This, in turn, affects the interpretation of the results, as statistically significant coefficients are used to make predictions and draw conclusions.
Furthermore, the null hypothesis is essential for p-value calculation in multiple regression. The p-value represents the probability of observing the results assuming that the null hypothesis is true. A low p-value indicates that the null hypothesis can be rejected, implying that the independent variables have a significant effect on the dependent variable. A high p-value, on the other hand, suggests that the null hypothesis cannot be rejected, and the independent variables do not have a significant effect on the dependent variable.
In summary, the null hypothesis is a critical component of multiple regression modeling, as it guides the analysis and interpretation of results. Its formulation has a direct impact on model interpretation, coefficient estimation, and p-value calculation. By understanding the role of the null hypothesis in multiple regression, researchers can ensure that their analysis is accurate and reliable, leading to meaningful conclusions and informed decision-making.
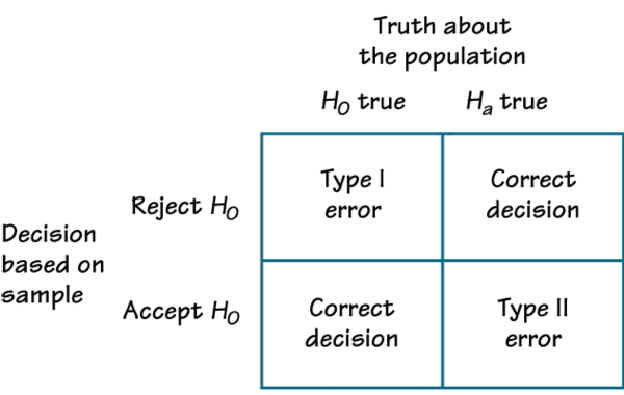
Understanding Type I and Type II Errors in Multiple Regression
In multiple regression analysis, Type I and Type II errors are critical concepts that researchers must understand to ensure accurate and reliable results. These errors occur when testing the null hypothesis, and their consequences can be far-reaching.
A Type I error occurs when the null hypothesis is rejected, but it is actually true. This means that the researcher has incorrectly concluded that there is a significant relationship between the independent variables and the dependent variable. The probability of committing a Type I error is denoted by α (alpha) and is typically set to 0.05. A Type I error can lead to false conclusions and misinformed decision-making.
On the other hand, a Type II error occurs when the null hypothesis is not rejected, but it is actually false. This means that the researcher has failed to detect a significant relationship between the independent variables and the dependent variable. The probability of committing a Type II error is denoted by β (beta) and is related to the power of the test. A Type II error can lead to missed opportunities and incorrect assumptions.
The consequences of committing Type I and Type II errors can be significant. A Type I error can lead to the implementation of ineffective solutions or the allocation of resources to non-essential areas. A Type II error can lead to the failure to identify important relationships or the underestimation of the impact of independent variables.
To minimize the risk of Type I and Type II errors, researchers must carefully formulate the null hypothesis, select an appropriate significance level, and ensure adequate sample size and data quality. By understanding the concepts of Type I and Type II errors, researchers can ensure that their multiple regression analysis is accurate, reliable, and informative.
Interpreting the Results of Multiple Regression Analysis
Once the multiple regression analysis is complete, interpreting the results is crucial to understanding the relationships between the independent variables and the dependent variable. In this section, we will discuss how to interpret the coefficient of determination (R-squared), F-statistic, and p-values.
The coefficient of determination, denoted by R-squared, measures the proportion of variance in the dependent variable that is explained by the independent variables. An R-squared value close to 1 indicates a strong relationship between the independent variables and the dependent variable, while a value close to 0 indicates a weak relationship. In multiple regression analysis, R-squared is used to evaluate the goodness of fit of the model.
The F-statistic is a measure of the overall significance of the regression model. It is used to test the null hypothesis that all the regression coefficients are equal to zero. A high F-statistic value indicates that the regression model is significant, and the independent variables have a significant effect on the dependent variable.
P-values are used to determine the significance of each regression coefficient. A p-value less than the significance level (typically 0.05) indicates that the regression coefficient is statistically significant, and the independent variable has a significant effect on the dependent variable. On the other hand, a p-value greater than the significance level indicates that the regression coefficient is not statistically significant, and the independent variable does not have a significant effect on the dependent variable.
When interpreting the results of multiple regression analysis, it is essential to consider the null hypothesis for multiple regression. The null hypothesis is used to test the significance of the regression coefficients, and its formulation has a direct impact on the interpretation of the results. By understanding the null hypothesis and its role in multiple regression analysis, researchers can ensure that their results are accurate and reliable.
Common Pitfalls to Avoid When Working with Null Hypotheses
When working with null hypotheses in multiple regression analysis, it is essential to avoid common pitfalls that can lead to inaccurate or misleading results. In this section, we will discuss some of the most common mistakes to avoid when working with null hypotheses.
One of the most critical mistakes is incorrect hypothesis formulation. A poorly formulated null hypothesis can lead to incorrect conclusions and misinformed decision-making. To avoid this, researchers must carefully identify the research question, select the dependent and independent variables, and state the null hypothesis clearly and concisely.
Inadequate sample size is another common pitfall. A sample size that is too small can lead to inaccurate estimates of the regression coefficients and p-values, making it difficult to draw meaningful conclusions. Researchers must ensure that the sample size is sufficient to detect significant relationships between the independent variables and the dependent variable.
Misinterpretation of results is also a common mistake. Researchers must be careful not to overinterpret the results of multiple regression analysis, especially when it comes to the null hypothesis. A failure to reject the null hypothesis does not necessarily mean that there is no significant relationship between the independent variables and the dependent variable. Rather, it may indicate that the sample size is too small or the data is too noisy to detect a significant relationship.
Additionally, researchers must avoid ignoring the assumptions of multiple regression analysis. Violating the assumptions of linearity, independence, homoscedasticity, normality, and no or little multicollinearity can lead to inaccurate results and incorrect conclusions. By checking the assumptions of multiple regression analysis, researchers can ensure that the results are reliable and accurate.
Finally, researchers must avoid using multiple regression analysis as a black box. Multiple regression analysis is a powerful tool, but it requires a deep understanding of the underlying statistical concepts and assumptions. By understanding the null hypothesis for multiple regression and its role in statistical inference and hypothesis testing, researchers can ensure that their results are accurate, reliable, and informative.
Real-World Applications of Multiple Regression Analysis
Multiple regression analysis has numerous real-world applications across various fields, including finance, marketing, healthcare, and more. In this section, we will explore some of the most significant applications of multiple regression analysis.
In finance, multiple regression analysis is used to predict stock prices, analyze portfolio risk, and identify factors that influence investment returns. For instance, a financial analyst may use multiple regression to examine the relationship between a company’s stock price and various economic indicators, such as GDP, inflation rate, and unemployment rate.
In marketing, multiple regression analysis is employed to analyze customer behavior, predict sales, and optimize marketing campaigns. Marketers may use multiple regression to identify the factors that influence customer purchasing decisions, such as demographics, advertising spend, and price.
In healthcare, multiple regression analysis is used to identify risk factors for diseases, predict patient outcomes, and evaluate the effectiveness of treatments. For example, a healthcare researcher may use multiple regression to examine the relationship between patient characteristics, such as age, gender, and lifestyle, and the risk of developing a particular disease.
In addition to these fields, multiple regression analysis has applications in economics, social sciences, and environmental studies. It is a powerful tool for analyzing complex relationships between variables and making informed decisions.
In all these applications, the null hypothesis for multiple regression plays a critical role in statistical inference and hypothesis testing. By formulating a clear and concise null hypothesis, researchers can ensure that their results are accurate, reliable, and informative.
By understanding the real-world applications of multiple regression analysis, researchers and practitioners can unlock the full potential of this powerful statistical technique and make data-driven decisions that drive business success and improve lives.
Best Practices for Implementing Multiple Regression in Your Research
When implementing multiple regression in research, it is essential to follow best practices to ensure accurate, reliable, and informative results. In this section, we will discuss some of the most critical best practices for implementing multiple regression in research.
Data Preparation: Before conducting multiple regression analysis, it is crucial to prepare the data properly. This includes checking for missing values, outliers, and multicollinearity, as well as transforming variables to meet the assumptions of multiple regression.
Model Validation: Validating the multiple regression model is critical to ensuring that the results are accurate and reliable. This includes checking the model’s assumptions, such as linearity, independence, homoscedasticity, normality, and no or little multicollinearity.
Result Reporting: When reporting the results of multiple regression analysis, it is essential to provide clear and concise information about the model, including the null hypothesis for multiple regression, the coefficient of determination (R-squared), F-statistic, and p-values.
Interpretation of Results: Interpreting the results of multiple regression analysis requires a deep understanding of the null hypothesis for multiple regression and its role in statistical inference and hypothesis testing. Researchers must be careful not to overinterpret the results, especially when it comes to the null hypothesis.
Avoiding Common Pitfalls: Finally, researchers must avoid common pitfalls when working with null hypotheses in multiple regression, such as incorrect hypothesis formulation, inadequate sample size, and misinterpretation of results.
By following these best practices, researchers can ensure that their multiple regression analysis is accurate, reliable, and informative, and that the results are useful for making informed decisions.
Remember, the null hypothesis for multiple regression is a critical component of statistical inference and hypothesis testing, and it plays a vital role in ensuring that the results of multiple regression analysis are accurate and reliable.