Negative Skew vs Positive Skew

What is Skewness and Why Does It Matter?

Skewness, in essence, is a measure of the asymmetry of a probability distribution. It reveals the extent to which a distribution leans more towards one side, rather than being symmetrical. Understanding skewness is crucial in various analytical fields, including data analysis and statistics. The shape of a distribution, especially when it deviates from symmetry, significantly impacts the interpretation of data, making skewness a vital characteristic to assess. For example, when analyzing test scores or financial data, skewness can distort our understanding of average performance or typical outcomes. Therefore, recognizing and understanding the implications of skewness, such as negative skew vs positive skew, is essential for accurate analysis and interpretation. By considering the skewness of data, analysts can avoid misleading conclusions and make more informed decisions. The presence of positive or negative skew can influence the choice of appropriate statistical methods and models, impacting both the accuracy and the reliability of the findings. In the world of data analysis, being aware of skewness is akin to having a critical lens that allows for a more nuanced and insightful understanding of data patterns. Data distributions are not always symmetrical, which highlights the need for skewness consideration in any data analysis.

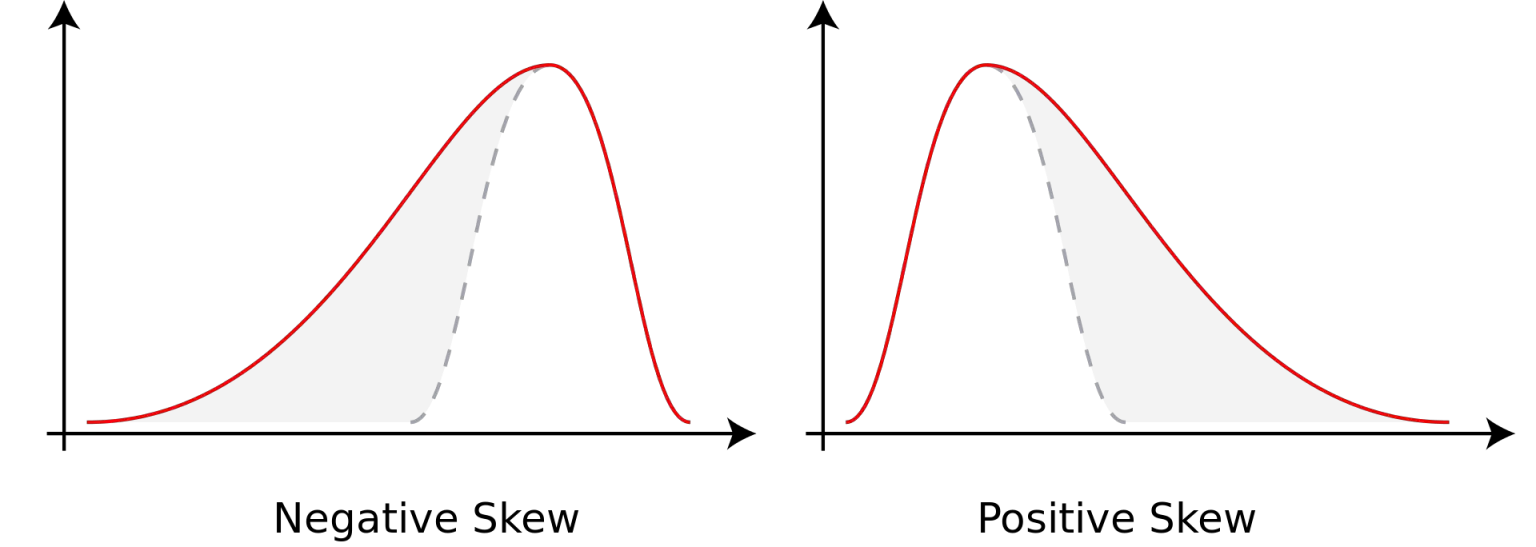
Positive Skew: When the Tail is on the Right

Positive skew, in the context of data distribution, describes a scenario where the tail of the distribution extends towards the right side of the graph. This visual characteristic indicates that a high number of data points are clustered towards the lower end of the values, while fewer data points are found on the higher end. The distribution is not symmetrical; instead, it is stretched towards the right. Imagine a histogram representing this, where the bulk of the bars are concentrated on the left, gradually tapering off to a few smaller bars on the right. This “tail” of the distribution on the right defines a positive skew. Understanding the shape of data is key to compare negative skew vs positive skew.

For example, consider the distribution of incomes in a population. Typically, a large segment of people might earn relatively lower incomes, while a smaller segment earns substantially higher incomes. In a histogram representing this income data, most of the bars would cluster around the lower income ranges (left side of the histogram), and then a long tail would trail toward the higher income ranges (right side), representing the fewer people with high incomes. This demonstrates positive skew. Another example can be found in the context of waiting times, if we look at a queue where the majority of the people experience short waiting times, and a small number of people experience prolonged waiting times, that is also an example of positive skew. In each of these examples, it’s important to note that we focus on the shape of the data distribution, rather than the real-life experience alone. The distinction between negative skew vs positive skew is very important for correct data analysis.

Negative skew, in contrast to positive skew, occurs when the tail of the distribution extends towards the left. This means that the bulk of the data points are concentrated on the right side of the distribution, with fewer values trailing off to the lower end. Visually, a negatively skewed distribution has a longer, thinner tail on its left side, and the highest part of the distribution is situated toward the higher values. To understand negative skew vs positive skew, imagine a scenario of student grades on a very easy test. In this case, a large number of students would likely achieve high scores, creating a cluster of data points on the right side of the distribution. Conversely, only a few students might receive lower scores, creating a tail on the left, showing the negative skew. This illustrates how the data is distributed, with the majority of values towards the higher end and just a few with lower values.

The concept of negative skew can be better understood by contrasting it with positive skew. While positive skew indicates a long tail extending towards the right with more low values, negative skew showcases a tail extending toward the left with a greater concentration of high values. The comparison of negative skew vs positive skew can be further highlighted by their real-world examples. In the case of negative skew, consider the distribution of survival times for patients with a highly effective treatment. Many patients might experience long survival times, represented by the bulk of data points concentrated on the right, whereas only a few might have shorter survival times, forming the tail to the left. So when considering negative skew vs positive skew, the key difference lies in the location of data concentration and the direction of the distribution’s tail.

Key Differences Between Positive and Negative Skew

Understanding the nuances between positive and negative skew is crucial for accurate data interpretation. In a positively skewed distribution, the tail extends towards the right, indicating a concentration of data points on the left side with fewer higher values. Conversely, negative skew presents a distribution where the tail points to the left, signifying a cluster of data towards the right side and fewer lower values. A key difference lies in the relationship between the measures of central tendency. In positive skew, the mean is typically greater than the median, which, in turn, is greater than the mode. This reflects the influence of the high-value outliers pulling the mean towards the right. In contrast, a negative skew exhibits a mean that is less than the median, which is less than the mode, as the lower-value outliers pull the mean towards the left. The impact of skewness also varies. When skewness is minimal, its effect on analysis may be relatively small. However, in severely skewed data sets, the distortion caused by the asymmetry can become significant, leading to potential misinterpretations and inaccurate model outputs. For instance, the difference between negative skew vs positive skew is important in determining the proper statistical approach.

The distinction between the two is further visualized by considering how data is clustered. With positive skew, imagine a histogram where the bulk of the bars are clustered to the left, gradually decreasing in height as you move right, which is often observed in salary distribution data. With negative skew, the opposite occurs; most bars are found to the right with a decreasing tail extending to the left. Negative skew vs positive skew highlights that not only the direction of the tail is different but also the values of mean, median, and mode are positioned differently. When skewness is not addressed, it can mislead statistical analyses and modeling. For example, ignoring the influence of a positive skew in financial data could lead to underestimating risk. Similarly, failing to recognize a negative skew in educational test results might obscure the real challenges faced by a few low-performing students. The degree of skewness significantly affects which types of analyses are suitable. For example, it might be acceptable to ignore slight skewness with large sample sizes, but transformations are often needed when the data exhibits high skewness to avoid flawed conclusions.

In practical terms, data exhibiting a high degree of skewness requires careful consideration. While minimal skewness may have a negligible impact, severe skewness can dramatically affect statistical outcomes. A helpful approach is to always examine the data’s distribution before applying any analytical methods, ensuring that the chosen methods are robust against any distortions caused by skewed distributions. Whether you have negative skew vs positive skew it’s imperative to select appropriate statistical methods or to implement data transformations. Understanding negative skew vs positive skew is, therefore, essential for making sound judgments about data, preventing errors, and ensuring that interpretations are both accurate and relevant to the context of the data. The implications of these differences should be recognized in fields ranging from finance to medical analysis to ensure the insights gained are truly representative of the data.

How to Determine If Your Data Has Skewness

Visual assessment of skewness is often the first step in understanding your data distribution. Histograms are particularly useful; a distribution with a tail extending to the right indicates positive skew, while a tail extending to the left suggests negative skew. Similarly, box plots can reveal skewness through the asymmetry of the box and the length of the whiskers. A longer whisker on the right side hints at positive skew, whereas a longer whisker on the left suggests negative skew. The relative positions of the mean, median, and mode also provide clues about the type of skew. In a positively skewed distribution, the mean is typically greater than the median, which is greater than the mode, as the mean is ‘dragged’ by the extreme values in the tail. Conversely, in a negatively skewed distribution, the mean tends to be less than the median, which is less than the mode. These observations are key in understanding negative skew vs positive skew in your data.

While visual inspection offers an initial understanding, quantitative measures like the skewness coefficient provide a numerical value for the degree and direction of skew. A positive coefficient indicates positive skew, a negative coefficient indicates negative skew, and a coefficient close to zero suggests a relatively symmetrical distribution. There are different formulas to compute the skewness coefficient; some software tools compute it automatically. It’s important to note that with small sample sizes, the calculated skewness might not accurately reflect the true underlying distribution of the population, so interpreting skewness should be done cautiously when you have small sample size, as some extreme values can skew your data. Furthermore, remember that it is important to look for presence of negative skew vs positive skew in your data to choose the right analysis for it.

Context_6: Skewness significantly impacts statistical analysis and modeling, making it crucial to understand its implications. Neglecting the presence of skew, especially when dealing with substantial negative skew vs positive skew, can lead to inaccurate conclusions and flawed decision-making. For instance, in financial analysis, if stock returns are positively skewed, using the mean return as a typical value can be misleading, as the mean would be inflated by a few exceptionally high returns. Conversely, with negatively skewed data, like the time taken to complete a task, neglecting the left-skew could underestimate the proportion of individuals that finish the task quickly. Similarly, regression models built on skewed data might not accurately predict outcomes. The common assumption of normality in many statistical tests can be violated if significant skewness exists, leading to biased and unreliable results. Therefore, recognizing negative skew vs positive skew, and the magnitude of skewness is vital in any statistical evaluation.

To address the challenges posed by skewed data, several techniques can be employed. Data transformation, such as logarithmic or square-root transformations, is often used to reduce the degree of skewness and make the data more suitable for parametric statistical methods that assume a normal distribution. In many cases, the log transformation can normalize the positive skew of the data, as well as reduce the effects of outliers. Another approach involves using non-parametric statistical methods, which do not make assumptions about the underlying distribution of the data, making them more robust to violations of normality. Robust statistical methods, such as the median rather than the mean, can be better choices when the data is skewed, since they are less sensitive to outliers or extreme values. In addition, when using models, care should be taken to use models that can handle skewed data. Failing to account for data skewness can lead to inaccurate forecasting, especially in economics and finance, where there is substantial asymmetry due to the nature of financial markets. For example, option pricing models are highly sensitive to skewness in return distributions, and ignoring this factor can result in inaccurate and unreliable model predictions when dealing with negative skew vs positive skew.

Context_7: Understanding the nuances of negative skew vs positive skew has far-reaching practical applications that extend beyond the realm of statistical analysis into everyday decision-making. In finance, for instance, analyzing investment returns often reveals a positive skew, where most returns are modest with a few instances of significantly high gains. Recognizing this pattern enables investors to better assess risk and potential rewards, influencing strategies for portfolio diversification and asset allocation. Conversely, in fields like performance evaluation in sports, the distribution of times or scores might exhibit a negative skew, indicating that most athletes perform well with only a few achieving significantly lower results. This can influence the way coaches assess talent, design training regimes, and understand an athlete’s progression.

In the medical field, skewness plays an important role when evaluating the impact of a new treatment on patient outcomes. For instance, in clinical trials, a negative skew in a patient’s recovery time may indicate that the treatment is effective for the majority of patients with a few cases of prolonged recovery. Conversely, a positive skew in the duration of an illness might suggest that most patients recover quickly, but some encounter protracted or severe health issues. Understanding such patterns of data distribution are important for accurate interpretations of the efficacy of treatment and the potential risks involved. Furthermore, in economic analysis, income distribution often displays positive skew, where most of the population earns a moderate income, while a small percentage have much higher earnings. Recognizing the skewness of data distributions allows for a more nuanced interpretation of economic metrics such as average income and wealth distribution. In practical situations, a business owner might find the customer rating of a particular product exhibit a negative skew, indicating that most customers are very satisfied, while very few customers have low rating.

These applications underscore the importance of acknowledging and interpreting skewness when assessing data across different domains. The ability to discern between negative skew vs positive skew, not only enhances the accuracy of the statistical analysis, but also enhances the quality of decision-making in real-world scenarios. By understanding the underlying distribution patterns, professionals and individuals alike can make more informed decisions and develop more effective strategies based on the data available to them. Whether analyzing financial markets or evaluating treatment results, awareness of skewness and its potential implications is key for anyone looking to make the best possible outcome.

Conclusion: Choosing the Right Approach Based on Skewness

The distinction between positive and negative skew is crucial for effective data analysis. Positive skew, characterized by a long tail extending towards higher values, indicates that most data points are clustered on the lower end of the distribution. Conversely, negative skew features a tail towards lower values, with the bulk of the data concentrated on the higher end. Understanding this difference is fundamental because it significantly influences the interpretation of statistical measures and the validity of analytical conclusions. Failing to recognize and account for skewness can lead to inaccurate inferences and flawed decision-making. Therefore, correctly identifying whether a dataset exhibits positive skew or negative skew is a critical first step in any data-driven analysis.

Recognizing the presence of either negative skew vs positive skew in a distribution is not just an academic exercise; it has practical implications across numerous fields. In finance, understanding the skewness of returns on investment can affect risk assessment. In the realm of performance evaluation, considering skewness can help provide a more accurate assessment of overall performance. Similarly, in medical studies, accounting for skewness ensures more realistic conclusions about the impact of treatments on patients. Ignoring skewness can lead to underestimating the impact of outlier events, or alternatively, lead to misinterpretations of central tendencies, potentially resulting in poor decisions.

In summary, the concepts of negative skew vs positive skew are vital in data analysis because they shape the way we understand data and thus can dictate the entire analysis process. A proper consideration of data distribution through the lens of skewness ultimately leads to more accurate insights and better decision-making. Therefore, understanding your data’s distribution is a critical first step, influencing the choice of appropriate statistical techniques. The choice of analysis and modeling strategy should always be informed by the shape of the data distribution to avoid misleading results. Careful examination of whether your data exhibits a positive skew or a negative skew will ensure a more accurate, meaningful outcome.