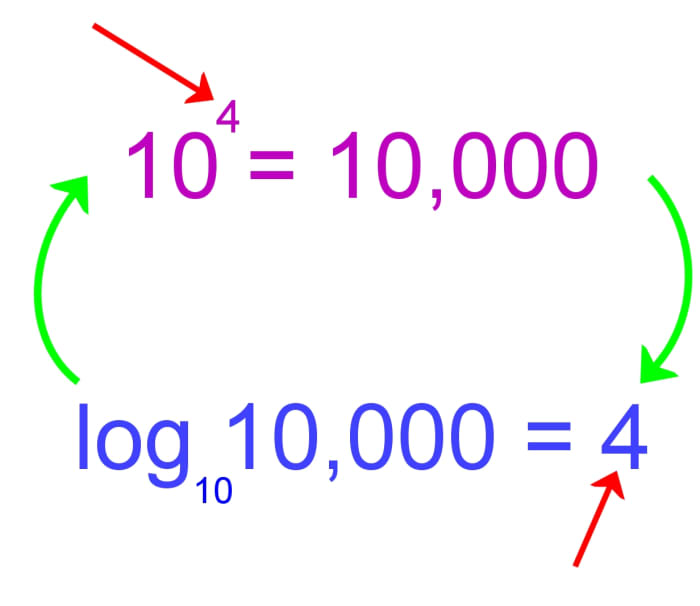Why Logarithmic Conversion Matters
Logarithmic conversion is a fundamental concept in various fields, including mathematics, science, and engineering. It plays a crucial role in simplifying complex calculations and revealing hidden patterns. By learning how to convert to log, professionals and students can unlock new insights and approaches to problem-solving. In mathematics, logarithmic conversion enables the calculation of large numbers and exponential functions, making it an essential tool for algebra and calculus. In science, it helps to model population growth, chemical reactions, and physical phenomena. In engineering, it is used to design electronic circuits, optimize systems, and analyze data. The ability to convert values to their logarithmic equivalents has far-reaching implications, and understanding how to do so can greatly enhance analytical skills and problem-solving abilities.
Understanding Logarithmic Functions: A Brief Refresher
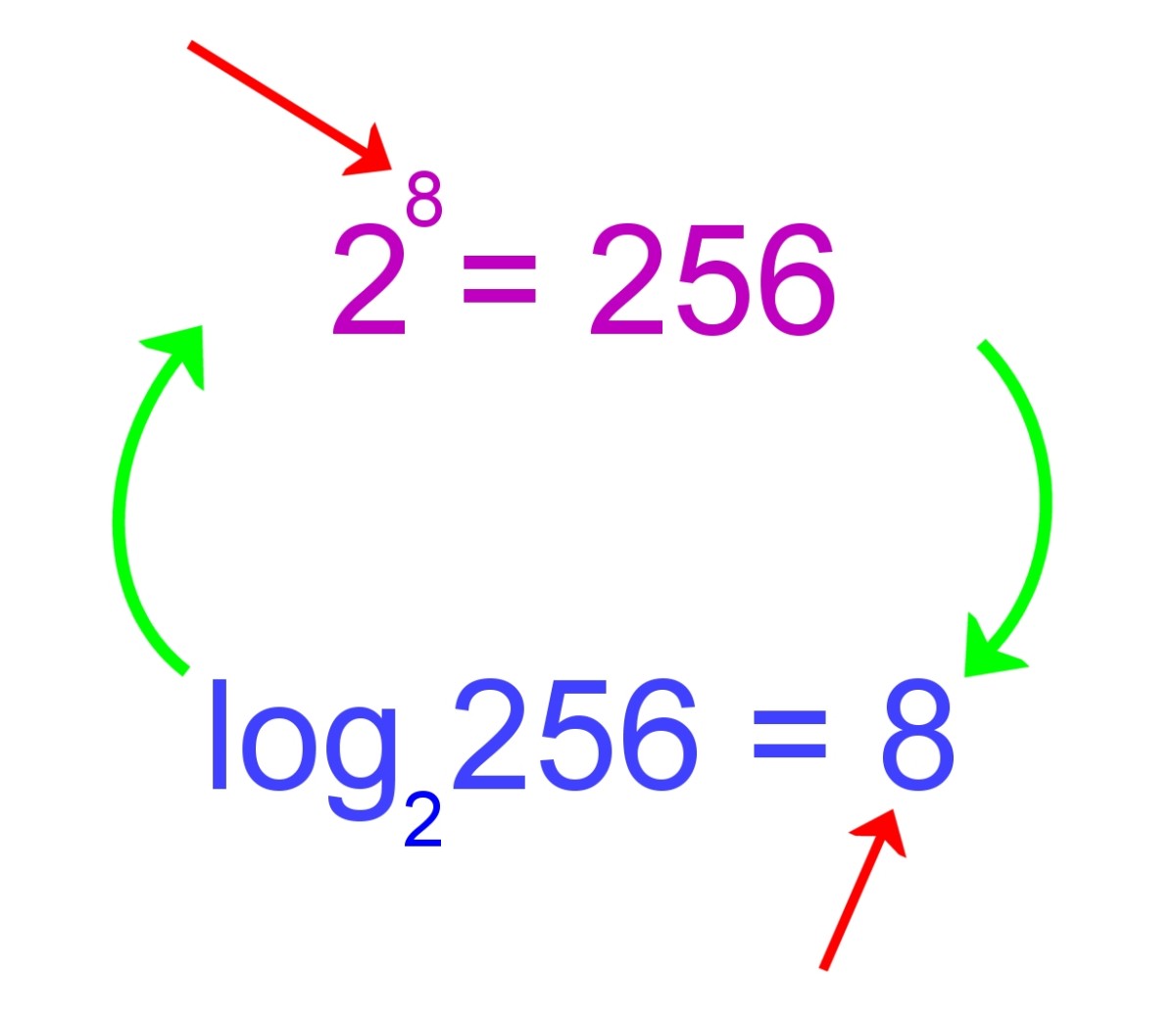
A logarithmic function is the inverse operation of exponentiation, defined as the power to which a base number must be raised to produce a given value. In other words, it is the exponent that satisfies the equation x = b^y, where x is the value, b is the base, and y is the logarithm. There are two common types of logarithmic functions: natural logarithm (ln) and common logarithm (log). The natural logarithm has a base of Euler’s number (e), approximately 2.718, while the common logarithm has a base of 10. Understanding the properties of logarithmic functions, such as the product rule, quotient rule, and power rule, is essential for mastering logarithmic conversion. By grasping these fundamental concepts, one can efficiently convert values to their logarithmic equivalents, unlocking the power of logarithms in various fields.
How to Convert to Log: A General Approach
Converting a value to its logarithmic equivalent is a straightforward process that involves understanding the logarithmic function and its properties. The general formula for logarithmic conversion is logₐ(x) = y, where x is the value, a is the base, and y is the logarithm. To convert a value to log, follow these step-by-step instructions: first, identify the base of the logarithm (e for natural logarithm or 10 for common logarithm); second, raise the base to the power of the value; and third, find the exponent that satisfies the equation. For example, to convert 100 to its natural logarithm, raise e to the power of 100 and find the exponent, which is approximately 4.605. By mastering this general approach, one can efficiently convert values to their logarithmic equivalents, unlocking the power of logarithms in various fields. Remember, learning how to convert to log is essential for simplifying complex calculations and revealing hidden patterns.
Converting to Natural Logarithm (ln)
Converting values to natural logarithms (ln) is a crucial skill in various mathematical and scientific applications. The natural logarithm, denoted by ln, has a base of Euler’s number (e), approximately 2.718. To convert a value to its natural logarithm, use the formula ln(x) = y, where x is the value and y is the natural logarithm. For example, to find the natural logarithm of 10, raise e to the power of 10 and find the exponent, which is approximately 2.303. Practice exercises, such as converting 50 to its natural logarithm or finding the natural logarithm of 0.5, can help reinforce understanding of this concept. Remember, learning how to convert to log, particularly natural logarithms, is essential for simplifying complex calculations and revealing hidden patterns in fields like physics, engineering, and computer science.
Converting to Common Logarithm (log)
Converting values to common logarithms (log) is another essential skill in various mathematical and scientific applications. The common logarithm, denoted by log, has a base of 10. To convert a value to its common logarithm, use the formula log(x) = y, where x is the value and y is the common logarithm. For example, to find the common logarithm of 100, raise 10 to the power of 100 and find the exponent, which is exactly 2. Understanding the differences between natural and common logarithms is crucial, as natural logarithms are used in more theoretical applications, while common logarithms are used in practical applications, such as calculating pH levels in chemistry or measuring the magnitude of earthquakes. Practice exercises, such as converting 25 to its common logarithm or finding the common logarithm of 0.01, can help reinforce understanding of this concept. Remember, learning how to convert to log, including common logarithms, is essential for simplifying complex calculations and revealing hidden patterns in fields like engineering, physics, and computer science.
Real-World Applications of Logarithmic Conversion
Logarithmic conversion has numerous practical applications across various fields, demonstrating its relevance and importance in real-world scenarios. In physics, logarithmic scales are used to measure the magnitude of earthquakes, allowing scientists to compare and analyze the intensity of seismic events. In biology, logarithmic conversion is used to model population growth and decay, enabling researchers to understand and predict the behavior of complex systems. In finance, logarithmic scales are used to analyze stock prices and returns, helping investors make informed decisions. Additionally, logarithmic conversion is used in computer science to optimize algorithms and improve data compression. By understanding how to convert to log, individuals can unlock the power of logarithms to simplify complex calculations, reveal hidden patterns, and drive innovation in their respective fields. For instance, in audio engineering, logarithmic conversion is used to measure sound levels, allowing engineers to optimize audio quality and reduce noise. These examples illustrate the significance of logarithmic conversion in various disciplines, highlighting its importance in driving progress and innovation.
Troubleshooting Common Conversion Errors
When learning how to convert to log, it’s essential to be aware of common mistakes that can lead to incorrect results. One common error is forgetting to adjust the base of the logarithm, leading to incorrect calculations. Another mistake is neglecting to check the units of the value being converted, which can result in inconsistent results. Additionally, failing to understand the difference between natural and common logarithms can lead to incorrect conversions. To avoid these errors, it’s crucial to carefully follow the step-by-step instructions for converting to logarithms and to double-check calculations. Furthermore, practicing with different types of values and logarithmic functions can help build confidence and accuracy. By being mindful of these common pitfalls, individuals can ensure accurate and efficient logarithmic conversions, ultimately mastering the process of how to convert to log. By taking the time to troubleshoot and correct common errors, individuals can unlock the full potential of logarithmic conversion and apply it to a wide range of real-world applications.
Mastering Logarithmic Conversion: Tips and Tricks
To efficiently convert values to logarithms, it’s essential to have a few tricks up your sleeve. One valuable tip is to use online calculators or logarithm tables to simplify the conversion process. Additionally, understanding how to convert to log using mental math shortcuts can save time and improve accuracy. For instance, memorizing common logarithmic values, such as log(10) = 1, can facilitate quick calculations. Furthermore, using logarithmic identities, such as the product rule and power rule, can simplify complex calculations and reduce errors. When working with large datasets, using software or programming languages, such as Python or R, can automate the conversion process and improve efficiency. By mastering these tips and tricks, individuals can streamline their workflow and unlock the full potential of logarithmic conversion. By learning how to convert to log efficiently, individuals can apply logarithmic conversion to a wide range of real-world applications, from data analysis to scientific modeling. With practice and patience, anyone can become proficient in logarithmic conversion and unlock its many benefits.