Understanding Bond Basics: Yield, Maturity, and Coupon
Bonds are debt securities that represent a loan made by an investor to a borrower (typically a corporation or government). Understanding the fundamental terminology associated with bonds is crucial for effectively valuing them. Key terms include yield to maturity (YTM), coupon rate, face value (par value), and maturity date. A comprehensive understanding of these terms forms the foundation for how to calculate the price of a bond in excel.
Yield to maturity (YTM) represents the total return anticipated on a bond if held until it matures. It’s essentially the internal rate of return on the investment. The coupon rate specifies the annual interest rate paid to the bondholder, expressed as a percentage of the face value. Face value, or par value, is the amount the bond will be redeemed for at maturity. The maturity date is the date on which the bond’s principal is due to be repaid. For instance, a bond with a face value of $1,000 and a coupon rate of 5% will pay $50 in interest annually. Calculating the present value of these future cash flows is fundamental to how to calculate the price of a bond in excel. The investor’s required rate of return, often represented by the yield to maturity (YTM), is crucial for accurately determining the bond’s price.
A thorough grasp of these fundamental concepts is essential for successfully applying the discounted cash flow (DCF) approach in excel, a crucial method for determining the intrinsic value of a bond. Knowing how to calculate the price of a bond in excel is vital for making informed investment decisions, especially in today’s complex financial markets. This understanding will form a strong basis for the subsequent steps in bond valuation, including the utilization of spreadsheets and specific formulas.
The Discounted Cash Flow (DCF) Approach to Bond Valuation
Bond valuation, a crucial aspect of fixed-income investments, hinges on the concept of discounted cash flow (DCF). The DCF method fundamentally values a bond by determining the present value of all future cash flows associated with it. These future cash flows consist of periodic coupon payments and the par value (face value) of the bond received at maturity. Understanding how to calculate the price of a bond in Excel using this method is a significant advantage for financial professionals.
The core principle rests on the time value of money. Future cash flows, regardless of their magnitude, are worth less today due to their deferred nature. This discounting is achieved using a discount rate, typically represented by the yield to maturity (YTM) of the bond. A higher YTM implies a greater opportunity cost of investing in the bond, resulting in a lower present value for its future cash flows. Conversely, a lower YTM signifies a smaller opportunity cost, hence a higher present value. The present value of these discounted cash flows (coupon payments and face value) is then summed to arrive at the theoretical fair market price of the bond. This approach is crucial for assessing the intrinsic value of a bond and comparing it to its market price to make informed investment decisions. The YTM directly impacts how each future cash flow is discounted, making it a vital component in understanding how to calculate the price of a bond in Excel accurately.
In essence, the DCF approach provides a structured method for determining the fair price of a bond by considering the expected future cash inflows from coupon payments and principal repayment, appropriately discounted to reflect the present value and the opportunity cost of the investment. By accurately discounting these future cash flows, investors can effectively estimate a bond’s intrinsic value and use that valuation to inform their investment decisions.
Setting up Your Excel Spreadsheet for Bond Pricing
To accurately calculate the price of a bond in Excel, a well-organized spreadsheet is essential. This section details the crucial steps for constructing your spreadsheet, ensuring all necessary data is correctly formatted and readily available for the subsequent calculations. Begin by creating columns for each key bond characteristic. This methodical approach will make subsequent calculations straightforward and prevent errors. Include columns for the coupon rate, face value, maturity date, yield to maturity (YTM), and the number of periods. Accurate data entry is paramount for achieving the precise bond price.
Converting the maturity date into the appropriate number of periods is a critical step. Determine whether the coupon payments are made annually or semi-annually. If payments are semi-annual, multiply the number of years until maturity by 2. This adjustment is vital for ensuring the accuracy of the present value calculations. Ensure that the yield to maturity (YTM) is also correctly entered, as this is the discount rate used to determine the present value of future cash flows.
For instance, if a bond matures in 10 years with semi-annual coupon payments, the number of periods would be 20 (10 years * 2). Accurate conversion of the maturity date and consideration of the payment frequency directly influence the subsequent calculations involved in determining the bond price in Excel. This initial setup step will lay the groundwork for accurate and efficient bond valuation within the spreadsheet environment. The meticulous approach to setting up the spreadsheet will be integral to the success of how to calculate the price of a bond in excel.
Calculating the Present Value of Coupon Payments in Excel
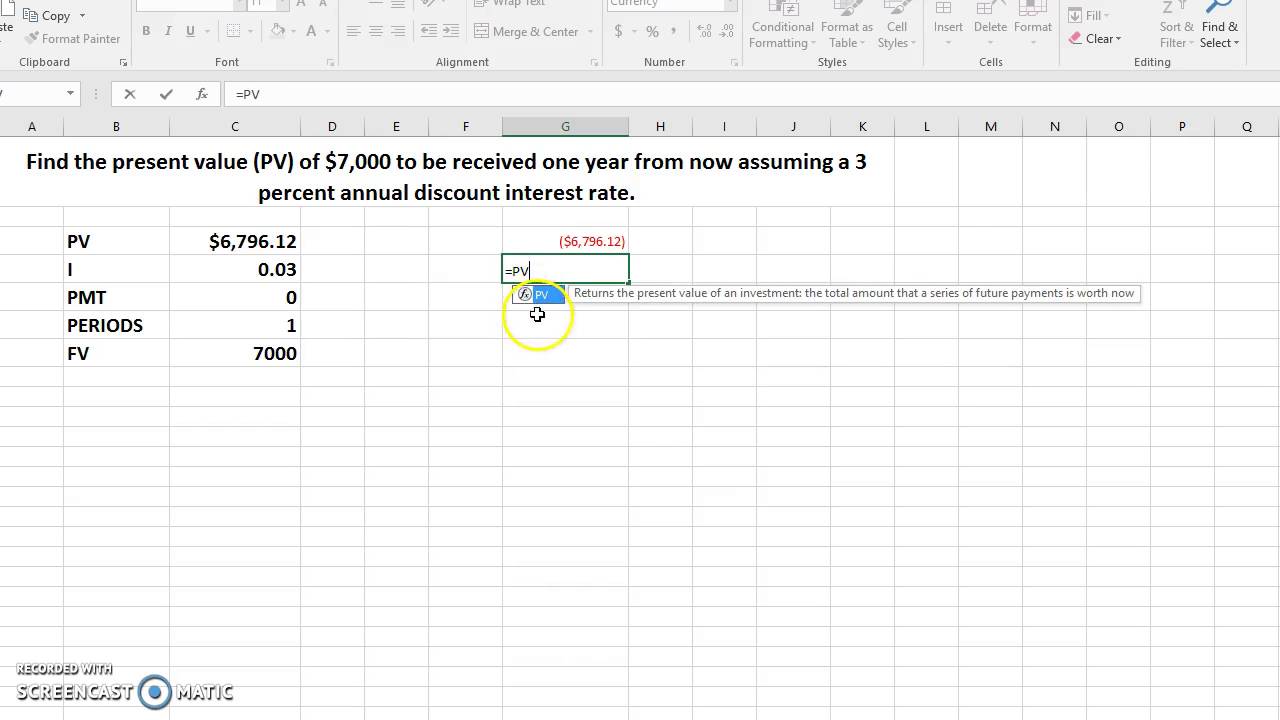
This section details how to calculate the price of a bond in excel, specifically the present value of coupon payments, using the `PV` function. The `PV` function, a cornerstone in financial modeling, allows one to determine the current worth of a series of future cash flows. For bond valuation, this translates to finding the present value of the regular coupon payments. The `PV` function requires several key arguments: `rate`, `nper`, `pmt`, and `fv`. The `rate` argument represents the discount rate per period, which is the yield to maturity (YTM) divided by the number of payment periods per year. `nper` signifies the total number of payment periods over the life of the bond. The `pmt` argument represents the coupon payment per period, calculated as the coupon rate multiplied by the face value, then divided by the number of payments per year. Finally, the `fv` (future value) argument in this case is set to 0 because we are only considering the coupon payments in this step, not the final face value payment.
For instance, consider a bond with a 5% annual coupon rate, a $1,000 face value, a 10-year maturity, and a YTM of 6%. Assuming semi-annual payments, the `rate` would be 6%/2 = 3%, `nper` would be 10*2 = 20, and `pmt` would be (5%*$1000)/2 = $25. The Excel formula in a cell to calculate the present value of coupon payments how to calculate the price of a bond in excel would be `=PV(0.03, 20, 25, 0)`. This formula calculates the present value of receiving $25 every six months for 10 years, discounted at a 3% semi-annual rate, which is a key element in how to calculate the price of a bond in excel. The result will be a negative value representing the outflow required today to receive these future coupon payments. Accurate data entry for each argument is crucial for a correct present value calculation, impacting the final bond price.
Understanding the `PV` function is essential when learning how to calculate the price of a bond in excel. By breaking down the bond’s cash flows into their respective components and applying the `PV` formula correctly, one can effectively determine the present value of the coupon payments, contributing to the overall bond valuation. Applying these steps within a well-structured spreadsheet facilitates a clear and repeatable process for bond pricing analysis. This structured approach is not only beneficial for individual bond valuation but also extends to building more complex portfolio management models in Excel, emphasizing the versatility and power of this tool for financial analysis. Remember, precise application of the `PV` function is vital for an accurate understanding of how to calculate the price of a bond in excel.
Calculating the Present Value of the Face Value in Excel
Determining the present value of the face value is a crucial step in how to calculate the price of a bond in excel. Unlike coupon payments, the face value is received only at the bond’s maturity date. The formula remains the same, the `PV` function, but the parameters differ slightly. The key difference lies in the timing of the payment—a single future payment instead of a series of periodic payments. Consequently, the `PMT` argument in the `PV` function becomes zero.
To illustrate, consider a bond with a face value of $1,000, a yield to maturity (YTM) of 5%, and a maturity of 10 years. Assume semi-annual coupon payments. In the Excel spreadsheet, the face value, maturity date, and YTM are already entered. The key is understanding how to use the appropriate values for the remaining parameters in the `PV` function. The `rate` parameter is the semi-annual yield (YTM/2), and the `nper` parameter is the total number of periods (maturity in years multiplied by the number of periods per year). The `pmt` parameter is zero, and the `fv` parameter represents the future value—the face value of the bond. This calculation determines the present value of the principal repayment.
To accurately calculate the present value of the face value in the context of how to calculate the price of a bond in excel, one must diligently enter the right data points into the correct cells. A consistent approach across various bond types is critical. Ensuring that the periodicity of coupon payments (e.g., semi-annual) aligns with the calculation of the number of periods ensures accuracy in the price determination. The `PV` function with these parameters directly yields the present value of this lump-sum payment. By incorporating this step, the spreadsheet accurately reflects the total value of the bond, comprising both the present value of the coupon payments and the present value of the face value. Consistency in data entry and understanding the function arguments is crucial for accurate bond valuation. This final present value, combined with the sum of the present values of all coupon payments, forms the total present value representing the fair price of the bond.
Summing Present Values to Determine Bond Price
To arrive at the theoretical fair price of the bond, simply sum the present values calculated in the previous two steps. This total present value represents the calculated price of the bond. Carefully review the calculations to ensure accuracy, as even minor errors in data entry can significantly affect the final result. For instance, incorrect input of the coupon rate or yield to maturity will directly impact the calculated present values. This step is crucial for understanding how to calculate the price of a bond in Excel, highlighting the relationship between inputs and outputs.
Potential discrepancies might arise from rounding errors. Excel’s handling of decimals can sometimes lead to slight variations. Therefore, if the calculated bond price does not precisely match market values, scrutinize the input data, particularly the yield to maturity and the coupon rate, for potential inaccuracies. Double-checking input data is essential for precise calculations. This attention to detail is vital for obtaining an accurate valuation of the bond. Ensuring accuracy is paramount for a comprehensive bond valuation in Excel.
Consistency in data formatting, like using the same decimal places for coupon rates and yield to maturity, can also contribute to a higher degree of precision and prevent potential errors. This rigorous approach helps eliminate any potential discrepancies that could lead to misinterpretations. Maintaining consistency in the Excel spreadsheet enhances the reliability of the bond valuation results and improves accuracy when calculating the price of a bond in excel.
Handling Different Payment Frequencies: Annual vs. Semi-annual
Most corporate bonds pay coupons semi-annually, meaning interest payments are made twice a year. Understanding how to adjust calculations for this is crucial when learning how to calculate the price of a bond in excel. For annual payments, the process is straightforward, using the bond’s stated annual coupon rate and maturity in years directly within the PV function. However, for semi-annual bonds, adjustments are necessary to accurately reflect the more frequent payments. To calculate the price of a bond in excel with semi-annual payments, the annual coupon rate must be divided by two to find the semi-annual coupon payment. Similarly, the number of periods (nper) should be doubled, representing the total number of semi-annual periods until maturity. The yield to maturity (YTM) also needs to be adjusted by dividing the annual YTM by two to reflect the semi-annual discount rate. This ensures that each cash flow is discounted to its correct present value using the appropriate semi-annual discount rate. Failing to make these adjustments will lead to inaccurate bond pricing. For example, a bond with a 6% annual coupon rate and a 10-year maturity would have a semi-annual coupon rate of 3% (6%/2) and 20 periods (10 years * 2). The annual YTM would also need to be adjusted accordingly to calculate the correct price of a bond in excel.
The Excel PV function directly facilitates this adjustment. The `rate` argument will accept the semi-annual rate, and `nper` will reflect the number of semi-annual periods. The `pmt` argument will utilize the semi-annual coupon payment. This allows for seamless calculations regardless of payment frequency. In essence, the underlying principle of present value remains consistent—discounting all future cash flows to their present value using the appropriate discount rate. The key is to ensure that the rate and the number of periods are consistently aligned with the payment frequency. This consistency is particularly important when comparing bonds with different payment frequencies or when conducting sensitivity analysis on bond prices with variations in payment structures. Knowing how to calculate the price of a bond in excel accurately across diverse scenarios is a hallmark of sophisticated financial modeling.
Consider a bond with a 5% annual coupon rate, a $1000 face value, and a 5-year maturity. For annual payments, the calculation would use a 5% rate, 5 periods, and a $50 payment. In contrast, a semi-annual equivalent would employ a 2.5% rate, 10 periods, and a $25 payment. The resulting present values, while reflecting different payment structures, will converge to a consistent bond price if the YTM is appropriately adjusted. Therefore, mastering these adjustments is critical for accurately determining the fair value of a bond regardless of the payment schedule, and therefore crucial when learning how to calculate the price of a bond in excel.
Practical Application and Scenario Analysis: Mastering How to Calculate the Price of a Bond in Excel
To solidify understanding of how to calculate the price of a bond in Excel, consider several illustrative scenarios. First, examine a bond with a face value of $1,000, a coupon rate of 5% (paid semi-annually), a maturity of 10 years, and a yield to maturity (YTM) of 6%. Using the previously described Excel methodology, one would input these values into the spreadsheet, calculating the present value of the semi-annual coupon payments and the present value of the face value at maturity. The sum of these present values yields the bond’s price. Note that because the YTM (6%) exceeds the coupon rate (5%), the bond will trade at a discount to its face value. This demonstrates how to calculate the price of a bond in Excel when the YTM is higher than the coupon rate.
Next, let’s explore a scenario where the YTM is lower than the coupon rate. Maintain the same face value ($1,000) and maturity (10 years), but change the coupon rate to 7% (semi-annual payments) and the YTM to 6%. By applying the same Excel calculations as before, one will observe that the bond price is now higher than its face value, trading at a premium. This example showcases how to calculate the price of a bond in Excel when the YTM is lower than the coupon rate. By comparing the results from these two scenarios, readers will see the inverse relationship between YTM and bond price – a fundamental principle in bond valuation. This comparative analysis provides a clear understanding of how changing market interest rates impact bond values. Understanding how to calculate the price of a bond in Excel is crucial for effective portfolio management.
Finally, to further enhance understanding of how to calculate the price of a bond in Excel and its sensitivity to different variables, explore scenarios with varying maturities. For instance, analyze the same bond with a 5% coupon rate and 6% YTM, but alter the maturity to 5 years and then 15 years. Observe how the bond price changes with shorter and longer maturities. Shorter maturities will generally lead to smaller differences between the present values of the coupon payments and face value, while longer maturities amplify these differences. This exercise highlights the impact of time on bond valuation, providing a more comprehensive understanding of the dynamics involved in determining bond prices using Excel. This thorough analysis of different scenarios using Excel will enhance proficiency in how to calculate the price of a bond in Excel, a critical skill for financial professionals and serious investors.