Understanding the Concept of Minimum Variance Portfolio
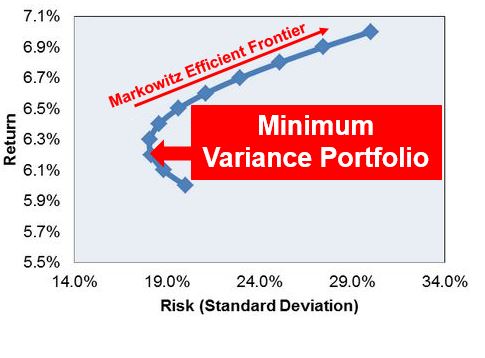
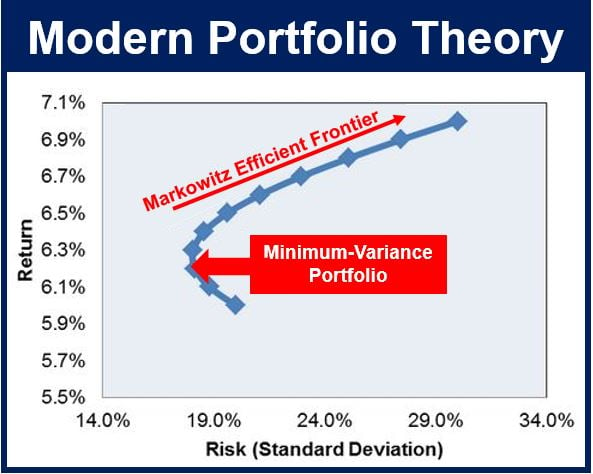
In the world of investment management, risk management is a crucial aspect of achieving financial goals. One effective strategy to minimize risk is by constructing a portfolio that minimizes the overall risk or volatility, while maximizing potential returns. This approach is known as the minimum variance portfolio. By understanding how to calculate the minimum variance portfolio, investors can create a diversified portfolio that balances risk and return, ultimately achieving their financial objectives. The concept of minimum variance portfolio is based on the idea that investors can reduce their exposure to market fluctuations by diversifying their investments. By doing so, investors can minimize the risk of losses and maximize potential gains. In essence, a minimum variance portfolio is a portfolio that is optimized to reduce risk, making it an attractive option for investors seeking to balance risk and return.
The Benefits of Diversification in Portfolio Construction
Diversification is a fundamental concept in portfolio construction, and it plays a crucial role in minimizing risk and maximizing returns. By spreading investments across different asset classes, sectors, and geographic regions, investors can reduce their exposure to market fluctuations and increase the potential for long-term growth. A diversified portfolio can help to mitigate risk by reducing the impact of any one investment on the overall portfolio. This, in turn, can lead to more stable returns and a lower risk profile. Furthermore, diversification can also increase potential returns by allowing investors to take advantage of opportunities in different markets and sectors. By understanding how to calculate the minimum variance portfolio, investors can create a diversified portfolio that balances risk and return, ultimately achieving their financial objectives. Effective diversification can also improve overall portfolio performance by reducing volatility and increasing the potential for long-term growth.
How to Calculate Minimum Variance Portfolio: A Step-by-Step Approach
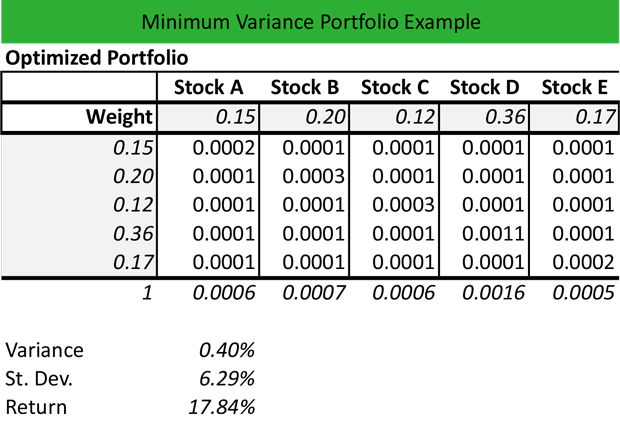
Calculating the minimum variance portfolio is a crucial step in portfolio risk management. To do so, investors need to follow a step-by-step approach that involves several key steps. First, investors need to gather historical data on the returns of the assets they wish to include in their portfolio. This data should be collected over a sufficient period to provide a reliable estimate of the assets’ risk profiles. Next, investors need to calculate the covariance matrix of the assets, which measures the degree of correlation between each pair of assets. This matrix is essential in determining the overall risk of the portfolio. Once the covariance matrix is calculated, investors can use optimization techniques, such as mean-variance optimization or Black-Litterman model, to determine the optimal portfolio weights that minimize the portfolio’s variance. Finally, investors need to monitor and adjust their portfolio regularly to ensure that it remains aligned with their investment objectives and risk tolerance. By following these steps, investors can learn how to calculate the minimum variance portfolio and create a diversified portfolio that balances risk and return. Understanding how to calculate the minimum variance portfolio is essential in achieving investment success, as it allows investors to make informed decisions about their investments and optimize their returns while minimizing risk.
The Role of Covariance in Portfolio Risk Management
Covariance is a crucial concept in portfolio risk management, as it measures the degree of correlation between different assets in a portfolio. In essence, covariance captures the tendency of two or more assets to move together in response to changes in the market. A high covariance between two assets means that they tend to move in the same direction, while a low covariance indicates that they tend to move independently. Understanding covariance is essential in calculating the minimum variance portfolio, as it allows investors to identify the optimal portfolio weights that minimize risk. By incorporating covariance into the portfolio construction process, investors can create a diversified portfolio that balances risk and return. For instance, if two assets have a high covariance, it may be wise to reduce the weight of one of the assets to minimize the overall risk of the portfolio. On the other hand, if two assets have a low covariance, it may be beneficial to increase the weight of one of the assets to take advantage of potential returns. By understanding how to calculate the minimum variance portfolio and incorporating covariance into the portfolio construction process, investors can make informed decisions about their investments and optimize their returns while minimizing risk.
Using Historical Data to Estimate Portfolio Risk
Estimating portfolio risk is a critical step in calculating the minimum variance portfolio. One of the most effective ways to do this is by using historical data. Historical data provides a wealth of information about the past behavior of different assets, including their returns, volatility, and correlations. By analyzing this data, investors can gain valuable insights into the potential risks and returns of their portfolio. To use historical data effectively, investors should collect a sufficient amount of data, typically several years’ worth, and analyze it using statistical techniques such as mean-variance analysis or Monte Carlo simulations. This analysis can help investors identify the optimal portfolio weights that minimize risk and maximize returns. Additionally, historical data can be used to estimate the covariance matrix, which is a critical input in calculating the minimum variance portfolio. By incorporating historical data into the portfolio construction process, investors can make more informed decisions about their investments and optimize their returns while minimizing risk. Furthermore, using historical data can also help investors to identify potential pitfalls and avoid common mistakes when calculating the minimum variance portfolio. By understanding how to use historical data effectively, investors can create a robust and diversified portfolio that achieves their investment objectives.
Common Pitfalls to Avoid When Calculating Minimum Variance Portfolio
When calculating the minimum variance portfolio, investors should be aware of common pitfalls that can lead to suboptimal portfolio construction. One of the most common mistakes is errors in data collection, which can result in inaccurate estimates of asset returns and covariance. This can lead to a portfolio that is not truly optimized for minimum risk. Another pitfall is making incorrect assumptions about the behavior of assets, such as assuming that historical returns will continue into the future. This can result in a portfolio that is not robust to changing market conditions. Inadequate risk management is also a common pitfall, as investors may fail to account for potential risks such as liquidity risk or credit risk. Additionally, investors may also overlook the importance of regular portfolio rebalancing, which can lead to a portfolio that drifts away from its optimal weights. Furthermore, investors should also be cautious of over-reliance on a single optimization technique, such as mean-variance optimization, and should consider using multiple approaches to ensure a robust portfolio. By being aware of these common pitfalls, investors can avoid common mistakes and ensure that their minimum variance portfolio is truly optimized for minimum risk and maximum returns. It is essential to understand how to calculate the minimum variance portfolio correctly to avoid these pitfalls and achieve investment objectives.
Real-World Applications of Minimum Variance Portfolio in Investment Management
The minimum variance portfolio has been widely adopted in investment management due to its ability to optimize investment returns while minimizing risk. One notable example is the Norwegian Government Pension Fund, which uses a minimum variance approach to manage its $1 trillion portfolio. By doing so, the fund has been able to reduce its risk exposure while maintaining its returns. Another example is the investment management firm, BlackRock, which offers a range of minimum variance portfolios to its clients. These portfolios have been designed to provide investors with a more stable source of returns, while also reducing their exposure to market volatility. In addition, many institutional investors, such as pension funds and endowments, have also incorporated minimum variance portfolios into their investment strategies. By understanding how to calculate the minimum variance portfolio, investors can create a robust and diversified portfolio that achieves their investment objectives. For instance, a study by the CFA Institute found that minimum variance portfolios outperformed traditional market-capitalization-weighted portfolios during times of market stress. These real-world applications demonstrate the effectiveness of the minimum variance portfolio in investment management and highlight its potential to optimize investment returns while minimizing risk.
Conclusion: Optimizing Your Investment Strategy with Minimum Variance Portfolio
In conclusion, the minimum variance portfolio is a powerful tool for investors seeking to optimize their investment returns while minimizing risk. By understanding how to calculate the minimum variance portfolio, investors can create a robust and diversified portfolio that achieves their investment objectives. The importance of minimum variance portfolio in investment strategy cannot be overstated, as it provides a framework for investors to manage risk and maximize returns. By avoiding common pitfalls and incorporating real-world applications of minimum variance portfolio, investors can create a portfolio that is tailored to their unique needs and goals. Ultimately, the key to optimizing investment returns while minimizing risk is to understand how to calculate the minimum variance portfolio and to incorporate it into a comprehensive investment strategy. By doing so, investors can achieve their financial goals and secure their financial future.