Understanding the Concept of Average Return in Investing
In the world of investing, making informed decisions is crucial to achieving financial goals. One essential metric that helps investors evaluate the performance of their investments is the average return. The average return provides a snapshot of an investment’s historical performance, enabling investors to assess its potential for future growth. In this article, we will delve into the concept of average return, its importance in investment analysis, and how it helps investors make informed decisions.
The average return is a critical component of investment analysis, as it helps investors understand the overall performance of their investments over a specific period. By calculating the average return, investors can determine whether their investments are meeting their expected returns, identify areas for improvement, and make adjustments to their investment strategies. Moreover, the average return is a key metric used to compare the performance of different investments, such as mutual funds, stocks, and bonds.
When it comes to calculating the average return, investors have two primary options: arithmetic average return and geometric average return. While both methods have their advantages and disadvantages, the arithmetic average return is a more straightforward and widely used approach. In the following sections, we will explore the arithmetic average return in more detail, including its formula, calculation, and interpretation.
By grasping the concept of average return and learning how to calculate the arithmetic average return, investors can gain valuable insights into their investments’ performance. This knowledge enables investors to make more informed decisions, optimize their investment portfolios, and ultimately achieve their financial objectives.
What is Arithmetic Average Return and Why Does it Matter?
The arithmetic average return is a widely used metric in investment analysis that helps investors understand the performance of their investments over a specific period. It is calculated by adding up the returns for each period and dividing the result by the number of periods. The formula for arithmetic average return is:
Ra = (R1 + R2 + … + Rn) / n
where Ra is the arithmetic average return, R1, R2, …, Rn are the returns for each period, and n is the number of periods.
The arithmetic average return is important because it provides a simple and intuitive way to understand the average performance of an investment. It is particularly useful for investments with a short to medium-term horizon, as it helps investors evaluate the investment’s potential for growth and income generation.
In contrast to the geometric average return, which takes into account the compounding effect of returns, the arithmetic average return does not account for compounding. This means that the arithmetic average return will always be higher than the geometric average return, especially for investments with a longer time horizon. Despite this limitation, the arithmetic average return remains a popular metric among investors due to its simplicity and ease of calculation.
Understanding the arithmetic average return is crucial for investors who want to make informed decisions about their investments. By learning how to calculate the arithmetic average return, investors can gain valuable insights into their investments’ performance and make adjustments to their investment strategies accordingly. In the next section, we will provide a step-by-step guide on how to calculate the arithmetic average return, including an example to illustrate the calculation.
How to Calculate Arithmetic Average Return: A Simple Formula
Calculating the arithmetic average return is a straightforward process that involves adding up the returns for each period and dividing the result by the number of periods. Here’s a step-by-step guide on how to calculate the arithmetic average return:
Step 1: Gather the returns for each period. This can be done by collecting the historical data on the investment’s performance, such as the returns for each year or quarter.
Step 2: Add up the returns for each period. This can be done using a simple addition formula, such as:
R1 + R2 + … + Rn
where R1, R2, …, Rn are the returns for each period.
Step 3: Divide the result by the number of periods. This can be done using a simple division formula, such as:
(R1 + R2 + … + Rn) / n
where n is the number of periods.
For example, let’s say we want to calculate the arithmetic average return for an investment that has returned 10%, 15%, and 20% over the past three years. Using the formula above, we would calculate the arithmetic average return as follows:
(10% + 15% + 20%) / 3 = 15%
Therefore, the arithmetic average return for this investment is 15%.
By following these simple steps, investors can easily calculate the arithmetic average return for their investments and gain valuable insights into their performance. Remember, understanding how to calculate the arithmetic average return is crucial for making informed investment decisions. In the next section, we will discuss how to interpret the results of the arithmetic average return calculation.
Interpreting Arithmetic Average Return: What Does it Tell You?
Once you have calculated the arithmetic average return, it’s essential to understand what it reveals about the investment’s performance and potential risks. The arithmetic average return provides a snapshot of the investment’s historical performance, helping investors to:
Evaluate investment performance: The arithmetic average return gives investors an idea of how well their investment has performed over a specific period. A higher arithmetic average return indicates better performance, while a lower return may suggest underperformance.
Assess risk: The arithmetic average return can also provide insights into the investment’s risk profile. A higher arithmetic average return may indicate higher volatility, while a lower return may suggest a more stable investment.
Compare investments: The arithmetic average return enables investors to compare the performance of different investments, such as mutual funds or stocks. This helps investors to make informed decisions about which investments to hold or sell.
Set expectations: The arithmetic average return can help investors set realistic expectations for future performance. By understanding the historical performance of an investment, investors can better anticipate its potential for growth or income generation.
Identify trends: The arithmetic average return can also help investors identify trends in the investment’s performance. For example, a declining arithmetic average return may indicate a downward trend, while an increasing return may suggest an upward trend.
By interpreting the arithmetic average return correctly, investors can gain valuable insights into their investments and make more informed decisions. In the next section, we will discuss common pitfalls to avoid when calculating the arithmetic average return.
Common Pitfalls to Avoid When Calculating Arithmetic Average Return
When calculating the arithmetic average return, it’s essential to avoid common mistakes that can lead to inaccurate results. Here are some common pitfalls to watch out for:
Ignoring Compounding: One of the most significant mistakes investors make is ignoring compounding when calculating the arithmetic average return. Compounding can significantly impact the investment’s performance, and failing to account for it can lead to inaccurate results.
Using Incorrect Data: Using incorrect or outdated data can lead to inaccurate calculations. Ensure that you are using the correct data, and that it is up-to-date and relevant to the investment.
Failing to Account for Fees: Fees and expenses can eat into the investment’s returns, and failing to account for them can lead to inaccurate calculations. Make sure to include all fees and expenses when calculating the arithmetic average return.
Not Considering the Time Period: The time period used to calculate the arithmetic average return can significantly impact the results. Ensure that you are using a relevant time period that accurately reflects the investment’s performance.
Not Adjusting for Inflation: Inflation can erode the investment’s returns, and failing to adjust for it can lead to inaccurate calculations. Make sure to adjust for inflation when calculating the arithmetic average return.
By avoiding these common pitfalls, investors can ensure that their calculations are accurate and reliable. In the next section, we will explore real-world applications of arithmetic average return in investing.
Real-World Applications of Arithmetic Average Return in Investing
The arithmetic average return has numerous real-world applications in investing, helping investors to make informed decisions and evaluate investment performance. Here are some examples:
Evaluating Mutual Fund Performance: The arithmetic average return is commonly used to evaluate the performance of mutual funds. By calculating the arithmetic average return of a mutual fund, investors can compare its performance to that of other funds and make informed investment decisions.
Comparing Investment Portfolios: The arithmetic average return can be used to compare the performance of different investment portfolios. This helps investors to identify which portfolios are performing well and which ones need adjustments.
Assessing Risk: The arithmetic average return can also be used to assess the risk associated with an investment. A higher arithmetic average return may indicate higher volatility, while a lower return may suggest a more stable investment.
Setting Investment Goals: The arithmetic average return can be used to set realistic investment goals. By understanding the historical performance of an investment, investors can set achievable goals and develop a strategy to achieve them.
Measuring Performance Against Benchmarks: The arithmetic average return can be used to measure the performance of an investment against benchmarks, such as the S&P 500. This helps investors to evaluate the performance of their investments and make adjustments as needed.
In addition to these examples, the arithmetic average return has many other real-world applications in investing. By understanding how to calculate and interpret the arithmetic average return, investors can make more informed decisions and achieve their investment goals.
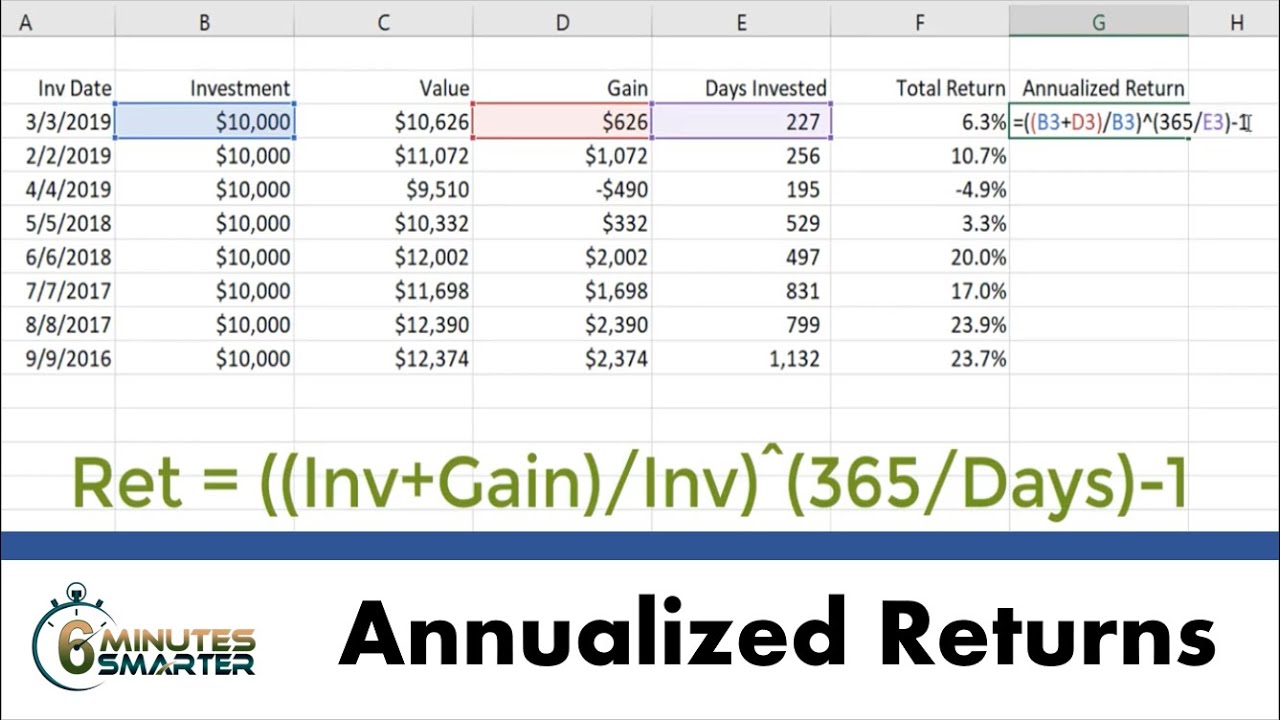
Calculating Arithmetic Average Return in Excel: A Practical Guide
Microsoft Excel is a powerful tool that can be used to calculate the arithmetic average return with ease. Here’s a step-by-step guide on how to calculate the arithmetic average return in Excel:
Step 1: Enter the Data
Enter the investment returns data into a column in Excel, with each return value in a separate cell. For example, if you have 5 years of returns data, enter the returns for each year in cells A1 to A5.
Step 2: Calculate the Arithmetic Average Return
To calculate the arithmetic average return, use the AVERAGE function in Excel. The formula is:
=AVERAGE(range)
Where “range” is the range of cells containing the returns data. For example, if the returns data is in cells A1 to A5, the formula would be:
=AVERAGE(A1:A5)
Step 3: Interpret the Results
The result of the formula will be the arithmetic average return. This value represents the average return of the investment over the specified period.
Tips and Variations:
– To calculate the arithmetic average return for a specific period, simply adjust the range of cells in the formula.
– To calculate the arithmetic average return for multiple investments, use the AVERAGE function for each investment and compare the results.
– To calculate the arithmetic average return with compounding, use the XNPV function in Excel, which takes into account the compounding effect.
By following these steps, investors can easily calculate the arithmetic average return in Excel and gain valuable insights into their investment performance. Remember to always use accurate and up-to-date data to ensure reliable results.
Conclusion: Mastering Arithmetic Average Return for Informed Investment Decisions
In conclusion, understanding how to calculate the arithmetic average return is a crucial skill for investors seeking to make informed decisions. By grasping the concept of arithmetic average return, investors can gain valuable insights into investment performance, identify potential risks, and make data-driven decisions.
Throughout this guide, we have covered the importance of arithmetic average return, its formula, and how to calculate it using a simple step-by-step process. We have also explored how to interpret the results, common pitfalls to avoid, and real-world applications of arithmetic average return in investing.
Moreover, we have provided a practical guide on how to calculate arithmetic average return in Microsoft Excel, making it easier for investors to apply this concept in their investment analysis.
By mastering the arithmetic average return, investors can unlock valuable insights into their investments and make more informed decisions. Whether evaluating mutual fund performance, comparing investment portfolios, or assessing risk, the arithmetic average return is a powerful tool that can help investors achieve their investment goals.
Remember, understanding how to calculate the arithmetic average return is just the first step. The key to success lies in applying this knowledge in real-world investment scenarios and continually refining your investment strategy to achieve optimal results.