How to Calculate Option Price

Understanding the Basics of Options Trading

In the world of finance, options trading has become an increasingly popular investment strategy. But what exactly are options, and how do they work? In essence, an option is a contract that gives the buyer the right, but not the obligation, to buy or sell an underlying asset at a predetermined price on or before a certain date. This flexibility makes options an attractive tool for investors seeking to manage risk, speculate on price movements, or generate income.

Options trading offers several benefits, including the potential for higher returns, risk management, and flexibility. By incorporating options into an investment strategy, investors can hedge against potential losses, speculate on price movements, or generate income through the sale of options. To fully leverage these benefits, it’s essential to understand the intricacies of options trading, including how to calculate option prices accurately. In fact, learning how to calculate option price is a crucial step in developing a successful options trading strategy.

The Role of Pricing in Options Trading

In options trading, accurate pricing is crucial for making informed investment decisions. Mispricing can lead to significant losses, making it essential to understand the importance of reliable pricing models. A pricing model that accurately reflects the value of an option can help investors identify profitable opportunities, manage risk, and optimize their investment strategies.

The consequences of mispricing can be severe. Overvaluing an option can result in buying at an inflated price, while undervaluing can lead to selling at a lower price than its true worth. In both cases, investors may incur significant losses. Therefore, it’s essential to understand how to calculate option price using a reliable pricing model, such as the Black-Scholes model, to make informed investment decisions.

A reliable pricing model takes into account various factors that influence option prices, including underlying stock price, volatility, time to expiration, and interest rates. By understanding these factors and how they interact, investors can develop a more accurate pricing model, enabling them to make more informed investment decisions. In the next section, we’ll delve deeper into the Black-Scholes model, a widely used option pricing formula, and explore its assumptions, limitations, and applications.

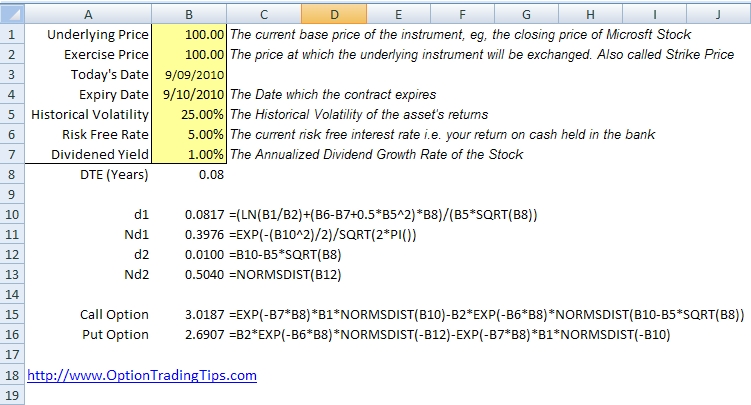
How to Calculate Option Price: The Black-Scholes Model

The Black-Scholes model is a widely used option pricing formula that provides a framework for calculating the value of a call or put option. Developed by Fischer Black and Myron Scholes in 1973, this model is based on several assumptions, including the idea that the underlying stock price follows a geometric Brownian motion, that there are no transaction costs or dividends, and that the risk-free interest rate is constant.

The Black-Scholes model takes into account five key factors that influence option prices: the underlying stock price, the strike price, the time to expiration, the risk-free interest rate, and the volatility of the underlying stock. By incorporating these factors, the model provides a reliable estimate of an option’s value, enabling investors to make informed investment decisions. To learn how to calculate option price using the Black-Scholes model, investors can use online calculators or financial software that implement this formula.

While the Black-Scholes model is a powerful tool for option pricing, it has several limitations. For example, it assumes that the underlying stock price follows a lognormal distribution, which may not always be the case. Additionally, the model does not account for dividends or transaction costs, which can affect option prices. Despite these limitations, the Black-Scholes model remains a widely used and influential option pricing formula, providing a foundation for more advanced models and techniques.

Key Factors Affecting Option Price

When learning how to calculate option price, it’s essential to understand the key factors that influence option prices. These factors interact with each other in complex ways, making it crucial to consider them all when making investment decisions. The following factors are the most significant determinants of option prices:

The underlying stock price is perhaps the most obvious factor affecting option prices. As the stock price increases, the value of call options also increases, while the value of put options decreases. Conversely, a decrease in the stock price leads to a decrease in call option value and an increase in put option value.

Volatility is another critical factor in option pricing. Options on highly volatile stocks are more valuable than those on less volatile stocks, as there is a greater likelihood of significant price movements. Time to expiration is also important, as options with longer expirations are generally more valuable than those with shorter expirations.

Interest rates also play a role in option pricing, as they affect the cost of carrying a position. Higher interest rates increase the cost of carrying a position, which can lead to lower option prices. Finally, dividends can also impact option prices, as they reduce the value of the underlying stock and, consequently, the value of call options.

Understanding these key factors is crucial for accurate option pricing. By considering the interactions between these factors, investors can develop a more nuanced understanding of how to calculate option price and make more informed investment decisions.

Using Greeks to Refine Option Pricing

In options trading, understanding the Greeks is essential for refining option pricing and making informed investment decisions. The Greeks – delta, gamma, theta, and vega – are metrics that measure the sensitivity of an option’s price to changes in various underlying factors. By grasping the Greeks, investors can better understand how to calculate option price and adjust their strategies accordingly.

Delta, the most widely used Greek, measures the rate of change of an option’s price with respect to the underlying stock price. Call options have positive delta, while put options have negative delta. Gamma, on the other hand, measures the rate of change of delta, providing insight into the volatility of an option’s price.

Theta, also known as time decay, measures the rate of change of an option’s price with respect to time. As time passes, the value of an option decreases, making theta a critical factor in option pricing. Vega, the final Greek, measures the rate of change of an option’s price with respect to volatility. Options with higher vega are more sensitive to changes in volatility.

By understanding the Greeks, investors can refine their option pricing strategies and make more informed decisions. For example, an investor seeking to hedge against potential losses might focus on options with high delta and gamma, while an investor seeking to capitalize on volatility might focus on options with high vega. By incorporating the Greeks into their analysis, investors can develop a more nuanced understanding of how to calculate option price and optimize their investment strategies.

Real-World Examples of Option Pricing in Action

To illustrate the practical application of option pricing models, let’s consider a few real-world examples. These examples will demonstrate how to calculate option price in different scenarios, highlighting the importance of accurate pricing in options trading.

Example 1: Google Stock Options

In 2017, Google’s stock price was trading around $900. An investor wanted to buy a call option with a strike price of $920, expiring in three months. Using the Black-Scholes model, the option price was calculated to be $23.50. This example illustrates how to calculate option price using a widely used pricing model, taking into account factors such as underlying stock price, volatility, and time to expiration.

Example 2: Apple Stock Options

In 2019, Apple’s stock price was trading around $200. An investor wanted to sell a put option with a strike price of $190, expiring in six months. Using a binomial model, the option price was calculated to be $12.25. This example demonstrates the application of an advanced option pricing technique, highlighting the importance of considering multiple factors when calculating option prices.

These examples illustrate how option pricing models are used in real-world scenarios to calculate option prices. By understanding how to apply these models, investors can make more informed decisions and optimize their investment strategies. Whether using the Black-Scholes model or more advanced techniques, accurate option pricing is crucial for success in options trading.

Common Pitfalls to Avoid in Option Pricing

When it comes to calculating option prices, even small mistakes can have significant consequences. To avoid costly errors, it’s essential to be aware of common pitfalls that can lead to inaccurate option pricing. By understanding these mistakes, investors can refine their approach to how to calculate option price and make more informed investment decisions.

One common mistake is ignoring volatility skew, which can lead to mispricing of options. Volatility skew refers to the difference in implied volatility between options with different strike prices. Failing to account for this phenomenon can result in inaccurate option prices and poor investment decisions.

Another pitfall is neglecting to consider dividends when calculating option prices. Dividends can significantly impact the underlying stock price, and failing to account for them can lead to inaccurate option pricing. Investors must incorporate dividend payments into their option pricing models to ensure accurate results.

Additionally, investors should avoid using simplistic models that fail to account for complex market dynamics. The Black-Scholes model, for example, assumes a constant volatility and interest rate, which may not reflect real-world market conditions. More advanced models, such as binomial models or Monte Carlo simulations, can provide a more accurate picture of option prices.

Finally, investors should be cautious of relying too heavily on historical data when calculating option prices. While historical data can provide valuable insights, it may not accurately reflect future market conditions. Investors must be aware of the limitations of historical data and incorporate other factors, such as market sentiment and economic indicators, into their option pricing models.

By avoiding these common pitfalls, investors can develop a more accurate and effective approach to how to calculate option price, ultimately leading to better investment decisions and improved portfolio performance.

Advanced Option Pricing Techniques and Models

For readers seeking more sophisticated approaches to option pricing, there are several advanced techniques and models that can provide a more accurate and nuanced understanding of how to calculate option price. These models can help investors better navigate complex market conditions and make more informed investment decisions.

One such approach is the binomial model, which uses a lattice-based framework to estimate option prices. This model is particularly useful for pricing American-style options, which can be exercised at any time before expiration. By breaking down the option’s lifetime into discrete time periods, the binomial model can provide a more accurate estimate of option prices.

Another advanced technique is the finite difference method, which uses numerical methods to solve partial differential equations that describe option prices. This approach is particularly useful for pricing options with complex payoff structures or those that are sensitive to changes in underlying asset prices.

Monte Carlo simulations are another advanced technique used to calculate option prices. These simulations involve generating multiple scenarios of possible outcomes and estimating the option’s value based on these scenarios. This approach is particularly useful for pricing options with multiple underlying assets or those that are sensitive to changes in volatility.

In addition to these models, there are also several other advanced techniques that can be used to refine option pricing, such as the Fourier transform method and the trinomial model. These models can provide a more accurate and nuanced understanding of how to calculate option price, ultimately leading to better investment decisions and improved portfolio performance.

By incorporating these advanced techniques and models into their approach to option pricing, investors can gain a more sophisticated understanding of the complex factors that influence option prices. Whether using the Black-Scholes model or more advanced approaches, understanding how to calculate option price is crucial for success in options trading.