Understanding Volatility: A Foundation for Investment Success
Volatility measures the extent of price fluctuations in financial markets. Understanding volatility is crucial for investors, as it directly impacts investment returns. High volatility implies significant price swings, leading to potentially larger profits or losses. Conversely, low volatility suggests more stable prices and less dramatic returns. Learning how to calculate historical volatility empowers investors to assess risk and make better-informed decisions. Historical volatility, a key metric, analyzes past price movements to predict future price behavior. This guide will equip you with the knowledge and skills to effectively measure and interpret volatility. Mastering this skill is fundamental to managing investment risk effectively. The ability to predict and measure volatility will improve your portfolio management capabilities. This understanding helps you make more calculated investment choices.
Price fluctuations, the essence of volatility, reflect market sentiment, economic events, and company-specific news. These fluctuations create uncertainty and risk. Investors seeking high returns often accept higher volatility. Conversely, risk-averse investors prefer lower volatility assets, even if it means sacrificing potential returns. The ability to accurately assess and manage risk through volatility analysis is a critical skill for any investor, regardless of experience level. Understanding how to calculate historical volatility is the first step towards navigating these complexities and making profitable investment choices. It lays the groundwork for advanced risk management and investment strategies.
Before exploring how to calculate historical volatility, it’s important to grasp its implications. High volatility presents opportunities for significant gains, but also for substantial losses. Low volatility offers more stability but potentially lower returns. Understanding these trade-offs enables the creation of a well-diversified portfolio tailored to individual risk tolerance and investment goals. This guide will provide the necessary tools and techniques to assess volatility accurately and apply this knowledge to practical investment scenarios. By learning how to calculate historical volatility, investors can refine their investment approach and increase the likelihood of success. This crucial skill empowers investors to navigate the challenges and opportunities of the financial markets with confidence and skill.
Choosing Your Data: The Cornerstone of Accurate Calculations
Selecting reliable and appropriate price data is crucial for accurately calculating historical volatility. The accuracy of your volatility calculation directly depends on the quality of your input data. Various sources provide financial data, including Yahoo Finance and Bloomberg. Each source may have slightly different data, and understanding these differences is important for consistency. Choosing between daily, weekly, or monthly data impacts the volatility calculation. Daily data provides more granular information, potentially capturing short-term fluctuations, while monthly data reveals longer-term trends. The frequency of the data directly influences the final volatility number; higher frequency data often shows higher volatility. To understand how to calculate historical volatility accurately, using adjusted closing prices is paramount. Adjusted prices account for corporate actions like stock splits and dividends, providing a consistent and comparable price series, free from distortions caused by these events. This ensures that the volatility calculation reflects only actual price changes, not artificial ones resulting from corporate actions. Understanding how these choices affect the calculation is vital for learning how to calculate historical volatility effectively.
Different data sources may offer various pricing adjustments. Some sources might adjust for dividends only, while others might also incorporate adjustments for stock splits and other corporate actions. The choice of data source will depend on the specific needs of the analysis and the availability of data. For example, if analyzing long-term trends, monthly data may suffice, while studying short-term market reactions might necessitate daily data. Remember, choosing the right data frequency is crucial for interpreting results accurately. If you are trying to learn how to calculate historical volatility, understanding your chosen data is extremely important. The consistency and accuracy of your data directly translate to the quality and usefulness of your volatility calculation. Inaccurate or incomplete data leads to misleading results, hindering the effective assessment of risk.
Furthermore, the choice of data also impacts the interpretation of the final volatility value. Daily data, for example, will generally show higher volatility compared to monthly data for the same asset. This is because daily data captures more frequent price fluctuations. This emphasizes the importance of selecting a data frequency that aligns with the investment horizon and the specific question being addressed. Always ensure the data used in how to calculate historical volatility is appropriately adjusted to avoid errors in the analysis. Careful consideration of data sources and frequency is an essential element of successfully calculating historical volatility and deriving meaningful insights. Understanding these nuances is integral to the accuracy and reliability of the results in your calculation of historical volatility.
Calculating Log Returns: A Crucial Intermediate Step in How to Calculate Historical Volatility
When learning how to calculate historical volatility, understanding log returns is essential. Simple returns, calculated as (Pt – Pt-1) / Pt-1, where Pt is the price at time t and Pt-1 is the price at time t-1, have limitations. Specifically, they are not additive over time, making long-term statistical analysis challenging. Log returns, however, address this limitation. They are calculated as ln(Pt / Pt-1), where ‘ln’ denotes the natural logarithm. This method provides a more accurate representation of percentage changes, especially for larger price movements. The additivity property of log returns simplifies calculations and makes them statistically more robust, particularly for modeling and forecasting volatility. For example, if the price increases from $10 to $11 and then to $12, the simple return for each period is 10% and 9.09%, respectively. In contrast, the log return will be ln(11/10) + ln(12/11) which equals ln(12/10), simplifying calculations considerably. Learning how to calculate historical volatility effectively necessitates mastering this step.
The use of log returns in the calculation of historical volatility offers several advantages. First, log returns are approximately normally distributed, a crucial assumption for many statistical models used in finance. Second, log returns handle both large and small price changes in a consistent manner. Using the natural logarithm of the price ratio helps stabilize the variance, yielding more reliable volatility estimates. This is particularly critical when dealing with high-frequency data where small price fluctuations can significantly impact the simple return calculations. The formula for calculating log returns is straightforward, ensuring its easy implementation in various computational settings. This allows for efficient computation when working with large datasets and facilitates the application of statistical methods for advanced volatility analysis. Understanding this conversion is paramount to mastering how to calculate historical volatility accurately.
Consider a simplified example. Suppose the price of an asset is $100 on day 1 and $105 on day 2. The simple return is (105-100)/100 = 0.05 or 5%. The log return is ln(105/100) ≈ 0.0488 or approximately 4.88%. This seemingly minor difference becomes more pronounced over longer time periods and when dealing with larger price fluctuations. When you learn how to calculate historical volatility, the choice between simple and log returns significantly impacts accuracy, particularly in forecasting and risk management applications. Therefore, understanding the underlying properties and the correct application of log returns is critical for obtaining reliable volatility measures. The use of log returns, therefore, forms a crucial step in how to calculate historical volatility effectively and accurately.
How to Compute Historical Volatility Using Standard Deviation: A Step-by-Step Guide
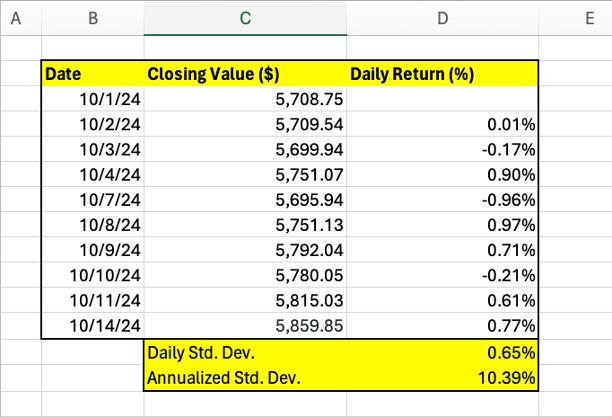
This section details how to calculate historical volatility using standard deviation. Understanding how to calculate historical volatility is crucial for assessing risk. The standard deviation measures the dispersion of a dataset around its mean. In the context of finance, this dataset comprises the log returns of an asset’s price. To calculate historical volatility, one first needs to determine the log returns. The formula for calculating the log return is: Log Return = ln(Pricet / Pricet-1), where Pricet is the current price and Pricet-1 is the previous period’s price. This method of calculating returns is preferred for its mathematical properties which make the data more suitable for statistical analysis. Learning how to calculate historical volatility accurately is a key skill for investors.
Once the log returns are calculated, the next step in how to calculate historical volatility involves computing the standard deviation. The formula for the standard deviation (σ) of a sample of log returns is: σ = √[ Σ(ri – μ)² / (n-1) ], where ri represents each individual log return, μ is the average of the log returns, and n is the number of observations. The (n-1) in the denominator indicates the use of the sample standard deviation, which is a more accurate estimate when dealing with a sample of data, rather than the entire population of data. This formula essentially quantifies the average distance of each log return from the mean. A higher standard deviation indicates greater volatility. This step in learning how to calculate historical volatility is critical for accurate risk assessment.
Let’s illustrate how to calculate historical volatility with an example. Suppose we have the following daily log returns for a stock: 0.01, 0.02, -0.01, 0.015, -0.005. First, calculate the average log return (μ): (0.01 + 0.02 – 0.01 + 0.015 – 0.005) / 5 = 0.006. Next, subtract the average from each log return, square the result, and sum the squares: [(0.01 – 0.006)² + (0.02 – 0.006)² + (-0.01 – 0.006)² + (0.015 – 0.006)² + (-0.005 – 0.006)²] = 0.000115. Finally, divide this sum by (n-1) = 4, take the square root, and multiply by 100% to express the result as a percentage: √(0.000115 / 4) * 100% ≈ 1.69%. This 1.69% represents the historical volatility of the stock over this period. Therefore, mastering how to calculate historical volatility allows for a quantified measure of price fluctuation. Remember to always use adjusted closing prices to account for corporate actions like stock splits or dividends when performing these calculations, improving the accuracy of how to calculate historical volatility.
Interpreting Your Results: What Does Volatility Actually Mean?
The calculated historical volatility represents the standard deviation of the log returns, expressed as a percentage. A higher percentage signifies greater price fluctuations and thus, higher risk. Conversely, a lower percentage indicates less price movement and lower risk. Understanding how to calculate historical volatility is crucial for interpreting these values accurately. For example, a historical volatility of 20% suggests that, on average, the asset’s price has fluctuated by approximately 20% annually. This information is invaluable for assessing risk tolerance and making informed investment decisions. Remember, a higher volatility doesn’t inherently mean an asset is bad; it simply means it’s riskier. High-volatility assets might offer higher potential returns, but they also carry a greater chance of significant losses. Investors with a higher risk tolerance might find such assets appealing, while more conservative investors would likely prefer lower-volatility options.
When using historical volatility in investment strategies, consider the time horizon. Volatility calculated from daily data will be higher than that calculated from monthly data, for the same asset. This is because daily price changes are inherently more volatile than monthly changes. The choice of data frequency depends on the investment strategy. Short-term traders might focus on daily volatility, while long-term investors might find monthly or even yearly data more relevant. Understanding how to calculate historical volatility for different time horizons allows for a nuanced risk assessment. Always consider context. A 20% volatility for a growth stock might be considered normal, while the same volatility for a blue-chip company could signal unusual market activity. The appropriate interpretation depends on the asset class and the prevailing market conditions. Accurate calculation and thoughtful interpretation are vital to harnessing the power of this key metric.
Furthermore, it is important to remember that historical volatility is just an estimate of future volatility. Past performance does not guarantee future results. While historical volatility provides valuable insights into an asset’s past price behavior, it doesn’t predict future price swings. Many factors can influence volatility, including economic conditions, market sentiment, and geopolitical events. Therefore, historical volatility should be considered alongside other factors when making investment decisions. Knowing how to calculate historical volatility is a crucial first step, but it’s only part of a larger process of thorough risk assessment. Investors should always diversify their portfolios to mitigate risks associated with high-volatility assets. They should also conduct thorough due diligence before investing in any asset, regardless of its volatility level.
Applying Your Knowledge: Real-World Examples of How to Calculate Historical Volatility
Understanding how to calculate historical volatility offers significant advantages in various financial applications. Portfolio managers utilize historical volatility to assess the risk associated with different asset classes. By calculating the historical volatility of individual stocks or bonds, a portfolio manager can build a diversified portfolio that aligns with the investor’s risk tolerance. Higher volatility stocks might contribute to higher potential returns but also increased risk, while lower volatility assets offer more stability. Knowing how to calculate historical volatility allows for a more nuanced understanding of these trade-offs.
Option pricing models heavily rely on historical volatility estimates. The Black-Scholes model, a cornerstone of options pricing, uses volatility as a key input. The higher the historical volatility of the underlying asset, the more expensive the options will generally be. This is because higher volatility implies a greater range of possible future prices, increasing the potential payoff for options buyers and the potential risk for options sellers. Therefore, understanding how to calculate historical volatility is essential for anyone involved in options trading or valuation.
Risk management professionals employ historical volatility in stress testing and scenario analysis. By calculating historical volatility over different time periods and under varying market conditions, risk managers can estimate potential losses under adverse scenarios. This aids in determining appropriate risk limits and developing effective hedging strategies. For instance, a bank might use historical volatility data to assess the risk associated with its loan portfolio and set aside adequate capital reserves. The ability to accurately calculate historical volatility is, therefore, crucial for prudent financial risk management. Knowing how to calculate historical volatility is a critical skill for anyone involved in managing financial risks effectively. Accurate calculations help inform investment decisions and risk mitigation strategies.
Advanced Techniques for Volatility Measurement
While the standard deviation method provides a foundational understanding of how to calculate historical volatility, more sophisticated techniques offer refined insights. Exponentially weighted moving averages (EWMA) represent a significant advancement. Unlike the standard deviation method which treats all past data points equally, EWMA assigns greater weight to more recent observations. This reflects the reality that recent price movements often hold more predictive power for future volatility than older data. The choice of weighting parameter determines the emphasis placed on recent data; a higher weight implies a greater sensitivity to recent price changes. Learning how to calculate historical volatility using EWMA requires understanding this weighting scheme and its impact on the resulting volatility estimate. The formula incorporates a decay factor that diminishes the influence of older data points. This approach is particularly useful in capturing shifts in market conditions more effectively than the standard deviation method.
Another powerful approach involves Generalized Autoregressive Conditional Heteroskedasticity (GARCH) models. GARCH models are particularly useful for predicting future volatility. These models account for both the persistence of volatility (volatility clustering) and the relationship between past volatility and current volatility. Unlike the standard deviation approach and EWMA, which are primarily descriptive, GARCH models are explicitly designed for forecasting. This is because they consider the conditional variance of asset returns. The conditional variance is the variance of returns given past information. Learning how to calculate historical volatility using GARCH models involves estimating the model parameters using statistical software. GARCH models offer a more nuanced understanding of volatility dynamics compared to the simpler methods described earlier.
Both EWMA and GARCH models offer advantages over the basic standard deviation method for how to calculate historical volatility. EWMA captures changing volatility more effectively. GARCH models provide forecasts and account for volatility clustering. However, these advanced techniques require specialized statistical software and a deeper understanding of statistical modeling. The choice of method depends on the specific application and the desired level of sophistication. For many applications, understanding the standard deviation approach provides a solid foundation before progressing to more complex methods. Mastering the basics of how to calculate historical volatility using standard deviation remains a critical first step.
Avoiding Common Pitfalls in Volatility Calculations
Accurately calculating historical volatility is crucial for informed investment decisions. However, several common mistakes can lead to inaccurate results and flawed interpretations. One frequent error involves using unreliable or inappropriate price data. Choosing a data source with known biases or using unadjusted closing prices can significantly skew the volatility calculation. Remember, how to calculate historical volatility accurately relies on using clean, adjusted closing prices from a reputable source. Data frequency also matters. Daily data provides a more granular view of price movements but introduces noise, potentially impacting the accuracy of how to calculate historical volatility. Conversely, using monthly data might smooth out short-term fluctuations, obscuring important aspects of volatility.
Another common pitfall stems from incorrectly applying the standard deviation formula or misinterpreting the results. Double-checking calculations is essential to avoid simple arithmetic errors. Understanding that historical volatility measures past price fluctuations, not future ones, is crucial. Many fall into the trap of extrapolating past volatility directly to future market behavior. This is unreliable. How to calculate historical volatility should be understood as a retrospective measure. The formula itself, while straightforward, requires precise input. Incorrectly calculating log returns, for instance, can propagate errors throughout the process. Using appropriate statistical software or tools helps mitigate this risk, as it automatically handles complex calculations and reduces the chance of human error. Therefore, understanding how to calculate historical volatility requires diligence and the right tools.
Finally, misinterpreting the calculated value is a prevalent mistake. The resulting percentage represents the historical standard deviation of log returns, providing a measure of past price variability. A high volatility value signifies greater price swings, indicating higher risk. A low value suggests less price variability and potentially lower risk. However, it’s vital to remember that historical volatility isn’t a perfect predictor of future volatility. Market conditions are dynamic, and unforeseen events can drastically impact price movements. Therefore, while understanding how to calculate historical volatility is essential, always consider its limitations and use it in conjunction with other analytical tools for a comprehensive risk assessment. Always strive for precision in how to calculate historical volatility to ensure your analysis is reliable and effective.