Understanding Average Investment Growth: A Practical Guide
Investment returns are a crucial measure of financial performance, reflecting the profit or loss generated by an investment over a specific period. Understanding how to accurately calculate average growth is paramount for investors seeking to evaluate past performance and project potential future returns. Averages provide a simplified view of complex data, enabling comparisons between different investments or across different timeframes. However, a simple arithmetic average, while easy to calculate, can often present a misleading picture of investment growth, particularly when returns fluctuate significantly from period to period. This is where understanding how to calculate geometric rate of return becomes essential.
The limitations of simple averages stem from their failure to account for the compounding effect of investment returns. For instance, an investment that increases by 50% in one year and decreases by 50% in the next will have an arithmetic average return of 0%. However, the investor has clearly lost money. This discrepancy highlights the need for a more sophisticated method that accurately reflects the actual compounded growth rate experienced by an investment. The geometric mean addresses this issue by considering the impact of compounding, providing a more realistic representation of long-term investment performance. Therefore, knowing how to calculate geometric rate of return is a necessary skill.
This guide will delve into the concept of the geometric mean, explaining its significance in investment analysis and providing a step-by-step approach on how to calculate geometric rate of return. By understanding the nuances of this calculation, investors can gain a more accurate perspective on their investment performance, enabling them to make more informed decisions. We will explore the formula, illustrate its application with examples, and demonstrate how to easily calculate it using spreadsheet software. Understanding how to calculate geometric rate of return empowers investors to assess performance more effectively.
What is Geometric Average Return and Why Does It Matter?
The geometric average return is a method used to determine the average rate of return of an investment over a specified period. It offers a more accurate picture of investment performance than a simple arithmetic average, especially when returns fluctuate significantly. The key purpose of the geometric average return is to represent the actual compounded growth rate experienced by an investment. This is crucial for understanding the real performance of an investment over time. Knowing how to calculate geometric rate of return is essential for investors.
To understand the importance, it’s useful to distinguish between the arithmetic and geometric means. The arithmetic mean is calculated by summing the returns and dividing by the number of periods. While easy to calculate, it can be misleading when dealing with investment returns. For instance, an investment that increases by 100% in one year and decreases by 50% the next would have an arithmetic mean of 25%. However, the actual compounded return is 0%, as the investor ends up with the same initial investment. The geometric mean accurately reflects this reality.
When should each be used? The arithmetic mean is appropriate for forecasting returns in a single period, as it represents the expected value. However, the geometric mean is better suited for evaluating past performance, especially over multiple periods, as it reflects the actual compounded growth. Understanding how to calculate geometric rate of return provides investors with a valuable tool for assessing the true performance of their investments and making informed decisions. This is especially useful when comparing investment options with varying return patterns. By focusing on the compounded growth rate, investors can gain a clearer understanding of the long-term potential of their investments. For evaluating true investment return, knowing how to calculate geometric rate of return is imperative.
How to Determine Geometric Mean of Returns: A Step-by-Step Approach
To understand how to calculate geometric rate of return, it’s essential to break down the process into manageable steps. The geometric mean provides a more accurate measure of investment performance than a simple arithmetic average, especially when dealing with fluctuating returns over multiple periods. This section offers a clear, step-by-step guide to calculating the geometric mean of returns.
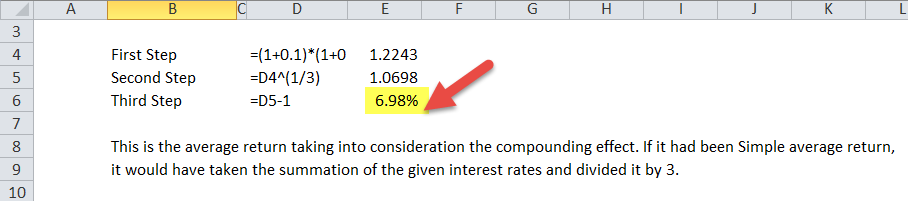
The formula for the geometric mean return is as follows: Geometric Mean = [(1 + Return₁) * (1 + Return₂) * … * (1 + Returnₙ)]^(1/n) – 1, where Return₁, Return₂, …, Returnₙ are the returns for each period, and n is the number of periods. To begin, add 1 to each return percentage. This converts each return into a growth factor. For example, a 10% return becomes 1.10, and a -5% return becomes 0.95. Next, multiply all the growth factors together. After multiplying the growth factors, raise the result to the power of 1/n, where n is the number of periods. This is equivalent to taking the nth root of the product. Finally, subtract 1 from the result to obtain the geometric mean return. This gives you the average compounded return over the period. Understanding how to calculate geometric rate of return using this formula is fundamental for investment analysis.
Let’s illustrate how to calculate geometric rate of return with an example. Suppose an investment has the following annual returns over three years: 15%, -10%, and 8%. First, convert these returns into growth factors: 1.15, 0.90, and 1.08. Multiply these growth factors together: 1.15 * 0.90 * 1.08 = 1.1124. Next, raise this product to the power of 1/3 (or take the cube root): 1.1124^(1/3) ≈ 1.036. Finally, subtract 1: 1.036 – 1 = 0.036, or 3.6%. Therefore, the geometric mean return for this investment over the three years is approximately 3.6%. This example showcases how to calculate geometric rate of return in a practical scenario, highlighting its utility in evaluating investment performance across different periods. Remember that accurately knowing how to calculate geometric rate of return is essential for comparing investment options and assessing true growth.
Illustrative Examples of Geometric Return Calculation
To further clarify how to calculate geometric rate of return, let’s examine a few practical scenarios. These examples will demonstrate the calculation of the geometric mean under varying conditions, including both positive and negative returns. Understanding these examples is crucial for investors seeking to accurately assess their investment performance. Keep in mind that the geometric mean provides a more accurate picture of compounded growth than a simple arithmetic average. This is particularly important when returns fluctuate significantly over time. Let’s explore the following scenarios to understand how to calculate geometric rate of return.
Example 1: Consistent Positive Returns: Consider an investment that yields the following annual returns over three years: 10%, 15%, and 20%. To calculate the geometric rate of return, we first add 1 to each return (1.10, 1.15, 1.20). Next, we multiply these values together (1.10 * 1.15 * 1.20 = 1.518). Then, we take the cube root of the result (since there are three periods), which is approximately 1.148. Finally, we subtract 1 to express the result as a percentage (1.148 – 1 = 0.148, or 14.8%). Therefore, the geometric average return for this investment is 14.8%. This represents the true compounded annual growth rate. This shows how to calculate geometric rate of return.
Example 2: Positive and Negative Returns: Imagine an investment with the following annual returns over four years: 25%, -10%, 15%, and -5%. The steps to calculate geometric rate of return are as follows: Add 1 to each return (1.25, 0.90, 1.15, 0.95). Multiply these values together (1.25 * 0.90 * 1.15 * 0.95 = 1.233). Take the fourth root of the result (since there are four periods), which is approximately 1.053. Subtract 1 to express the result as a percentage (1.053 – 1 = 0.053, or 5.3%). In this case, the geometric average return is 5.3%. Note how the negative returns significantly impact the overall compounded growth rate. This example highlights the importance of the geometric mean when dealing with fluctuating returns. Comparing this to the arithmetic mean would reveal a higher, and potentially misleading, average return. This comparison stresses how to calculate geometric rate of return.
Calculating Geometric Mean with Excel and Google Sheets
Spreadsheet software like Excel and Google Sheets simplifies how to calculate geometric rate of return. These tools offer built-in functions that automate the calculation, saving time and reducing the risk of manual errors. To determine the geometric mean in Excel or Google Sheets, the `GEOMEAN` function is used.
The syntax for the `GEOMEAN` function is straightforward: `=GEOMEAN(number1, number2, …).` However, it’s crucial to input the returns in the correct format. The formula requires the returns to be expressed as (1 + return), where “return” is the percentage return for each period expressed as a decimal. For instance, a 10% return should be entered as 1.10. So, if you have returns of 10%, -5%, and 15%, the formula would look like this: `=GEOMEAN(1.10, 0.95, 1.15)`. This calculates the geometric mean of the total return. To get the geometric rate of return, you must subtract 1 from the result. Therefore, the complete formula is: `=GEOMEAN(1.10, 0.95, 1.15)-1`. After entering the formula, format the cell as a percentage to display the result as a percentage return.
For those seeking how to calculate geometric rate of return efficiently, spreadsheets are invaluable. Imagine annual returns of 8%, 12%, -3%, and 5%. In an Excel or Google Sheets cell, you would type `=GEOMEAN(1.08,1.12,0.97,1.05)-1`. The result would be approximately 0.053 or 5.3%, representing the geometric mean return. This demonstrates how easily one can calculate geometric rate of return using these tools. Remember that past performance doesn’t guarantee future returns. Always review your data for accuracy before performing the calculation.
The Significance of Geometric Return in Investment Analysis
The geometric mean plays a vital role in investment analysis, offering a more realistic perspective on investment performance than simple averages. Understanding how to calculate geometric rate of return is crucial for making informed financial decisions. It directly addresses the impact of compounding, accurately reflecting the actual growth experienced by an investment over time, especially when returns fluctuate. By calculating the geometric rate of return, investors gain a clearer understanding of their investment’s true performance.
One of the most important practical implications of using the geometric mean lies in its ability to provide a more accurate representation of past performance, which can then be used to estimate potential future growth. While past performance is never a guarantee, the geometric mean offers a less distorted view compared to the arithmetic mean, which can be easily skewed by unusually high returns in certain periods. Learning how to calculate geometric rate of return empowers investors to see beyond superficial numbers and assess the true compounded growth.
Furthermore, the geometric mean is invaluable when comparing different investment options. Consider two investments with similar arithmetic means. One might exhibit consistent, moderate returns, while the other experiences high volatility with significant gains and losses. The investment with consistent returns will invariably have a higher geometric mean, signaling its superior long-term performance and lower risk profile. Therefore, knowing how to calculate geometric rate of return enables investors to differentiate between seemingly similar investments and select those that offer a more stable and sustainable growth trajectory. This enhanced understanding helps investors make better choices aligned with their risk tolerance and financial goals, contributing to more successful investment outcomes. The geometric mean offers a more nuanced and informative comparison, helping investors understand how to calculate geometric rate of return for better decision-making.
Limitations of Relying Solely on Geometric Average
While the geometric mean provides a valuable perspective on investment performance, it’s crucial to acknowledge its limitations. Relying solely on this metric can paint an incomplete picture and potentially lead to flawed investment decisions. The geometric mean, in essence, presents a historical average and does not guarantee future returns. Market conditions are dynamic, and past performance is not necessarily indicative of future results.
One significant limitation is that the geometric mean doesn’t account for risk or volatility. Two investments might have the same geometric mean return over a period, but one could have experienced significantly larger swings in value than the other. An investor primarily focused on stability might prefer the investment with lower volatility, even if its geometric mean is slightly lower. Furthermore, the geometric mean doesn’t consider the timing of cash flows, such as deposits or withdrawals, which can significantly impact an investment’s overall return. It’s important to understand how to calculate geometric rate of return, but it’s equally important to understand its limitations.
Therefore, the geometric mean should be used in conjunction with other performance metrics and a thorough understanding of the investment’s characteristics. Factors like standard deviation (a measure of volatility), Sharpe ratio (a risk-adjusted return measure), and consideration of investment goals and risk tolerance are all essential components of a comprehensive investment analysis. While understanding how to calculate geometric rate of return is a useful skill, remember that it’s just one piece of the puzzle. A balanced perspective is paramount for making informed investment choices. Ignoring the limitations of the geometric mean and not considering other relevant factors could lead to an inaccurate assessment of an investment’s true potential and associated risks. Investors should always remember that knowing how to calculate geometric rate of return is not enough to guarantee investment success.
Geometric Return vs. Other Performance Metrics
Understanding how to calculate geometric rate of return is crucial, but it’s equally important to differentiate it from other investment performance metrics. The arithmetic mean, a simple average, is often used but can be misleading when dealing with investment returns over time. It doesn’t accurately reflect the compounded growth rate because it doesn’t account for the effects of volatility. For instance, a 20% gain followed by a 20% loss doesn’t result in a net 0% change in investment value. The geometric mean provides a more accurate picture in such scenarios.
Another important metric is the Compound Annual Growth Rate (CAGR). CAGR is essentially a specific application of the geometric mean, calculating the average annual growth rate of an investment over a specified period, assuming profits are reinvested during the term of the investment. While CAGR provides a smoothed average annual return, it doesn’t reflect the actual year-to-year volatility. Both geometric mean and CAGR are useful for evaluating past performance and projecting potential future growth, but they shouldn’t be the sole determinants of investment decisions. Knowing how to calculate geometric rate of return and CAGR offers a more complete understanding.
Time-weighted return is yet another performance metric. It measures the performance of an investment portfolio, removing the impact of cash flows (deposits and withdrawals) made by the investor. This is particularly useful for evaluating the investment manager’s skill, as it isolates their performance from the timing of investor contributions. Unlike the geometric mean, which focuses on the overall compounded growth, the time-weighted return assesses the portfolio’s returns at different points in time, weighting them equally regardless of the amount of money invested at each point. Choosing the right metric depends on the specific question being asked. To effectively analyze investment performance, investors should understand how to calculate geometric rate of return, along with the strengths and weaknesses of arithmetic mean, CAGR, and time-weighted return.