What is Delta and Why is it Important?
In various fields, including finance, science, and engineering, the concept of delta plays a crucial role in understanding and analyzing complex systems. At its core, delta represents a change or difference in a particular quantity or value. In essence, it measures the extent of a variation, which can have significant implications in real-world scenarios. For instance, in finance, delta is used to calculate the rate of change of an option’s price with respect to the underlying asset’s price. This metric is vital in options trading, risk management, and portfolio optimization. In science and engineering, delta is employed to quantify changes in physical quantities, such as temperature, pressure, or velocity, which is essential in research and development. Understanding delta is vital in making informed decisions, as it provides valuable insights into the behavior of complex systems. By grasping the concept of delta, individuals can better navigate uncertainty and make data-driven decisions. In this article, we will delve into the world of delta calculation, exploring its significance, applications, and importance in various fields, including learning how to calculate a delta in different contexts.
Understanding the Formula: A Step-by-Step Guide
The delta calculation formula is a fundamental concept in understanding how to calculate a delta. The formula is typically represented as Δ = (V2 – V1) / (X2 – X1), where Δ represents the delta, V1 and V2 are the initial and final values, and X1 and X2 are the initial and final points of reference. To break it down further, the numerator (V2 – V1) calculates the change in value, while the denominator (X2 – X1) represents the change in the point of reference. By dividing the change in value by the change in the point of reference, the delta calculation formula provides a precise measure of the rate of change. In practical applications, understanding each component of the formula is crucial in accurately calculating delta. For instance, in finance, the formula is used to calculate the rate of change of an option’s price with respect to the underlying asset’s price. In science and engineering, the formula is employed to quantify changes in physical quantities, such as temperature, pressure, or velocity. By mastering the delta calculation formula, individuals can unlock the secrets of complex systems and make informed decisions.
How to Calculate Delta in Finance: A Practical Approach
In finance, delta calculation plays a vital role in understanding the behavior of options and derivatives. To calculate delta in finance, one must first understand the concept of options and their underlying assets. An option’s delta represents the rate of change of its price with respect to the underlying asset’s price. This metric is crucial in options trading, risk management, and portfolio optimization. For instance, a call option with a delta of 0.5 indicates that for every $1 increase in the underlying asset’s price, the option’s price will increase by $0.50. To calculate delta in finance, traders and investors can use the Black-Scholes model, which provides a mathematical framework for estimating the delta of an option. The formula for calculating delta using the Black-Scholes model is Δ = N(d1), where N(d1) is the cumulative distribution function of the standard normal distribution. By mastering how to calculate a delta in finance, individuals can make informed investment decisions, manage risk more effectively, and optimize their portfolios for maximum returns.
In practice, delta calculation is used in various financial applications, such as hedging, arbitrage, and speculation. For example, a hedge fund manager may use delta calculation to determine the optimal hedge ratio for a portfolio of options. Similarly, a trader may use delta calculation to identify arbitrage opportunities in the market. By understanding how to calculate a delta in finance, individuals can gain a competitive edge in the markets and make more informed investment decisions.
Delta Calculation in Science and Engineering: Real-World Applications
In the realm of science and engineering, delta calculation plays a vital role in understanding and quantifying changes in physical quantities. In physics, delta calculation is used to measure the change in velocity, acceleration, and energy of an object. For instance, in a projectile motion problem, delta calculation can be used to determine the change in velocity of an object under the influence of gravity. In chemistry, delta calculation is employed to quantify the change in concentration of reactants and products in a chemical reaction. In materials science, delta calculation is used to study the change in properties of materials under different conditions, such as temperature and pressure.
In engineering, delta calculation is used to design and optimize systems, such as mechanical, electrical, and civil engineering systems. For example, in mechanical engineering, delta calculation can be used to determine the change in stress and strain of a material under different loads. In electrical engineering, delta calculation can be used to analyze the change in voltage and current in a circuit. By understanding how to calculate a delta in science and engineering, researchers and engineers can make more accurate predictions, optimize system performance, and improve overall efficiency.
In addition, delta calculation is used in various scientific and engineering applications, such as signal processing, image processing, and data analysis. In signal processing, delta calculation is used to analyze the change in signal amplitude and frequency. In image processing, delta calculation is used to quantify the change in image intensity and contrast. In data analysis, delta calculation is used to identify trends and patterns in data. By mastering how to calculate a delta in science and engineering, individuals can gain a deeper understanding of complex systems and make more informed decisions.
Common Mistakes to Avoid When Calculating Delta
When calculating delta, it’s essential to avoid common mistakes that can lead to inaccurate results and misinformed decisions. One of the most critical errors is incorrect formula application. This can occur when the wrong formula is used or when the formula is applied incorrectly. For instance, in finance, using the wrong delta calculation formula can result in incorrect risk assessments and portfolio optimizations. To avoid this mistake, it’s crucial to understand the underlying assumptions and limitations of the formula and to apply it correctly.
Another common mistake is data errors. Inaccurate or incomplete data can lead to incorrect delta calculations, which can have significant consequences in fields such as finance and engineering. To avoid data errors, it’s essential to ensure that the data is accurate, complete, and relevant to the calculation. Additionally, data should be regularly updated and validated to ensure that the delta calculation is based on the most recent and accurate information.
Misinterpretation of results is another common mistake to avoid when calculating delta. This can occur when the results are not properly understood or when they are misapplied. For example, in science and engineering, misinterpreting the results of a delta calculation can lead to incorrect conclusions and decisions. To avoid misinterpretation, it’s essential to understand the context and limitations of the calculation and to interpret the results correctly.
Other common mistakes to avoid when calculating delta include ignoring underlying assumptions, failing to consider external factors, and neglecting to validate results. By understanding how to calculate a delta accurately and avoiding these common mistakes, individuals can ensure that their calculations are reliable and informative, leading to better decision-making and risk management.
Delta Calculation Tools and Resources: A Comprehensive Review
When it comes to calculating delta, having the right tools and resources can make all the difference. With the abundance of options available, it’s essential to understand the features, advantages, and limitations of each tool to make an informed decision. In this section, we’ll review and compare popular tools, software, and online resources for delta calculation, highlighting their strengths and weaknesses.
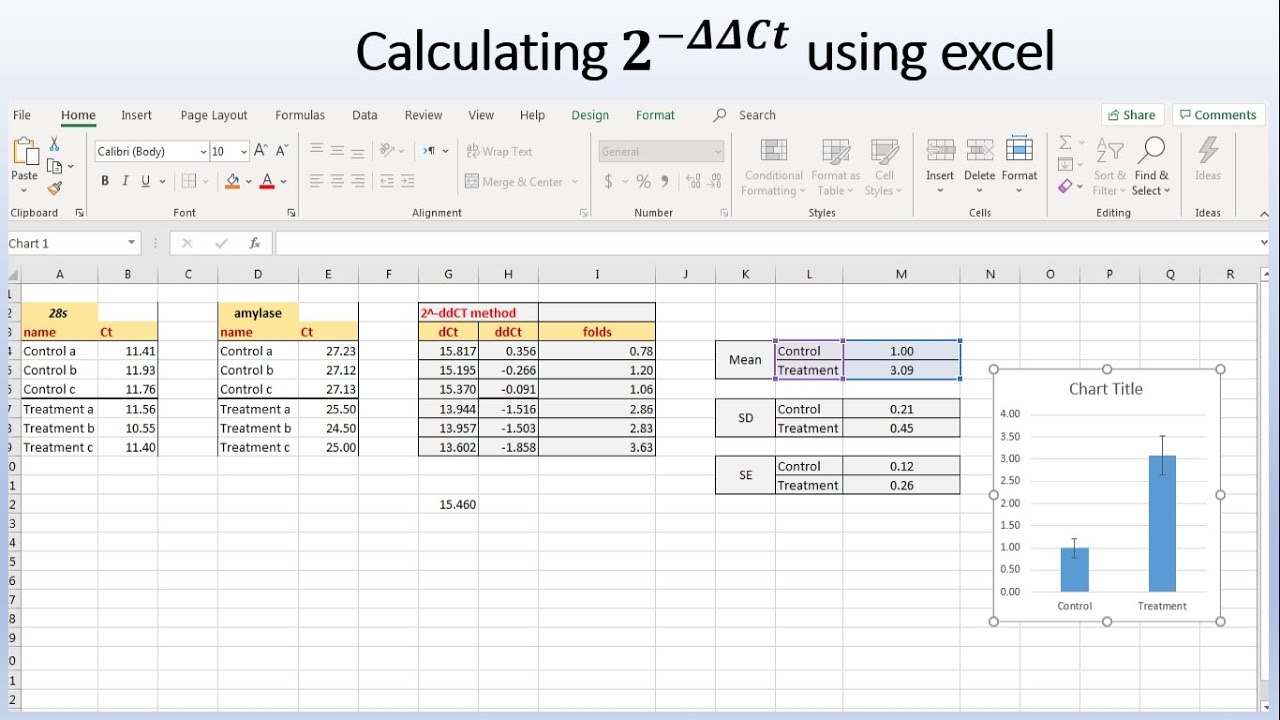
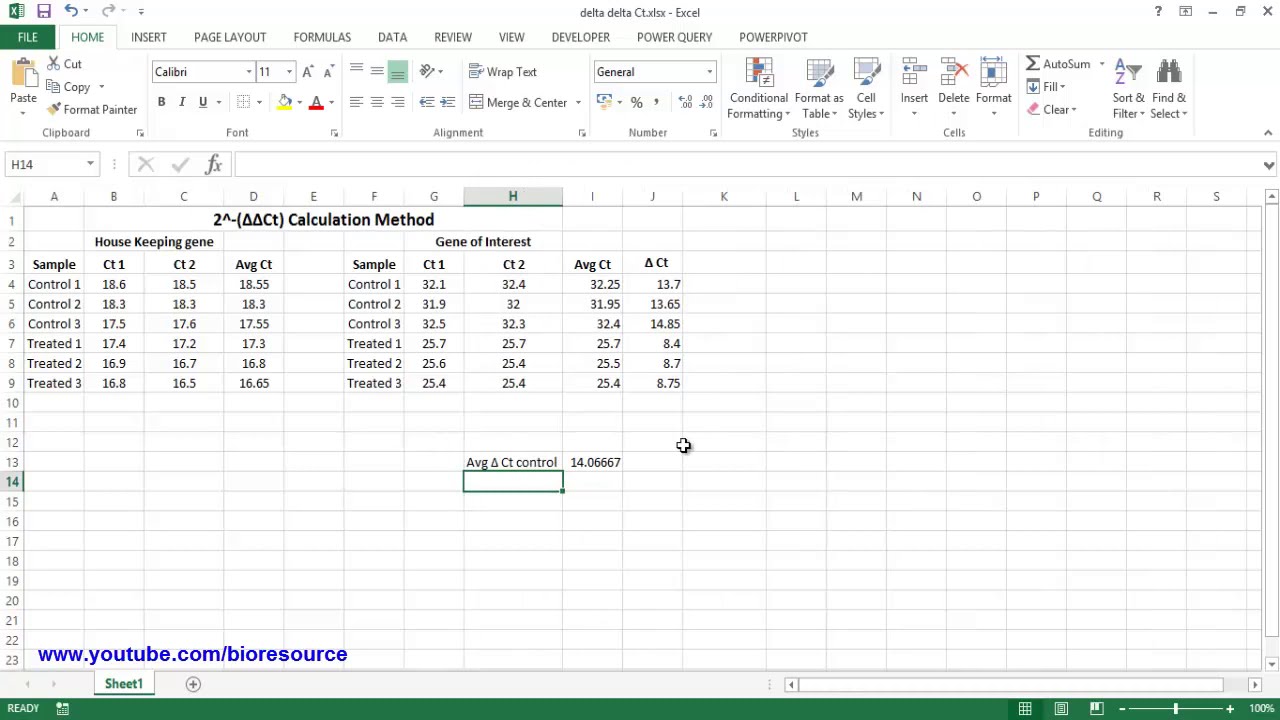
One of the most popular tools for delta calculation is Microsoft Excel. Excel offers a range of built-in functions and formulas that can be used to calculate delta, including the delta function, which can be used to calculate the change in a value over time. Additionally, Excel’s data analysis tools and add-ins, such as Solver and Analysis ToolPak, can be used to perform more complex delta calculations.
Another popular tool for delta calculation is Python, a programming language that offers a range of libraries and modules, including NumPy and SciPy, that can be used to perform delta calculations. Python’s flexibility and customization options make it an ideal choice for complex and nuanced delta calculations.
Online resources, such as Wolfram Alpha and Symbolab, also offer delta calculation tools and resources. These resources provide step-by-step guides and examples, making it easy to learn how to calculate a delta and apply it in different contexts. Additionally, online forums and communities, such as Reddit’s r/math and r/finance, offer a wealth of knowledge and expertise, providing users with a platform to ask questions and share knowledge.
Specialized software, such as Matlab and Mathematica, also offer delta calculation tools and resources. These software packages provide advanced features and functionality, making them ideal for complex and high-level delta calculations.
In conclusion, when it comes to calculating delta, having the right tools and resources is essential. By understanding the features, advantages, and limitations of each tool, individuals can make an informed decision and choose the tool that best suits their needs. Whether it’s Microsoft Excel, Python, online resources, or specialized software, mastering how to calculate a delta has never been easier.
Advanced Delta Calculation Techniques: Taking it to the Next Level
While understanding the basics of delta calculation is essential, mastering advanced techniques can take your skills to the next level. In this section, we’ll explore advanced delta calculation techniques, including Monte Carlo simulations, sensitivity analysis, and scenario planning, and how they can be applied in complex and nuanced applications.
Monte Carlo simulations are a powerful tool for advanced delta calculation. By running multiple simulations, users can estimate the probability of different outcomes and calculate the delta accordingly. This technique is particularly useful in finance, where it can be used to estimate the risk of investment portfolios and calculate the delta of options and derivatives.
Sensitivity analysis is another advanced technique for delta calculation. This involves analyzing how changes in one variable affect the delta of another variable. By understanding the sensitivity of different variables, users can identify the most critical factors affecting the delta and make informed decisions accordingly.
Scenario planning is a technique that involves creating hypothetical scenarios to estimate the delta of different outcomes. This technique is particularly useful in science and engineering, where it can be used to estimate the delta of different variables under different scenarios. By understanding the delta of different scenarios, users can identify the most critical factors affecting the outcome and make informed decisions accordingly.
Other advanced delta calculation techniques include bootstrapping, which involves resampling data to estimate the delta, and machine learning algorithms, which can be used to estimate the delta of complex systems. By mastering these advanced techniques, users can take their delta calculation skills to the next level and make more informed decisions in a variety of fields.
When it comes to how to calculate a delta, understanding advanced techniques can provide a competitive edge. By applying these techniques in real-world scenarios, users can gain a deeper understanding of complex systems and make more informed decisions. Whether it’s in finance, science, or engineering, mastering advanced delta calculation techniques can take your skills to the next level.
Conclusion: Mastering Delta Calculation for Informed Decision-Making
In conclusion, mastering the art of delta calculation is crucial for making informed decisions in various fields, including finance, science, and engineering. By understanding how to calculate a delta, individuals can gain a deeper insight into complex systems and make more accurate predictions. Whether it’s in options trading, risk management, or portfolio optimization, delta calculation plays a vital role in minimizing risk and maximizing returns.
Throughout this article, we’ve explored the concept of delta, its significance, and its applications in real-world scenarios. We’ve also delved into advanced delta calculation techniques, including Monte Carlo simulations, sensitivity analysis, and scenario planning. By mastering these techniques, individuals can take their delta calculation skills to the next level and make more informed decisions.
The importance of accurate delta calculation cannot be overstated. Inaccurate delta calculations can lead to poor decision-making, significant financial losses, and even catastrophic consequences in scientific and engineering applications. Therefore, it’s essential to understand how to calculate a delta accurately and apply it in different contexts.
By mastering delta calculation, individuals can gain a competitive edge in their respective fields. They can make more informed decisions, minimize risk, and maximize returns. Whether it’s in finance, science, or engineering, delta calculation is an essential skill that can make all the difference.
In conclusion, mastering the art of delta calculation is a valuable skill that can have a significant impact on decision-making and risk management. By understanding how to calculate a delta and applying it in different contexts, individuals can make more informed decisions and achieve their goals.