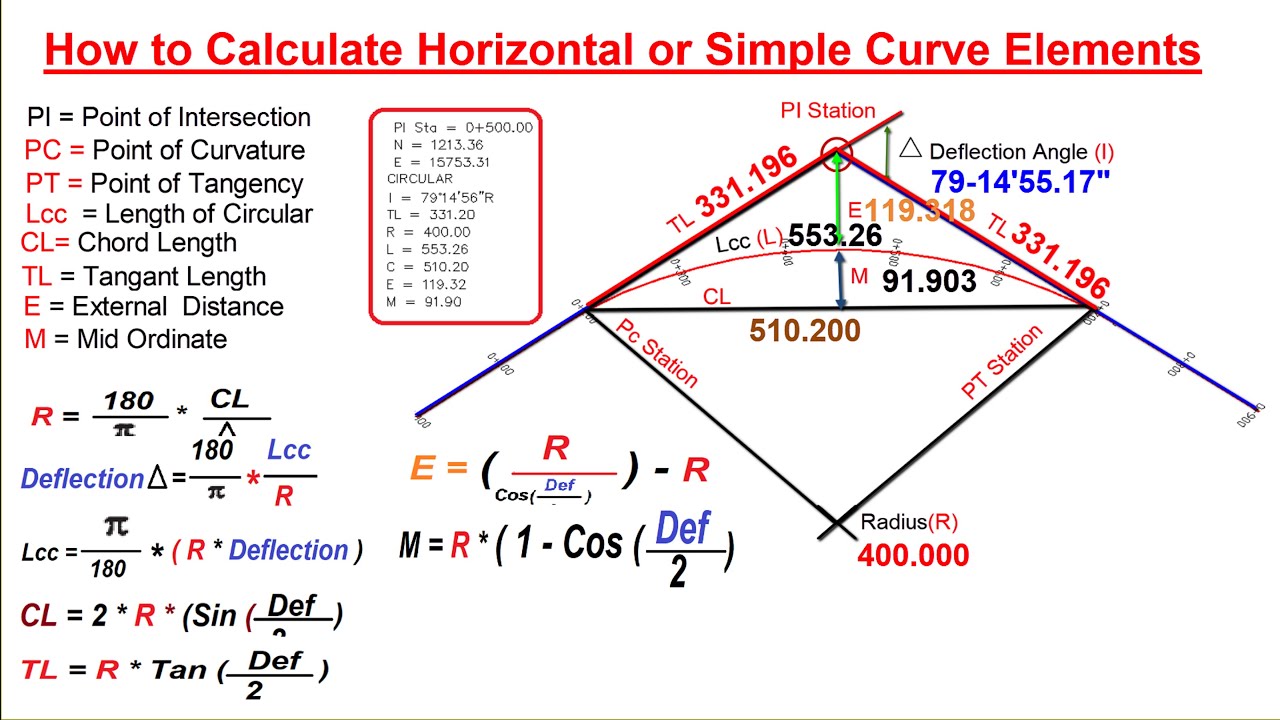
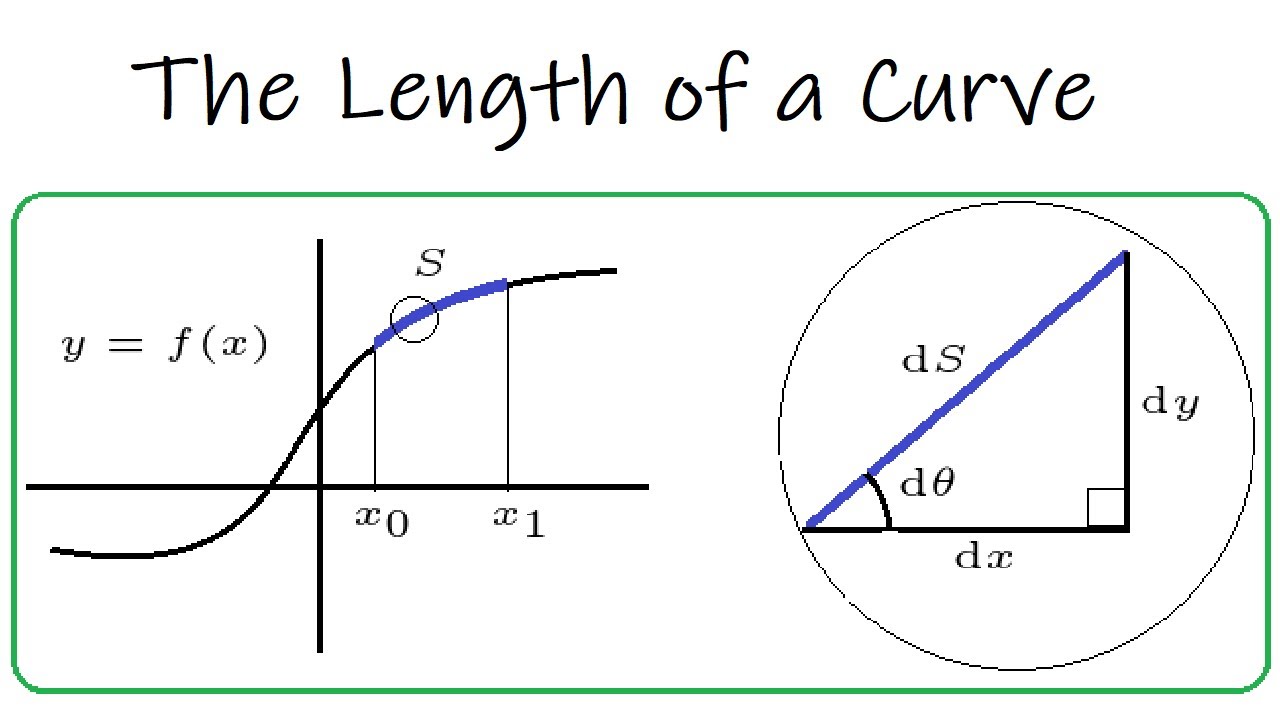
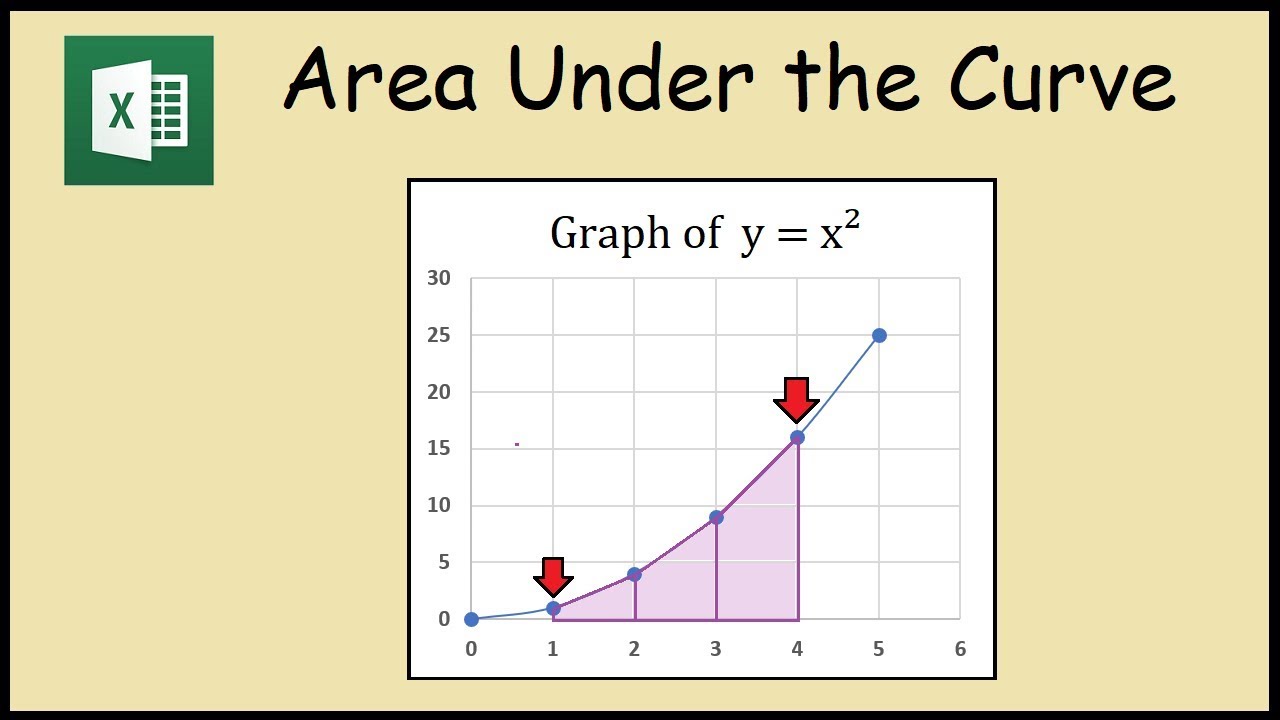
What is a Curve and Why is it Important?
In the realm of mathematics, physics, and engineering, curves play a vital role in understanding and analyzing complex phenomena. A curve, in essence, is a set of points that can be defined by a mathematical equation or function. It can be a straight line, a parabola, a circle, or any other shape that can be described using mathematical concepts. The importance of curves lies in their ability to model real-world phenomena, such as the trajectory of a projectile, the shape of a bridge, or the growth pattern of a population. Accurate calculation of curves is vital in these fields, as it enables professionals to make informed decisions, predict outcomes, and optimize systems. Understanding how to calculate a curve is crucial in unlocking the secrets of these phenomena, and this guide will provide a comprehensive overview of the process.
Understanding the Different Types of Curves
Curves come in various shapes and forms, each with its unique characteristics and applications. In this section, we will delve into the different types of curves, including linear, quadratic, and polynomial curves. Understanding these types is crucial in determining how to calculate a curve accurately. Linear curves, for instance, are straight lines that can be defined by a single slope and y-intercept. They are commonly used in physics to model the motion of objects. Quadratic curves, on the other hand, are parabolas that can be defined by a quadratic equation. They are often used in engineering to design bridges and other structures. Polynomial curves, which include cubic, quartic, and higher-degree curves, are used in computer graphics and data analysis to model complex phenomena. By recognizing the type of curve, professionals can choose the appropriate method for calculating it, ensuring accurate results and informed decision-making.
How to Calculate a Curve: The Basics
Calculating a curve involves a series of steps that help professionals understand and analyze complex phenomena. To master the art of curve calculation, it is essential to follow a structured approach. The first step in how to calculate a curve is to identify the type of curve, which can be linear, quadratic, polynomial, or other types. Once the type of curve is determined, the next step is to determine the equation of the curve, which can be done using various methods such as the point-slope form, slope-intercept form, or standard form. After determining the equation, the curve can be plotted on a graph, allowing professionals to visualize and analyze the data. By following these basic steps, professionals can accurately calculate curves and make informed decisions in their respective fields. In the following sections, we will delve deeper into each of these steps, providing a comprehensive guide on how to calculate a curve.
Determining the Equation of a Curve
Determining the equation of a curve is a crucial step in how to calculate a curve. There are several methods to determine the equation of a curve, each with its own strengths and weaknesses. The point-slope form, for instance, is useful when the slope and a point on the curve are known. This form is expressed as y – y1 = m(x – x1), where m is the slope and (x1, y1) is a point on the curve. The slope-intercept form, on the other hand, is useful when the slope and y-intercept are known. This form is expressed as y = mx + b, where m is the slope and b is the y-intercept. The standard form, also known as the general form, is expressed as Ax + By + C = 0, where A, B, and C are constants. By understanding these different forms and when to apply them, professionals can accurately determine the equation of a curve and proceed with plotting and analyzing the data. In the next section, we will provide guidance on how to plot a curve accurately, including tips on choosing the right scale and identifying key features.
Plotting a Curve: Tips and Tricks
Once the equation of a curve is determined, the next step in how to calculate a curve is to plot it accurately. Plotting a curve involves more than just putting points on a graph; it requires a deep understanding of the curve’s behavior and key features. To plot a curve effectively, it is essential to choose the right scale, label axes correctly, and identify key features such as maxima and minima. A well-plotted curve can reveal valuable insights into the underlying data, allowing professionals to make informed decisions. For instance, in data analysis, a curve can help identify trends and patterns, while in engineering, it can help design more efficient systems. By following best practices for plotting a curve, professionals can ensure that their calculations are accurate and reliable. In the next section, we will explore the various real-world applications of curve calculation, highlighting its significance in fields such as architecture, engineering, and data analysis.
Real-World Applications of Curve Calculation
Curve calculation has numerous real-world applications across various fields, including architecture, engineering, and data analysis. In architecture, curve calculation is used to design visually appealing and structurally sound buildings, bridges, and other infrastructure. For instance, architects use curves to create sweeping arches, domes, and other complex shapes that are both aesthetically pleasing and functional. In engineering, curve calculation is used to optimize system performance, such as in the design of roller coasters, where curves are used to create a smooth and thrilling ride. In data analysis, curve calculation is used to model complex phenomena, such as population growth, financial markets, and weather patterns. By understanding how to calculate a curve, professionals in these fields can make informed decisions, improve designs, and drive innovation. In the next section, we will discuss common mistakes to avoid when calculating a curve, highlighting the importance of accuracy and attention to detail.
Common Mistakes to Avoid When Calculating a Curve
When learning how to calculate a curve, it is essential to be aware of common mistakes that can occur, leading to inaccurate results. One common error is incorrect equation formation, which can result from misunderstanding the type of curve or incorrectly applying the equation formula. Another mistake is inaccurate plotting, which can occur when the scale is not chosen correctly or the axes are not labeled properly. Additionally, failing to identify key features such as maxima and minima can lead to a lack of understanding of the curve’s behavior. To avoid these mistakes, it is crucial to carefully follow the steps involved in calculating a curve, including identifying the type of curve, determining the equation, and plotting the curve accurately. By being mindful of these common mistakes, professionals can ensure that their calculations are accurate and reliable, leading to better decision-making and more effective problem-solving. In the next section, we will explore advanced curve calculation techniques, including numerical methods and computer-aided design, and provide examples of their applications.
Advanced Curve Calculation Techniques
Once the basics of how to calculate a curve are mastered, it’s time to explore more advanced techniques that can help professionals take their curve calculation skills to the next level. One such technique is numerical methods, which involve using numerical algorithms to approximate the curve. This method is particularly useful when dealing with complex curves that cannot be easily expressed in analytical form. Another advanced technique is computer-aided design (CAD), which uses software to create and manipulate curves in a digital environment. CAD is widely used in fields such as architecture, engineering, and product design, where precise curve calculation is critical. Additionally, advanced curve calculation techniques can be used in data analysis to model complex phenomena, such as population growth or financial markets. By learning these advanced techniques, professionals can expand their toolkit and tackle more complex curve calculation challenges. With a solid understanding of how to calculate a curve and the ability to apply advanced techniques, professionals can unlock new possibilities in their field and drive innovation.