Understanding Random Walks and Stock Price Fluctuations
The simplest model for stock price movements is a random walk. This assumes price changes are independent and identically distributed, meaning each price change is completely random and unrelated to previous changes. However, this model has significant limitations. A simple random walk, for example, allows for negative stock prices, which is unrealistic. Real-world stock prices tend to exhibit a persistent upward trend over the long term, a characteristic not captured by a simple random walk. Moreover, the volatility of stock prices—the magnitude of their fluctuations—often changes over time. Therefore, a more sophisticated model is needed to accurately capture the dynamics of geometric brownian motion stock price movements. Geometric Brownian Motion (GBM) offers a more realistic and widely used alternative. The geometric brownian motion stock price model addresses these shortcomings by incorporating both a trend and volatility. This improved model better reflects the behavior of actual stock prices, making it a valuable tool for financial modeling and prediction.
Unlike a simple arithmetic random walk, where price changes are added directly to the previous price, GBM models price changes as proportional to the current price. This multiplicative nature prevents stock prices from becoming negative. This crucial difference reflects the reality of financial markets; a 10% increase from $100 is $10, while a 10% increase from $1 is only $0.10. The proportional change accounts for the compounding effect seen in investment returns, a feature missing in simpler models. This fundamental characteristic of GBM makes it particularly suitable for modeling asset prices, where the percentage change is often more meaningful than the absolute change. To successfully implement GBM in financial analysis, a deep understanding of its underlying mathematical framework is essential.
The geometric brownian motion stock price model’s superiority over simpler models lies in its ability to capture both the upward trend (drift) and the random fluctuations (volatility) observed in real-world stock prices. This makes it a powerful tool for various applications, including option pricing, portfolio management, and risk assessment. By incorporating these key features, GBM provides a significantly more accurate and robust representation of asset price behavior than simple random walk models. This improved accuracy enhances the reliability of financial models that utilize it and leads to more informed decision-making in the world of finance.
Introducing Geometric Brownian Motion: The Mathematical Foundation
Geometric Brownian Motion (GBM) provides a powerful mathematical model for simulating the stochastic behavior of stock prices. It elegantly captures the random fluctuations inherent in financial markets. The model’s foundation lies in a stochastic differential equation (SDE) that describes how the stock price changes over an infinitesimally small time interval. This equation is expressed as dS = μSdt + σSdz, where S represents the stock price, μ denotes the drift (average rate of return), σ signifies the volatility (measure of price fluctuation), dt represents a small time increment, and dz represents an increment of a Wiener process (a mathematical representation of random noise). Understanding this equation is key to grasping the dynamics of geometric brownian motion stock price movements.
The Wiener process, also known as Brownian motion, introduces the randomness into the model. It’s a continuous-time stochastic process with independent and normally distributed increments. The drift parameter, μ, determines the average trend of the stock price. A positive drift indicates an upward trend, while a negative drift indicates a downward trend. Volatility, σ, quantifies the magnitude of random fluctuations around the average trend. Higher volatility implies greater price uncertainty. The interplay between drift and volatility dictates the overall path of the geometric brownian motion stock price. The multiplication of S by both μdt and σdz in the SDE ensures that the stock price remains positive, reflecting the reality of financial markets. The geometric nature of the model differentiates it from a simple arithmetic random walk, aligning more closely with observed market behavior.
This SDE, although seemingly complex, provides a relatively straightforward yet powerful framework for modeling geometric brownian motion stock price. The parameters (μ, σ) can be estimated from historical stock price data. These estimates, along with a numerical method like the Euler-Maruyama method, allow for the simulation of numerous possible stock price paths, offering valuable insights into potential future price movements. The beauty of GBM lies in its ability to capture the essential characteristics of stock price dynamics while remaining computationally tractable. Analyzing simulated paths allows for comprehensive investigation into the behavior of geometric brownian motion stock price, making it an essential tool in financial modeling.
Interpreting the Parameters: Drift and Volatility
The drift and volatility parameters within the geometric Brownian motion stock price model are crucial for understanding the expected return and risk associated with a given stock. Drift represents the average rate of growth of the stock price over time. A positive drift indicates an expected upward trend, while a negative drift suggests a downward trend. Volatility, on the other hand, measures the standard deviation of the stock’s returns, quantifying the magnitude of its price fluctuations. High volatility implies significant price swings, reflecting a riskier investment. Low volatility suggests more stable price movements, indicating lower risk. The geometric Brownian motion stock price model uses these parameters to simulate realistic price paths.
Consider two companies: a well-established pharmaceutical company and a newly listed technology startup. The pharmaceutical company, with its stable revenue streams and established market position, might exhibit a relatively low volatility and a moderate positive drift. Its geometric Brownian motion stock price simulation would show relatively smooth upward movement. In contrast, the technology startup, operating in a highly competitive and rapidly changing market, is likely to display a higher volatility. Its geometric Brownian motion stock price may fluctuate more wildly, with periods of rapid growth and sharp declines. While the startup might have a higher expected growth (higher drift) to compensate for the increased risk, the uncertainty is significantly higher. Understanding these parameter differences is essential for making informed investment decisions using geometric Brownian motion stock price analysis. The geometric Brownian motion stock price model facilitates this understanding through simulation.
Different industries and individual companies will exhibit distinct drift and volatility values. Factors such as economic conditions, industry trends, company performance, and investor sentiment all influence these parameters. Analyzing historical stock price data can help estimate these values for specific assets. However, it’s critical to remember that these are estimates, and future performance may differ significantly. The geometric Brownian motion stock price model, while providing a valuable framework, cannot perfectly predict future price movements. Nonetheless, understanding how drift and volatility impact the geometric Brownian motion stock price is paramount for risk assessment and investment strategy development. The geometric Brownian motion stock price model helps visualize and quantify these crucial aspects of the market.
How to Simulate Stock Prices Using Geometric Brownian Motion
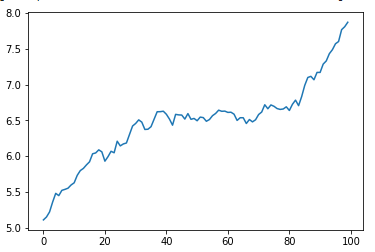
Simulating stock price paths using geometric Brownian motion (GBM) offers valuable insights into the potential future behavior of assets. The Euler-Maruyama method provides a straightforward approach to this simulation. This method approximates the solution of the stochastic differential equation that defines geometric brownian motion stock price movements. It relies on small time steps to iteratively update the price based on the drift and volatility parameters.
The process begins with an initial stock price, S0, and pre-defined parameters: the drift (μ), volatility (σ), and time step (Δt). The Euler-Maruyama method then employs the following iterative equation to generate a series of simulated prices: St+Δt = St * exp((μ – 0.5σ2)Δt + σ√ΔtZt). Here, Zt represents a random draw from a standard normal distribution (mean 0, variance 1), representing the randomness inherent in geometric brownian motion stock price fluctuations. The exponential term ensures that simulated prices remain positive, reflecting the nature of stock prices. Smaller time steps (Δt) lead to more accurate simulations, albeit requiring more computational power. The simulation generates multiple paths, each representing a possible evolution of the geometric brownian motion stock price.
Python’s NumPy library provides the tools for efficient implementation. The following code snippet demonstrates simulating 100 paths of a geometric brownian motion stock price over 252 trading days (approximately one year). This example uses a drift of 0.1 (10% annual return), a volatility of 0.2 (20% annual volatility), and an initial price of 100. Remember that this is a simplified model, and actual stock prices are far more complex. Nevertheless, simulating geometric brownian motion stock price provides a valuable tool for understanding risk and return in financial markets. The geometric brownian motion stock price simulation allows for exploring various ‘what-if’ scenarios under different parameterizations. It helps in assessing the sensitivity of outcomes to changes in drift and volatility. This is crucial for understanding potential risks and rewards associated with different investment strategies.
“`python
import numpy as np
import matplotlib.pyplot as plt
S0 = 100 # Initial stock price
mu = 0.1 # Drift
sigma = 0.2 # Volatility
dt = 1/252 # Time step (daily)
T = 1 # Time horizon (1 year)
n_paths = 100 # Number of paths to simulate
t = np.linspace(0,T,int(T/dt)+1)
Z = np.random.normal(size=(len(t)-1, n_paths))
S = np.zeros((len(t), n_paths))
S[0] = S0
for i in range(len(t)-1):
S[i+1] = S[i] * np.exp((mu – 0.5 * sigma**2) * dt + sigma * np.sqrt(dt) * Z[i])
plt.plot(t,S)
plt.xlabel(‘Time’)
plt.ylabel(‘Stock Price’)
plt.title(‘Geometric Brownian Motion Stock Price Simulation’)
plt.show()
“`
Applying Geometric Brownian Motion in Option Pricing Models
Geometric Brownian motion (GBM) serves as a cornerstone of numerous option pricing models. Its stochastic nature accurately reflects the unpredictable fluctuations inherent in geometric brownian motion stock price movements. This makes it ideally suited for modeling the underlying asset’s price evolution over time, a crucial factor in determining option values.
The Black-Scholes model, a landmark achievement in financial mathematics, explicitly relies on the assumption that the underlying asset price follows a GBM process. This model provides a closed-form solution for European-style options, enabling efficient calculation of theoretical option prices. The geometric brownian motion stock price path simulations, as demonstrated previously, directly inform the inputs needed for the Black-Scholes formula. Simulating numerous price paths allows for a more comprehensive understanding of potential option payoffs and associated risks. The accuracy of the Black-Scholes option price depends significantly on the validity of the GBM assumption for the underlying geometric brownian motion stock price.
Beyond the Black-Scholes model, GBM finds application in various other option pricing frameworks. These models often extend or modify the basic GBM assumptions to account for factors like dividends, early exercise features (American options), or stochastic volatility. However, the foundation of many sophisticated option pricing approaches still rests on the core principles of GBM, making it an indispensable tool in quantitative finance. The ability to simulate geometric brownian motion stock price trajectories using GBM empowers practitioners to assess the impact of various market scenarios on option pricing and hedging strategies.
Limitations and Extensions of Geometric Brownian Motion
While geometric Brownian motion (GBM) serves as a cornerstone model for stock price dynamics, it possesses inherent limitations. The assumption of constant volatility, a key parameter in the geometric brownian motion stock price model, often fails to reflect real-world market behavior. Stock price volatility tends to fluctuate, clustering periods of high volatility with periods of low volatility. This phenomenon, known as stochastic volatility, is not captured by standard GBM. Furthermore, GBM assumes continuous price changes, neglecting the impact of sudden, significant price jumps often caused by unexpected news or events. These jumps can drastically alter the geometric brownian motion stock price trajectory, deviating significantly from the smooth paths predicted by the model.
Another limitation is the distribution of returns implied by GBM. The model predicts a normal distribution of log returns. However, empirical studies frequently show that stock returns exhibit “fat tails,” meaning extreme events (large positive or negative returns) occur more frequently than predicted by a normal distribution. This deviation from normality impacts the accuracy of risk assessments and option pricing models based on GBM. The assumption of constant drift, representing the average rate of return, is also an oversimplification. In reality, the expected return of a stock can change over time due to various economic and market factors. The geometric brownian motion stock price model’s inability to account for these dynamic changes limits its predictive power, especially over longer horizons.
To address these shortcomings, researchers have developed more sophisticated models. Jump diffusion models, for example, incorporate random jumps into the GBM framework, allowing for sudden price discontinuities. Stochastic volatility models allow volatility itself to follow a stochastic process, capturing the time-varying nature of market risk. These extensions strive to provide a more realistic and nuanced representation of geometric brownian motion stock price movements, enhancing the accuracy of financial modeling and risk management applications. However, it’s crucial to remember that even these extended models are approximations of complex market realities. The choice of model depends heavily on the specific application and the level of detail required.
Real-World Applications Beyond Option Pricing
Geometric Brownian motion (GBM) extends far beyond option pricing. Its ability to model the stochastic behavior of asset prices makes it invaluable in portfolio optimization. By simulating numerous geometric brownian motion stock price paths, analysts can assess the potential range of portfolio returns under various market conditions. This allows for more informed decisions regarding asset allocation and risk management. This application leverages the GBM model’s capacity to capture the inherent uncertainty in financial markets, leading to more robust investment strategies.
Risk management professionals also utilize geometric brownian motion stock price models extensively. Value at Risk (VaR) calculations, for example, frequently rely on GBM simulations to estimate potential losses under adverse market scenarios. By inputting different volatility parameters, reflecting different market conditions, these models provide a range of potential losses, allowing firms to set aside adequate capital reserves. The ability to model tail risk, even though GBM simplifies some aspects of market behavior, offers critical insights for managing financial risk effectively. Accurate estimations using GBM are crucial to the overall stability of financial institutions.
Furthermore, GBM finds applications in areas such as derivative pricing beyond options. Models for other derivative securities often incorporate GBM to capture the underlying asset’s price fluctuations. Similarly, in areas like real estate and commodities markets, GBM provides a suitable framework for modeling price dynamics, though adjustments might be needed to account for specific market characteristics. The versatility of GBM, its relative simplicity, and its ability to capture fundamental aspects of price movements make geometric brownian motion stock price modeling a powerful tool across diverse financial applications.
Conclusion: GBM as a Powerful Tool in Financial Modeling
This exploration of geometric Brownian motion stock price modeling reveals its significant role in financial analysis. The model’s simplicity, coupled with its ability to capture the inherent randomness of stock prices, makes it a valuable tool. Understanding the drift and volatility parameters allows for estimations of expected returns and risk, informing investment decisions. The Euler-Maruyama method provides a practical approach to simulate stock price paths, facilitating applications such as option pricing. The geometric Brownian motion framework, while foundational, provides a robust starting point for understanding asset price dynamics.
Its application extends beyond option pricing. Portfolio optimization and risk management strategies leverage the insights offered by geometric Brownian motion. However, it’s crucial to acknowledge the limitations. Real-world markets exhibit complexities like jumps and stochastic volatility, which the basic GBM model cannot fully capture. This necessitates the exploration of more advanced models to account for these market nuances. Geometric Brownian motion serves as a cornerstone, providing a strong theoretical foundation for further study in quantitative finance.
The elegance and practicality of geometric Brownian motion in stock price modeling are undeniable. While limitations exist, its ability to simulate and predict stock price behavior remains a powerful tool for financial professionals. Further research into its extensions and alternative models is encouraged for a deeper understanding of market dynamics. Mastering geometric Brownian motion provides a solid foundation for navigating the complexities of financial markets.