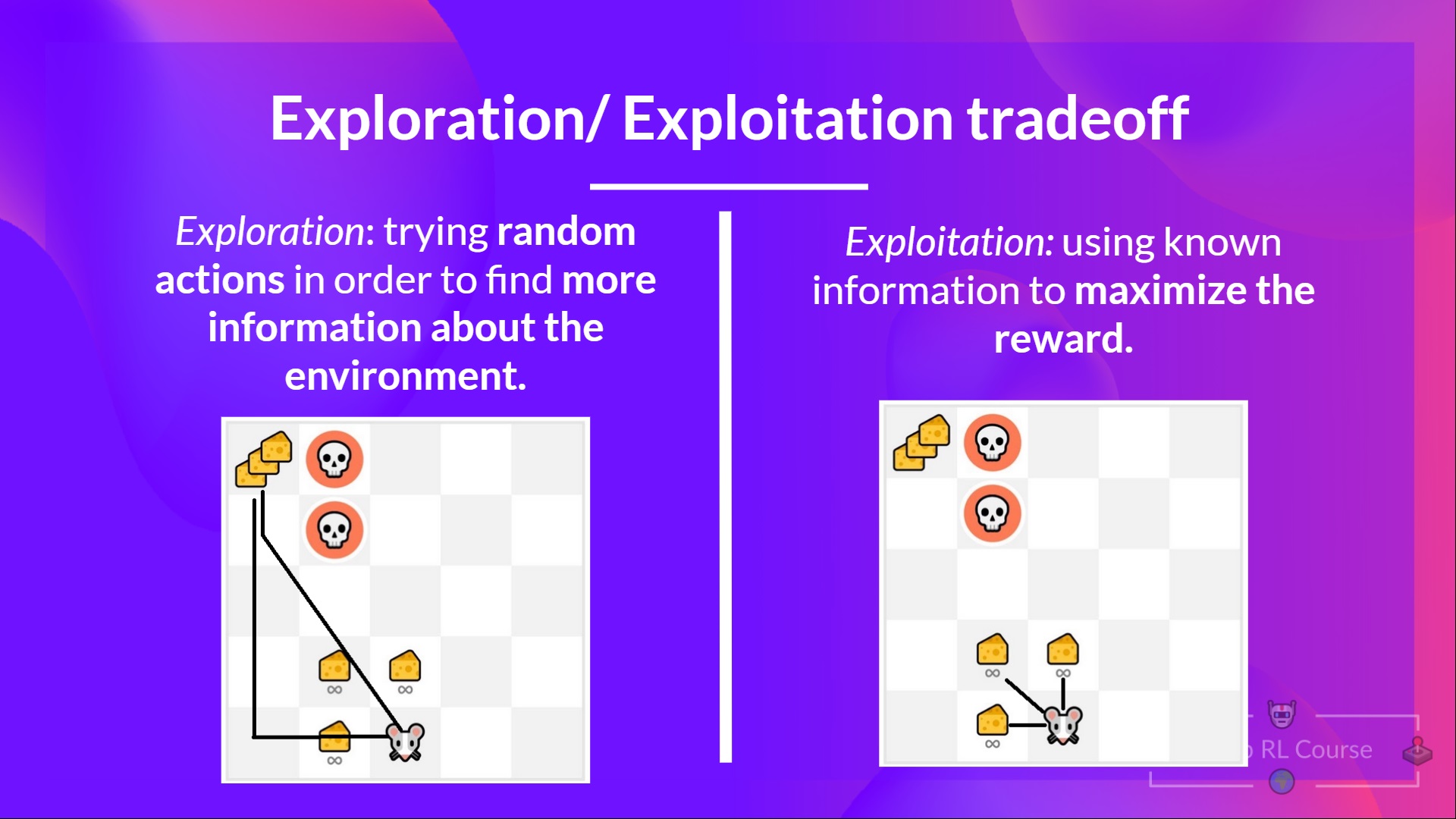
The Role of Exploration and Exploitation in Deep Reinforcement Learning
In the field of deep reinforcement learning, the epsilon-greedy strategy plays a crucial role in balancing exploration and exploitation. Exploration refers to the process of trying out new actions to gather information about the environment, while exploitation involves choosing the action that currently appears to be the best based on the available information. The epsilon-greedy strategy helps agents to make this trade-off by selecting random actions with a probability of epsilon, and the action with the highest expected reward with a probability of 1-epsilon. This approach ensures that the agent continues to explore the environment, while also taking advantage of its current knowledge to make informed decisions. By maintaining a balance between exploration and exploitation, the epsilon-greedy strategy enables deep reinforcement learning algorithms to converge to optimal policies more efficiently.
Understanding the Epsilon-Greedy Strategy: Key Principles and Implementation
The epsilon-greedy strategy is a popular exploration technique used in deep reinforcement learning to balance the trade-off between exploration and exploitation. At its core, the epsilon-greedy strategy involves selecting the action with the highest expected reward with a probability of 1-epsilon, and selecting a random action with a probability of epsilon. This approach ensures that the agent continues to explore the environment, while also taking advantage of its current knowledge to make informed decisions. The key principle behind the epsilon-greedy strategy is to maintain a balance between exploration and exploitation. By selecting random actions with a probability of epsilon, the agent is able to gather new information about the environment and avoid getting stuck in local optima. At the same time, by selecting the action with the highest expected reward with a probability of 1-epsilon, the agent is able to make progress towards its goal and converge to an optimal policy more efficiently.
Implementing the epsilon-greedy strategy in deep reinforcement learning algorithms is relatively straightforward. At each time step, the agent generates a random number between 0 and 1. If the random number is less than epsilon, the agent selects a random action. Otherwise, the agent selects the action with the highest expected reward. The value of epsilon can be set manually or adapted dynamically over time based on the agent’s current knowledge and performance.
It is important to note that the epsilon-greedy strategy is just one of many exploration techniques used in deep reinforcement learning. While it is a simple and effective approach, it may not be the best choice for all scenarios. Other exploration techniques, such as Boltzmann exploration and UCB1, may be more suitable for certain types of problems or environments. It is therefore important to carefully consider the strengths and weaknesses of each approach when designing deep reinforcement learning algorithms.
How to Implement the Epsilon-Greedy Strategy in Deep Reinforcement Learning
Implementing the epsilon-greedy strategy in deep reinforcement learning involves a few key steps. Here is a step-by-step guide to help you get started:
Define the exploration rate: The exploration rate, or epsilon, determines how often the agent will explore new actions versus exploiting known ones. A higher exploration rate means the agent will explore more often, while a lower exploration rate means the agent will exploit known actions more often.
Choose the action: At each time step, the agent will choose an action based on the exploration rate. With a probability of 1 – epsilon, the agent will choose the action with the highest expected reward. With a probability of epsilon, the agent will choose a random action.
Update the expected rewards: After the agent takes an action and receives a reward, it will update the expected rewards for each action based on the new information.
Decrease the exploration rate: Over time, the exploration rate should be decreased to allow the agent to exploit known actions more often. This can be done using a decay schedule, where the exploration rate is gradually reduced over time.
Here is an example of how to implement the epsilon-greedy strategy in Python using the TensorFlow library:
import tensorflow as tf # Define the exploration rate epsilon = 0.1 # Define the number of actions num\_actions = 3 # Define the expected rewards for each action expected\_rewards = tf.Variable(tf.zeros(num\_actions)) # Define the function to choose an action def choose\_action(): # With probability 1 - epsilon, choose the action with the highest expected reward if tf.random.uniform([], maxval=1) > epsilon: return tf.argmax(expected\_rewards) # With probability epsilon, choose a random action else: return tf.random.uniform([], maxval=num\_actions, dtype=tf.int32) # Define the function to update the expected rewards def update\_expected\_rewards(action, reward): # Update the expected reward for the chosen action expected\_rewards[action].assign(expected\_rewards[action] + (reward - expected\_rewards[action]) / 10.0) In this example, the epsilon variable defines the exploration rate, and the num_actions variable defines the number of actions available to the agent. The expected_rewards variable stores the expected rewards for each action, and the choose_action function selects an action based on the exploration rate. The update_expected_rewards function updates the expected rewards based on the new information.
When implementing the epsilon-greedy strategy in deep reinforcement learning, it is important to choose the right value for epsilon and to decrease it over time using a decay schedule. A good starting point for epsilon is 1.0, which means the agent will explore new actions at every time step. Over time, the exploration rate should be gradually decreased to allow the agent to exploit known actions more often. A common decay schedule is to decrease epsilon by a factor of 0.99 at each time step.
In addition to the basic implementation of the epsilon-greedy strategy, there are several advanced topics to consider, such as decay schedules, adaptive epsilon, and epsilon-greedy with experience replay. These topics can help improve the performance of the epsilon-greedy strategy in deep reinforcement learning.
Comparing the Epsilon-Greedy Strategy with Other Exploration Techniques
While the epsilon-greedy strategy is a popular and effective exploration technique in deep reinforcement learning, it is not the only approach. In this section, we will compare the epsilon-greedy strategy with other exploration techniques, such as Boltzmann exploration and UCB1, to help you determine which approach is best for your specific use case.
Boltzmann Exploration
Boltzmann exploration, also known as softmax exploration, is a probabilistic exploration technique that involves selecting actions based on a temperature-based distribution. Specifically, the probability of selecting an action is proportional to its expected reward raised to the power of the inverse temperature. As the temperature decreases, the distribution becomes more peaked, and the agent becomes more exploitative. Conversely, as the temperature increases, the distribution becomes more uniform, and the agent becomes more explorative.
Compared to the epsilon-greedy strategy, Boltzmann exploration provides a smoother transition between exploration and exploitation, as the probability of selecting suboptimal actions decreases gradually rather than abruptly. However, Boltzmann exploration can be computationally expensive, as it requires computing the expected rewards for all actions at each time step. Additionally, choosing the right temperature value can be challenging, as a temperature that is too high or too low can result in suboptimal performance.
UCB1
UCB1, or Upper Confidence Bound 1, is an exploration technique that involves selecting actions based on a confidence interval around the expected reward. Specifically, the UCB1 formula is given by:
A = argmaxa [Qa + c \* sqrt(log N/na)]
Where A is the action to select, Qa is the expected reward of action a, N is the total number of time steps, na is the number of times action a has been selected, and c is a constant that controls the exploration-exploitation trade-off.
Compared to the epsilon-greedy strategy, UCB1 provides a more principled approach to exploration, as it explicitly balances the exploitation of known actions with the exploration of uncertain
Tuning the Epsilon-Greedy Strategy for Optimal Performance
Choosing the right value for epsilon and determining when to decrease it over time are crucial for the success of the epsilon-greedy strategy in deep reinforcement learning. In this section, we will discuss how to tune the epsilon-greedy strategy for optimal performance.
Choosing the Right Value for Epsilon
The value of epsilon determines the balance between exploration and exploitation in the epsilon-greedy strategy. A high value of epsilon encourages more exploration, while a low value of epsilon encourages more exploitation. Choosing the right value for epsilon depends on the specific problem and the current state of the agent’s knowledge.
In general, a good starting point for epsilon is 1.0, which encourages complete exploration. As the agent gains more knowledge about the environment, epsilon can be gradually decreased to encourage more exploitation. A common approach is to use a decay schedule, where epsilon is decreased by a fixed amount at each time step or after a fixed number of steps.
Decreasing Epsilon Over Time
Decreasing epsilon over time is important for the epsilon-greedy strategy to converge to an optimal policy. A high value of epsilon for a prolonged period can result in the agent never exploiting the knowledge it has gained about the environment. On the other hand, decreasing epsilon too quickly can result in premature convergence to a suboptimal policy.
A common approach to decreasing epsilon over time is to use a decay schedule, where epsilon is multiplied by a fixed decay factor at each time step or after a fixed number of steps. For example, if the decay factor is 0.99, epsilon will be decreased by 1% at each time step. The decay factor can be adjusted based on the specific problem and the desired rate of convergence.
Practical Examples and Tips
Here are some practical examples and tips for tuning the epsilon-greedy strategy:
- Start with a high value of epsilon (e.g., 1.0) and gradually decrease it over time.
- Use a decay schedule to decrease epsilon at a fixed rate (e.g., multiply epsilon by a decay factor of 0.99 at each time step).
- Monitor the performance of the agent over time and adjust the value of epsilon as needed.
- Consider using a dynamic epsilon, where the value of epsilon is adjusted based on the current state of the agent’s knowledge (e.g., increase epsilon when the agent is in a new state and decrease it when the agent is in a familiar state).
- Experiment with different values of epsilon and decay factors to find the optimal balance between exploration and exploitation for the specific problem.
Tuning the epsilon-greedy strategy is an important aspect of deep reinforcement learning. By choosing the right value for epsilon and decreasing it over time, the agent can balance exploration and exploitation and converge to an optimal policy. With the right approach, the epsilon-greedy strategy can be a powerful tool for solving complex reinforcement learning problems.
Advanced Topics in Epsilon-Greedy Strategy for Deep Reinforcement Learning
In this section, we will explore advanced topics in the epsilon-greedy strategy for deep reinforcement learning, including decay schedules, adaptive epsilon, and epsilon-greedy with experience replay. These techniques can help improve the performance and efficiency of the epsilon-greedy strategy in complex reinforcement learning problems.
Decay Schedules
Decay schedules are a common technique used to adjust the value of epsilon over time. By gradually decreasing the value of epsilon, the agent can balance exploration and exploitation during the learning process. There are several types of decay schedules, including linear decay, exponential decay, and step decay.
- Linear decay: In linear decay, the value of epsilon decreases linearly over time. For example, if the initial value of epsilon is 1.0 and the decay rate is 0.001, the value of epsilon will be 0.999 after one time step, 0.998 after two time steps, and so on.
- Exponential decay: In exponential decay, the value of epsilon decreases exponentially over time. For example, if the initial value of epsilon is 1.0 and the decay rate is 0.99, the value of epsilon will be 0.99 after one time step, 0.9801 after two time steps, 0.970299 after three time steps, and so on.
- Step decay: In step decay, the value of epsilon decreases by a fixed amount after a fixed number of time steps. For example, if the initial value of epsilon is 1.0 and the decay rate is 0.1, the value of epsilon will be 0.9 after every 10 time steps.
Adaptive Epsilon
Adaptive epsilon is a technique that adjusts the value of epsilon based on the current state of the agent. By adapting the value of epsilon to the current state, the agent can balance exploration and exploitation more effectively. There are several ways to implement adaptive epsilon, including using a separate epsilon value for each state, using a function of the current reward to adjust the value of epsilon, and using a neural network to predict the value of epsilon based on the current state.
Epsilon-Greedy with Experience Replay
Experience replay is a technique used in deep reinforcement learning to improve the efficiency of the learning process. By storing past experiences in a buffer and replaying them during training, the agent can learn from a larger and more diverse set of experiences. Epsilon-greedy with experience replay is a technique that combines epsilon-greedy exploration with experience replay. By using epsilon-greedy exploration during the collection of experiences and experience replay during training, the agent can balance exploration and exploitation more effectively.
In summary, decay schedules, adaptive epsilon, and epsilon-greedy with experience replay are advanced topics in the epsilon-greedy strategy for deep reinforcement learning. By incorporating these techniques, the agent can balance exploration and exploitation more effectively and improve the performance and efficiency of the learning process. As deep reinforcement learning continues to evolve, there are many open research questions and opportunities for innovation in the epsilon-greedy strategy and other exploration techniques.
Real-World Applications of the Epsilon-Greedy Strategy in Deep Reinforcement Learning
The epsilon-greedy strategy has been widely used in deep reinforcement learning applications, particularly in areas where there is a need for efficient exploration and exploitation. Here are some examples of real-world applications of the epsilon-greedy strategy in deep reinforcement learning:
Robotics
In robotics, the epsilon-greedy strategy is used to enable robots to learn how to perform tasks by exploring their environment and exploiting the knowledge they gain. For example, a robot arm can use the epsilon-greedy strategy to learn how to pick up and move objects by exploring different movements and selecting the ones that result in successful outcomes. This approach has been used in applications such as assembly line automation, where robots need to learn how to perform complex tasks efficiently.
Gaming
The epsilon-greedy strategy has been used in game development to create intelligent non-player characters (NPCs) that can learn how to play games by exploring the game environment and exploiting the knowledge they gain. For example, in a racing game, the epsilon-greedy strategy can be used to enable NPCs to learn how to drive by exploring different driving techniques and selecting the ones that result in faster times. This approach has been used in applications such as creating realistic NPCs in open-world games, where NPCs need to learn how to navigate complex environments and interact with other characters.
Autonomous Systems
The epsilon-greedy strategy is also used in autonomous systems, such as self-driving cars, to enable the system to learn how to navigate complex environments by exploring different routes and selecting the ones that result in safe and efficient travel. For example, a self-driving car can use the epsilon-greedy strategy to learn how to navigate busy intersections by exploring different paths and selecting the ones that result in safe and efficient travel. This approach has been used in applications such as ride-sharing services, where self-driving cars need to learn how to navigate complex urban environments efficiently.
In summary, the epsilon-greedy strategy has been widely used in deep reinforcement learning applications, particularly in areas where there is a need for efficient exploration and exploitation. By using the epsilon-greedy strategy, robots, NPCs, and autonomous systems can learn how to perform tasks by exploring their environment and exploiting the knowledge they gain. As deep reinforcement learning continues to evolve, there are many opportunities for innovation in the application of the epsilon-greedy strategy and other exploration techniques in real-world scenarios.
Future Directions and Open Research Questions in Epsilon-Greedy Strategy for Deep Reinforcement Learning
The epsilon-greedy strategy has been a foundational exploration technique in deep reinforcement learning, but there are still many open research questions and opportunities for innovation in this area. Here are some future directions and open research questions in the epsilon-greedy strategy for deep reinforcement learning:
Trade-off between Exploration and Exploitation
One of the key challenges in reinforcement learning is balancing exploration and exploitation. The epsilon-greedy strategy provides a simple and effective way to balance these two aspects, but there is still much to be learned about the optimal balance between exploration and exploitation in different scenarios. Future research could explore how to dynamically adjust the value of epsilon based on the current state of the learning process, or how to incorporate other exploration techniques to improve the balance between exploration and exploitation.
Role of Contextual Information
Contextual information, such as the current state of the environment or the history of past actions, can be used to improve the performance of the epsilon-greedy strategy. Future research could explore how to incorporate contextual information into the epsilon-greedy strategy to improve its performance in complex environments. For example, contextual information could be used to adjust the value of epsilon based on the current state of the environment, or to select the best action based on the history of past actions.
Potential for Hybrid Approaches
Hybrid approaches that combine the epsilon-greedy strategy with other exploration techniques, such as Thompson sampling or UCB1, could provide improved performance in certain scenarios. Future research could explore how to combine the epsilon-greedy strategy with other exploration techniques to improve its performance in complex environments. For example, a hybrid approach could use the epsilon-greedy strategy for initial exploration, and then switch to Thompson sampling or UCB1 for fine-tuning the learning process.
In summary, the epsilon-greedy strategy has been a foundational exploration technique in deep reinforcement learning, but there are still many open research questions and opportunities for innovation in this area. By exploring the trade-off between exploration and exploitation, the role of contextual information, and the potential for hybrid approaches, researchers can continue to push the boundaries of what is possible with the epsilon-greedy strategy in deep reinforcement learning. As deep reinforcement learning continues to evolve, there are many exciting opportunities for innovation and discovery in this field.