Understanding Deep Deterministic Policy Gradient (DDPG) Algorithms
Reinforcement learning (RL) is a significant branch of artificial intelligence (AI) that focuses on training agents to make decisions and take actions in complex environments to maximize cumulative rewards. Among the various RL techniques, Deep Deterministic Policy Gradient (DDPG) algorithms have emerged as a powerful approach for addressing continuous action spaces. DDPG algorithms are a type of actor-critic method that combines the benefits of Q-learning and policy gradients. They employ two neural networks—an actor network and a critic network—to learn the optimal policy and value function, respectively. The actor network is responsible for selecting actions, while the critic network evaluates the chosen actions and provides feedback to the actor network for improvement.
The primary advantage of DDPG algorithms is their ability to handle continuous action spaces, which is particularly useful in robotics, autonomous driving, and resource management. Unlike traditional RL methods that struggle with continuous action spaces, DDPG algorithms can smoothly explore and exploit the environment, leading to more efficient and effective learning.
Moreover, DDPG algorithms employ a replay buffer to store and reuse past experiences, further enhancing their learning efficiency. By sampling from the replay buffer, DDPG algorithms can break the correlation between consecutive samples, ensuring stable and robust learning.
In summary, DDPG algorithms are a valuable addition to the reinforcement learning toolbox, offering a robust and efficient solution for addressing continuous action spaces. By combining the strengths of Q-learning and policy gradients, DDPG algorithms have demonstrated their potential in various real-world applications, making them an essential topic for AI researchers and practitioners alike.
Key Components of DDPG Algorithms
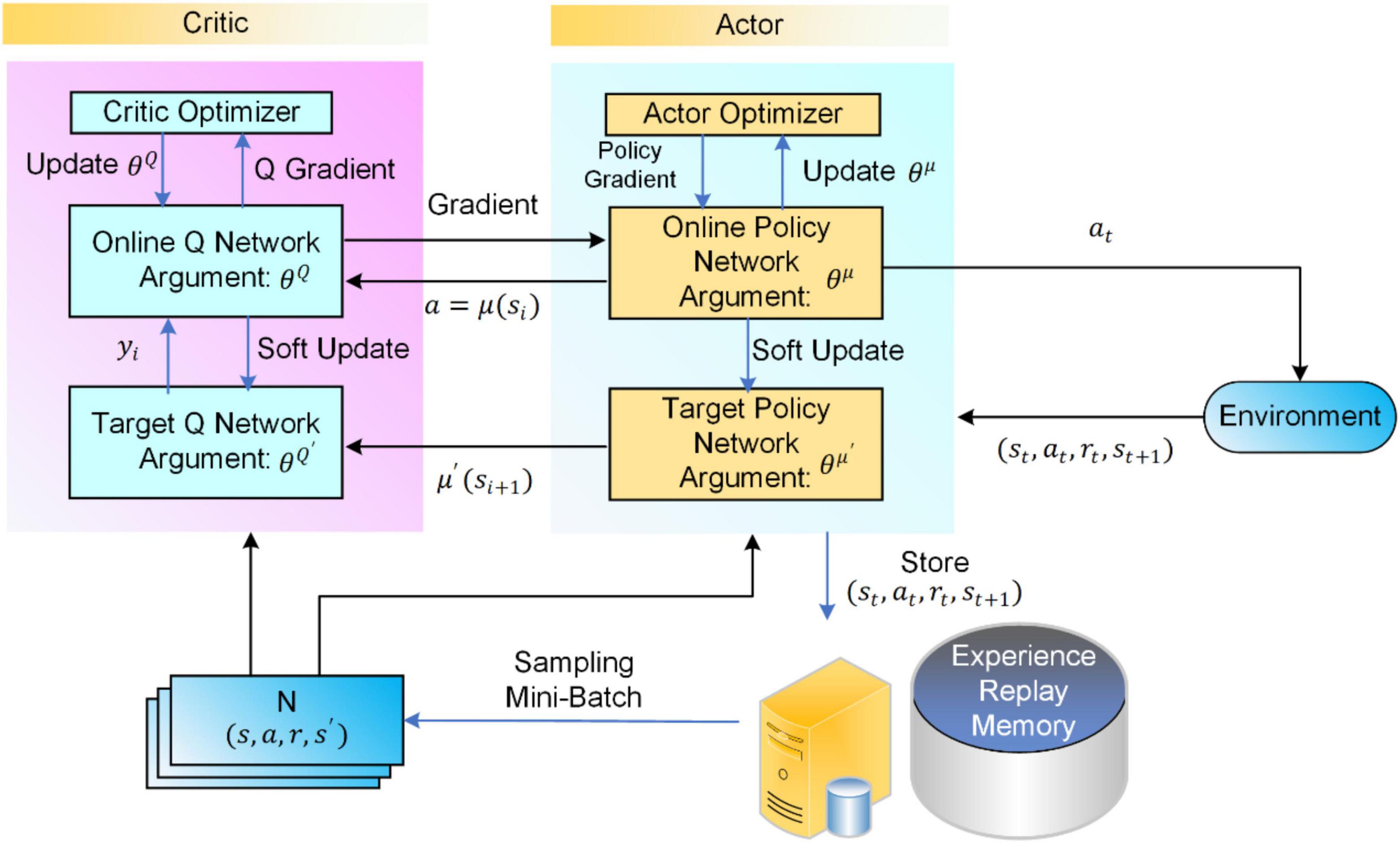
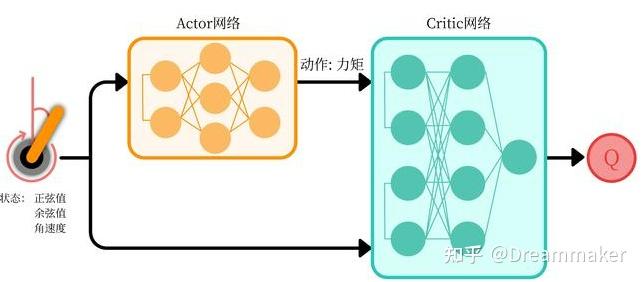
DDPG algorithms consist of three main components: the actor network, the critic network, and the replay buffer. These elements work together to optimize policy functions and enable efficient learning in continuous action spaces.
Actor Network
The actor network is a neural network that takes the current state of the environment as input and outputs a continuous action. The actor network is responsible for selecting actions that maximize the expected cumulative reward. During the training process, the actor network’s parameters are updated using the policy gradient method, which adjusts the parameters in the direction that increases the expected return.
Critic Network
The critic network is another neural network that estimates the action-value function (Q-value) for a given state-action pair. The critic network takes the current state and the action output from the actor network as inputs and outputs the estimated Q-value. The critic network’s parameters are updated using the temporal-difference (TD) error, which measures the difference between the estimated Q-value and the actual Q-value. By minimizing the TD error, the critic network provides feedback to the actor network, enabling it to select better actions.
Replay Buffer
The replay buffer is a data structure that stores past experiences (state, action, reward, next state) encountered during the training process. By sampling from the replay buffer, DDPG algorithms can break the correlation between consecutive samples, ensuring stable and robust learning. The replay buffer also allows for the efficient use of experiences, as samples can be reused multiple times during training.
Interaction between Components
During the training process, the actor network and the critic network interact as follows:
The actor network selects an action based on the current state.
The environment executes the action and returns the next state and the reward.
The critic network estimates the Q-value for the current state-action pair.
The TD error is calculated, and the critic network’s parameters are updated.
The policy gradient is calculated, and the actor network’s parameters are updated.
This interaction enables the DDPG algorithm to learn the optimal policy and value function for continuous action spaces, making it an effective solution for various real-world applications.
Implementing Deep Deterministic Policy Gradient (DDPG) Algorithms: A Step-by-Step Guide
Deep Deterministic Policy Gradient (DDPG) algorithms are a powerful reinforcement learning technique for optimizing policy functions in continuous action spaces. Implementing DDPG algorithms involves setting up the environment, initializing the networks, and executing the training loop. This section provides a clear, detailed guide on implementing DDPG algorithms, using a simple example to illustrate the process.
Step 1: Setting Up the Environment
The first step in implementing DDPG algorithms is to set up the environment. This involves defining the problem, selecting a suitable simulation, and specifying the state and action spaces. For instance, consider a simple environment where an agent controls a car in a one-dimensional world. The state space could be the car’s current position and velocity, while the action space would be the force applied to the car.
Step 2: Initializing the Networks
Once the environment is set up, the next step is to initialize the actor and critic networks. Both networks are typically multi-layer perceptrons (MLPs) with the actor network outputting continuous actions and the critic network estimating the Q-value. Initialize the networks with random weights and biases, and define the input and output dimensions based on the state and action spaces.
Step 3: Defining the Replay Buffer
The replay buffer is a data structure that stores past experiences (state, action, reward, next state) encountered during the training process. Implement a replay buffer with a fixed capacity, and define methods for adding and sampling experiences. This enables the DDPG algorithm to break the correlation between consecutive samples and efficiently use experiences during training.
Step 4: Executing the Training Loop
The training loop is the core of the DDPG algorithm, where the actor and critic networks are updated based on the observed experiences. The loop consists of the following steps:
- Collect experiences by having the agent interact with the environment using the current policy.
- Store the experiences in the replay buffer.
- Sample a batch of experiences from the replay buffer.
- Calculate the target Q-value for each experience using the Bellman equation.
- Calculate the TD error between the estimated and target Q-values.
- Update the critic network’s parameters using gradient descent and the TD error.
- Calculate the policy gradient for the actor network.
- Update the actor network’s parameters using the policy gradient.
Repeat steps 1-8 for a fixed number of episodes or until convergence. Periodically update the target networks with the current networks’ parameters to stabilize learning.
Example: Implementing DDPG for CartPole
To illustrate the implementation process, consider the classic CartPole environment from the OpenAI Gym library. The environment consists of a pole attached to a cart, which moves along a one-dimensional track. The goal is to balance the pole upright for as long as possible by applying forces to the cart.
Implementing DDPG for CartPole involves setting up the environment, initializing the networks, and executing the training loop. The state space consists of the cart’s position and velocity, as well as the pole’s angle and angular velocity. The action space is a continuous value representing the force applied to the cart. By following the steps outlined above, you can successfully implement DDPG algorithms for the CartPole environment.
How to Troubleshoot Common Issues in Deep Deterministic Policy Gradient (DDPG) Algorithms
Deep Deterministic Policy Gradient (DDPG) algorithms are a powerful reinforcement learning technique for optimizing policy functions in continuous action spaces. However, implementing DDPG algorithms can be challenging, with issues such as convergence problems, instability, and high variance. This section identifies common challenges and suggests potential solutions and best practices to overcome these problems.
Convergence Issues
DDPG algorithms may struggle to converge, especially when dealing with complex environments. To address convergence issues, consider the following:
- Ensure that the hyperparameters, such as learning rates, discount factors, and network architectures, are appropriately set.
- Implement early stopping techniques to prevent overfitting and improve convergence.
- Monitor the training process and adjust the learning rate or other hyperparameters as needed.
Instability
DDPG algorithms can be unstable, with oscillating or diverging performance. To improve stability, consider the following:
- Implement target networks with periodic updates to stabilize learning.
- Use techniques such as batch normalization and weight regularization to reduce overfitting and improve stability.
- Gradually increase the exploration rate and anneal it over time to ensure a smooth transition from exploration to exploitation.
High Variance
DDPG algorithms can suffer from high variance, leading to unpredictable performance. To reduce variance, consider the following:
- Increase the replay buffer size to ensure a more diverse set of experiences.
- Use a higher batch size during training to reduce the impact of individual experiences.
- Implement techniques such as gradient clipping and adaptive learning rates to control the impact of large gradients.
By following these best practices and addressing common challenges, you can improve the performance and reliability of DDPG algorithms in various applications.

Applications of Deep Deterministic Policy Gradient (DDPG) Algorithms in Real-World Scenarios
Deep Deterministic Policy Gradient (DDPG) algorithms have emerged as a powerful reinforcement learning technique for continuous action spaces, offering significant potential for real-world applications. This section discusses various applications of DDPG algorithms, including robotics, autonomous driving, and resource management.
Robotics
DDPG algorithms can be applied to robotic systems to optimize motion planning, manipulation, and control. For instance, researchers have used DDPG algorithms to train robotic arms for complex tasks such as grasping and manipulation. By learning from interactions with the environment, DDPG algorithms enable robots to adapt and improve their performance over time.
Autonomous Driving
DDPG algorithms can be used in autonomous driving systems to optimize vehicle control and decision-making. For example, DDPG algorithms can be employed to manage acceleration, braking, and steering, ensuring safe and efficient driving. By learning from real-world driving scenarios, DDPG algorithms can help autonomous vehicles adapt to various road conditions and traffic situations.
Resource Management
DDPG algorithms can be applied to resource management problems, such as optimizing energy consumption, scheduling tasks, and managing infrastructure. For instance, DDPG algorithms can be used to optimize the allocation of computing resources in data centers, ensuring efficient use of resources and minimizing energy consumption. By learning from historical data and real-time feedback, DDPG algorithms can help improve resource management and reduce costs.
These examples demonstrate the potential of DDPG algorithms in various real-world scenarios. By optimizing policy functions in continuous action spaces, DDPG algorithms can help solve complex problems and drive innovation in various industries.
Comparing Deep Deterministic Policy Gradient (DDPG) Algorithms with Other Reinforcement Learning Methods
Deep Deterministic Policy Gradient (DDPG) algorithms are a powerful reinforcement learning technique for continuous action spaces. However, they are not the only option available. In this section, we compare DDPG algorithms with other reinforcement learning methods, such as Q-learning, Deep Q-Networks (DQN), and Proximal Policy Optimization (PPO). By understanding the strengths and weaknesses of each method, we can make informed decisions about which approach to use in different scenarios.
Q-Learning vs. DDPG Algorithms
Q-learning is a popular reinforcement learning method for discrete action spaces. However, it is not well-suited for continuous action spaces. DDPG algorithms, on the other hand, are specifically designed for continuous action spaces. While Q-learning can be extended to continuous action spaces using techniques such as Deep Deterministic Policy Gradient (DDPG) algorithms, these methods are generally more complex and computationally expensive than DDPG algorithms.
Deep Q-Networks (DQN) vs. DDPG Algorithms
Deep Q-Networks (DQN) are a popular reinforcement learning method for discrete action spaces. Like Q-learning, DQN can be extended to continuous action spaces using techniques such as DDPG algorithms. However, DDPG algorithms are generally more efficient and effective than DQN in continuous action spaces. This is because DDPG algorithms use an actor-critic architecture, which allows them to learn a policy function directly, while DQN uses a value function to estimate the optimal action.
Proximal Policy Optimization (PPO) vs. DDPG Algorithms
Proximal Policy Optimization (PPO) is a popular reinforcement learning method for discrete and continuous action spaces. PPO is a policy gradient method, which means it learns a policy function directly. While PPO is generally more efficient and effective than DDPG algorithms in discrete action spaces, DDPG algorithms can be more efficient and effective in continuous action spaces. This is because DDPG algorithms use an actor-critic architecture, which allows them to learn a policy function directly, while PPO uses a surrogate objective function to update the policy.
In summary, DDPG algorithms are a powerful reinforcement learning technique for continuous action spaces. While other reinforcement learning methods, such as Q-learning, Deep Q-Networks (DQN), and Proximal Policy Optimization (PPO), can be extended to continuous action spaces, DDPG algorithms are generally more efficient and effective in these scenarios. By understanding the strengths and weaknesses of each method, we can make informed decisions about which approach to use in different scenarios.
Emerging Trends and Future Directions in DDPG Research
Deep Deterministic Policy Gradient (DDPG) algorithms have been a significant breakthrough in reinforcement learning, particularly for continuous control tasks. As research in this field continues to evolve, several emerging trends and future directions are shaping the landscape of DDPG research. In this section, we will explore some of these trends, including multi-agent DDPG, hierarchical DDPG, and continuous control with DDPG.
Multi-Agent DDPG
Multi-agent systems are becoming increasingly prevalent in various applications, such as autonomous vehicles, robotics, and smart grids. Multi-agent DDPG algorithms are a natural extension of traditional DDPG algorithms, where multiple agents learn to interact with each other and their environment to achieve a common goal. Multi-agent DDPG algorithms face unique challenges, such as non-stationarity, communication, and coordination. Recent research has focused on addressing these challenges by developing decentralized and centralized multi-agent DDPG algorithms, incorporating communication protocols, and using graph neural networks to model the relationships between agents.
Hierarchical DDPG
Hierarchical reinforcement learning (HRL) is a framework that decomposes complex tasks into a hierarchy of subtasks. Hierarchical DDPG algorithms are a promising approach for addressing the challenges of scalability and generalization in reinforcement learning. Recent research has focused on developing hierarchical DDPG algorithms that can learn a hierarchy of skills and options, transfer learning across tasks, and adapt to changing environments. These algorithms have shown promising results in various applications, such as robotics, game playing, and autonomous driving.
Continuous Control with DDPG
Continuous control tasks are prevalent in various applications, such as robotics, autonomous driving, and resource management. DDPG algorithms have been successful in addressing continuous control tasks, but there are still several challenges to overcome, such as exploration, stability, and sample efficiency. Recent research has focused on addressing these challenges by developing exploration strategies, using off-policy data, and incorporating prior knowledge. These advances have led to significant improvements in the performance and efficiency of DDPG algorithms in continuous control tasks.
In summary, multi-agent DDPG, hierarchical DDPG, and continuous control with DDPG are some of the emerging trends and future directions in DDPG research. These trends are shaping the landscape of reinforcement learning and have the potential to address some of the challenges of scalability, generalization, and complexity in various applications. As research in this field continues to evolve, we can expect to see even more innovative and creative concepts that provide value and usefulness to the reader.
Conclusion: The Role and Impact of DDPG Algorithms in AI
Deep Deterministic Policy Gradient (DDPG) algorithms have emerged as a powerful and versatile tool in reinforcement learning, enabling artificial intelligence (AI) systems to solve complex problems and achieve remarkable results in various industries. The DDPG algorithm’s unique approach to continuous action spaces and its ability to learn optimal policies through experience have set it apart from other reinforcement learning methods.
DDPG algorithms have demonstrated their potential in a wide range of applications, from robotics and autonomous driving to resource management and beyond. By enabling AI systems to learn from experience and adapt to changing environments, DDPG algorithms have opened up new possibilities for innovation and progress in various fields. Moreover, the ongoing research in DDPG algorithms, including multi-agent DDPG, hierarchical DDPG, and continuous control with DDPG, has the potential to address some of the challenges of scalability, generalization, and complexity in various applications.
In conclusion, DDPG algorithms have played a crucial role in advancing AI and reinforcement learning, providing a valuable tool for solving complex problems and driving innovation in various industries. As research in this field continues to evolve, we can expect to see even more innovative and creative concepts that provide value and usefulness to the reader. The future of DDPG algorithms is bright, and their impact on AI and reinforcement learning will continue to grow in the years to come.

