Covariance of a Matrix Python

Understanding Covariance: A Foundation for Data Analysis

Covariance measures how much two variables change together. A positive covariance suggests that when one variable increases, the other tends to increase as well. Conversely, a negative covariance indicates that as one variable rises, the other tends to fall. A covariance of zero implies little to no linear relationship between the variables. Understanding the covariance of a matrix is crucial because it reveals the relationships between multiple variables simultaneously, providing insights that individual analyses might miss. For example, analyzing the covariance of a matrix containing stock prices can help investors understand how different stocks move in relation to each other, informing diversification strategies. Similarly, examining the covariance of a matrix of temperature and ice cream sales data reveals how these variables are related; in warmer months, ice cream sales are likely to be higher. This understanding is vital for forecasting and decision-making across diverse fields.

The concept of covariance extends beyond simple pairs of variables. When dealing with datasets containing numerous variables, calculating the covariance of a matrix provides a comprehensive view of the interrelationships within the data. This is particularly useful in portfolio management, where understanding the covariance between different assets is vital for risk assessment and optimization. In climate science, for instance, analyzing the covariance of a matrix of weather patterns helps researchers understand how various weather events are connected and predict future climate changes. Furthermore, the covariance of a matrix serves as a foundation for many advanced statistical techniques, including principal component analysis (PCA) and linear regression models, which are used extensively in machine learning and data analysis. Calculating and interpreting the covariance of a matrix in Python is therefore a key skill for anyone working with multivariate data.

Mastering the calculation and interpretation of the covariance of a matrix in Python opens doors to sophisticated data analysis. Python’s NumPy library offers powerful tools to compute covariance efficiently, enabling researchers and analysts to uncover hidden relationships in complex datasets. This understanding informs decisions in various applications, from financial modeling and risk assessment to scientific discovery and predictive analytics. The ability to perform this analysis effectively is essential for data-driven decision-making in a wide range of fields. The covariance of a matrix python implementation provides the tools necessary for this level of analysis. Its applications are vast, spanning diverse domains and providing crucial insights for informed decision-making.

Visualizing Covariance: Unveiling Relationships in Data

Understanding the covariance of a matrix is significantly easier with visual aids. Scatter plots effectively illustrate the relationship between two variables. A positive covariance shows points clustered along a line with a positive slope. As one variable increases, the other tends to increase. For example, a positive covariance might exist between hours studied and exam scores. A negative covariance, conversely, displays points along a line with a negative slope. Here, as one variable increases, the other tends to decrease. Ice cream sales and the number of winter coats sold could exhibit a negative covariance. Zero covariance indicates no linear relationship; the points on the scatter plot show no clear pattern. The calculation of the covariance of a matrix python reflects these visual patterns. A high positive or negative value corresponds to a strong linear relationship, while a value near zero suggests a weak or nonexistent relationship. Examining these visual representations alongside the numerical covariance strengthens understanding.

Consider three datasets. The first shows a strong positive correlation between variables X and Y, resulting in a high positive covariance. The scatter plot clearly displays points clustered closely around a line with a positive slope. The second dataset presents a negative relationship, with points concentrated around a line of negative slope, yielding a significantly negative covariance. The third dataset exhibits a weak or no relationship between X and Y, creating a near-zero covariance. The scatter plot for this dataset shows a random dispersion of points with no discernible pattern. These examples highlight the powerful connection between visual representation and numerical calculation for the covariance of a matrix in Python. Mastering this connection is key to interpreting results accurately.

Different covariance values directly translate to different visual patterns in scatter plots. Understanding this visual representation is crucial for interpreting the covariance of a matrix calculated using Python. For instance, a large positive covariance indicates a strong positive linear relationship easily visualized as points tightly clustered around a line with a positive slope. In contrast, a small negative covariance would indicate a weak negative linear relationship shown by a more dispersed scatter of points around a line with a negative slope. A covariance close to zero would reflect a weak or no linear relationship, visualized as a random distribution of points on the scatter plot. This visual approach provides a clear intuitive understanding of covariance, crucial for effective data analysis and accurate interpretation of the covariance of a matrix python. The ability to connect numerical results with visual representations enhances one’s ability to extract meaningful insights from data.

Calculating Covariance Manually: A Step-by-Step Guide

Calculating the covariance of a matrix manually provides a foundational understanding of this crucial statistical concept. This process illuminates the underlying calculations before leveraging the efficiency of NumPy. Consider a simple 2×2 matrix as an example. To compute the covariance of a matrix Python offers a step-by-step approach. First, calculate the mean of each column. Then, for each data point, subtract its column’s mean. Next, multiply these differences for each corresponding data point across columns. Sum these products. Finally, divide by (n-1), where n is the number of data points, to obtain the covariance. This manual calculation emphasizes the core principles involved in determining the covariance of a matrix in Python.

Let’s illustrate with a concrete example. Suppose we have a matrix representing the daily returns of two stocks: [[0.02, 0.01], [0.03, 0.02], [0.01, 0.00]]. The mean of the first column (stock A) is 0.02, and the mean of the second column (stock B) is 0.01. Subtracting the means from each data point, we get: [[-0.00, 0.00], [0.01, 0.01], [-0.01, -0.01]]. Next, multiply corresponding elements and sum the products: (-0.00 * 0.00) + (0.01 * 0.01) + (-0.01 * -0.01) = 0.0002. Finally, divide by (3-1) = 2, resulting in a covariance of 0.0001. This positive covariance suggests a tendency for the two stock returns to move together. Understanding this manual process strengthens one’s grasp of the covariance of a matrix Python computation provides. This method allows a deeper understanding of the covariance of a matrix Python libraries then automate.

The formula for calculating the covariance between two variables X and Y is: Cov(X,Y) = Σ[(xi – μx)(yi – μy)] / (n-1), where xi and yi are individual data points, μx and μy are the means of X and Y, and n is the number of data points. Extending this to a matrix involves calculating the covariance between all pairs of columns. The diagonal elements of the resulting covariance matrix represent the variances of the individual variables, while the off-diagonal elements represent the covariances between pairs of variables. Mastering this manual calculation is essential for truly understanding the covariance of a matrix Python-based solutions build upon. Efficient Python code utilizing NumPy significantly streamlines this process for larger datasets, but a manual calculation using a small matrix serves as a valuable educational tool for grasping the core concept of the covariance of a matrix.

How to Compute Matrix Covariance Efficiently with NumPy

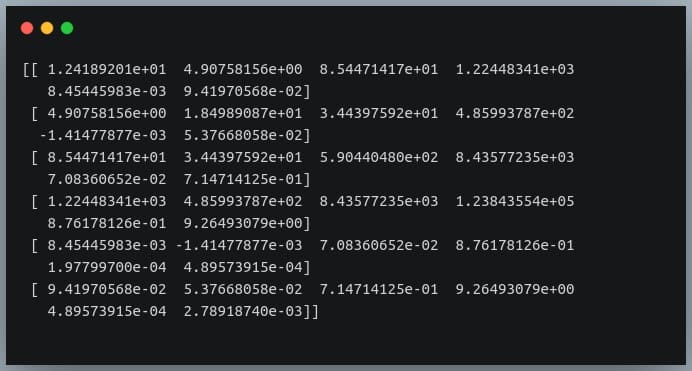
NumPy provides the function numpy.cov() for efficient covariance of a matrix python calculations. This function takes a data array as input and returns the covariance matrix. The input can be a 2D array where each row represents a variable and each column represents an observation, or it can be a Pandas DataFrame. For example, a 2D array representing three variables (x, y, z) with five observations would be a 3×5 array. The function calculates the sample covariance by default; to obtain the population covariance, set the bias parameter to True. Understanding how to correctly format your data is crucial for accurate results in the calculation of the covariance of a matrix python.

Let’s illustrate with examples. First, consider a simple 2D NumPy array: data = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]]). The covariance matrix is computed using: covariance_matrix = np.cov(data). The output will be a 3×3 matrix, where the diagonal elements represent the variances of each variable (x, y, z), and the off-diagonal elements represent the covariances between pairs of variables. Similarly, if you have data in a Pandas DataFrame, you can pass the DataFrame directly to np.cov() after selecting the relevant numerical columns. Remember that np.cov() assumes that variables are represented as rows. Incorrect data arrangement is a frequent cause of error. Always verify your data’s orientation before calculating the covariance of a matrix python using NumPy. NumPy handles missing values (NaNs) by ignoring them in the calculation, but it is generally good practice to handle missing values appropriately beforehand.

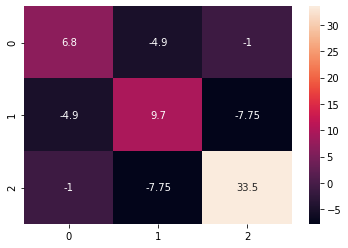
Interpreting the output is straightforward. The diagonal elements show the variance of each variable. Large variances indicate high variability. The off-diagonal elements represent the covariances between variables. A positive covariance suggests a positive relationship (when one variable increases, the other tends to increase). A negative covariance indicates a negative relationship (one increases, the other tends to decrease). Values close to zero suggest a weak or no linear relationship. For instance, a high positive covariance between stock prices of two companies might suggest that they are correlated. Conversely, a negative covariance between temperature and ice cream sales could indicate an inverse relationship, where high temperatures result in decreased ice cream sales. This accurate interpretation of covariance of a matrix python is crucial for data-driven decisions. Understanding and effectively using the numpy.cov() function is key to performing efficient covariance calculations in Python, providing valuable insights into the relationships within your data.

Interpreting the Covariance Matrix: Understanding the Results

The covariance matrix, a key output of calculating the covariance of a matrix in Python using NumPy, provides a comprehensive view of the relationships between variables within a dataset. Each element in this matrix holds significant meaning. The diagonal elements represent the variances of individual variables. Variance quantifies how spread out the data points are for each variable. A higher variance indicates greater dispersion. For example, a high variance in stock prices suggests significant price fluctuations. Understanding these variances is crucial for assessing the volatility of individual variables. The covariance of a matrix python calculation allows for this comprehensive understanding.

More insightful are the off-diagonal elements. These elements represent the covariances between pairs of variables. A positive covariance signifies that the variables tend to move together. When one variable increases, the other also tends to increase. For instance, a positive covariance between ice cream sales and temperature reflects the common-sense relationship: higher temperatures lead to increased ice cream sales. A negative covariance suggests an inverse relationship; when one variable increases, the other tends to decrease. Consider the covariance of a matrix python example involving stock prices of two competing companies. A negative covariance could indicate that when one stock performs well, the other tends to underperform. The magnitude of the covariance indicates the strength of the relationship; a larger absolute value suggests a stronger association, while a covariance near zero indicates a weak or no relationship.

Interpreting the covariance matrix involves careful consideration of both the magnitude and sign of each element. This allows for a detailed understanding of variable interdependencies. The covariance of a matrix Python calculation provides more than just numbers; it reveals the underlying structure and relationships within your data. This information is invaluable for various applications, from financial modeling and risk assessment to machine learning algorithm development. By accurately calculating and interpreting the covariance of a matrix using Python, one gains valuable insights into complex datasets and relationships between variables. The ability to interpret the covariance matrix is paramount for leveraging the power of the covariance of a matrix Python computations in practical applications.

Dealing with Different Data Types and Handling Missing Values in Covariance of a Matrix Python

Calculating the covariance of a matrix in Python often involves dealing with real-world datasets. These datasets may contain missing values or variables of different types. Missing data points can significantly skew covariance calculations, leading to inaccurate results. Simple techniques like listwise deletion (removing rows with any missing values) can lead to a substantial loss of data and biased estimates, especially with larger datasets. A more robust approach involves imputation, where missing values are replaced with estimated values. Common imputation methods include mean imputation (replacing missing values with the mean of the column), median imputation, or more sophisticated techniques like k-Nearest Neighbors imputation. The choice of imputation method depends on the nature of the data and the extent of missingness. Remember, the goal is to minimize bias while preserving as much information as possible when computing the covariance of a matrix python.

When working with different data types, the covariance calculation requires careful consideration. The covariance of a matrix python is primarily defined for numerical data. Categorical variables, often represented as strings or integers, cannot be directly used in standard covariance computations. To include categorical data in the analysis, one must convert them into a numerical representation. Techniques like one-hot encoding can transform categorical variables into multiple binary variables, representing each unique category. Other methods, such as label encoding or target encoding, assign numerical values to categories based on specific criteria. However, this preprocessing needs to be considered carefully, as the choice of encoding method can affect the interpretation of the covariance. The covariance of a matrix python calculation will now reflect relationships involving these newly encoded numerical features.

Data transformation is another crucial aspect of preprocessing. If the data exhibits significant skewness or outliers, these characteristics can disproportionately influence the covariance calculation. Transformations like logarithmic transformations or Box-Cox transformations can help stabilize variance and improve the reliability of the covariance of a matrix python estimate. Standardization or normalization techniques, which center and scale the data, are particularly useful when comparing variables with different units or scales. These preprocessing steps ensure that the covariance calculation is accurate, reliable, and meaningful, improving the overall quality of the analysis and enhancing the validity of any conclusions derived from the covariance of a matrix python.

Advanced Applications of Covariance: Beyond the Basics

Covariance analysis extends far beyond basic calculations. Understanding the covariance of a matrix in Python unlocks powerful techniques in multivariate data analysis. One key application is the creation of correlation matrices. A correlation matrix normalizes the covariance matrix, revealing the strength and direction of linear relationships between variables, regardless of their scales. This provides a clearer picture than the raw covariance values. The covariance of a matrix is fundamental to this process.

Principal Component Analysis (PCA) heavily relies on the covariance of a matrix. PCA is a dimensionality reduction technique. It transforms a dataset with many correlated variables into a smaller set of uncorrelated variables, called principal components. These components capture the most significant variance in the data. The covariance matrix serves as the foundation for identifying the principal components and their corresponding directions. Effectively utilizing the covariance of a matrix in Python simplifies PCA implementation and interpretation.

Furthermore, the covariance of a matrix plays a vital role in numerous machine learning algorithms. Many algorithms, such as linear discriminant analysis (LDA) and support vector machines (SVMs), directly use or implicitly rely on covariance information for feature selection, classification, and regression tasks. Understanding how covariance affects these models helps in model optimization and interpretation. For instance, the covariance of a matrix informs decisions regarding feature scaling and regularization. Mastering the covariance of a matrix in Python enhances your capabilities in building and improving machine learning models.

Troubleshooting Common Errors and Pitfalls When Calculating the Covariance of a Matrix in Python

Calculating the covariance of a matrix in Python, using NumPy’s numpy.cov() function, is generally straightforward. However, several common pitfalls can lead to incorrect results or errors. One frequent mistake involves incorrect data input. The function expects a 2D array or a Pandas DataFrame where each column represents a variable. Inputting data in the wrong format, such as a 1D array or a list of lists with inconsistent lengths, will result in errors. Always double-check your data’s structure before using numpy.cov(). Remember, understanding the covariance of a matrix is crucial for accurate analysis.

Another common issue arises from misinterpreting the output covariance matrix. The diagonal elements represent the variances of individual variables. Off-diagonal elements show the covariances between pairs of variables. A positive covariance indicates a tendency for variables to move together, while a negative covariance suggests an inverse relationship. However, the magnitude of the covariance alone doesn’t directly indicate the strength of the relationship. To assess the strength, one should calculate the correlation coefficient. Failing to differentiate between covariance and correlation is a frequent source of misinterpretations when working with the covariance of a matrix in Python. Always carefully examine the covariance matrix and consider further analysis, like correlation, for a complete understanding.

Finally, misapplying the numpy.cov() function itself can lead to problems. For instance, forgetting to specify the rowvar parameter correctly (defaulting to rowvar=True, where each row represents a variable) can produce incorrect results if your data is organized with variables as columns. Similarly, not handling missing values appropriately before computation will introduce biases in the covariance calculation. NumPy’s numpy.nancov() provides a solution for handling missing data (represented as NaN). Understanding the implications of missing data and applying appropriate pre-processing steps, like imputation, is essential for accurate covariance analysis. Correctly handling these aspects of covariance of a matrix python calculations ensures reliable and meaningful results.