Unlocking the Power of Diversification
Portfolio risk management is a crucial aspect of investment strategy, as it enables investors to minimize potential losses while maximizing returns. One of the most effective ways to manage risk is through diversification, which involves spreading investments across different asset classes to reduce exposure to any one particular market or sector. By diversifying a portfolio, investors can reduce their overall risk profile and increase the potential for long-term growth. However, diversification is not just about randomly selecting a mix of assets; it requires a deep understanding of how these assets interact with each other. This is where covariance analysis comes into play, providing a powerful tool for identifying the optimal mix of assets that will provide the highest returns for a given level of risk. By applying the covariance formula in portfolio management, investors can unlock the full potential of diversification and achieve their investment goals.
Understanding Covariance: A Key to Portfolio Optimization
Covariance is a statistical measure that plays a vital role in portfolio management, enabling investors to understand the relationship between different assets in a portfolio. In essence, covariance measures the extent to which two assets move in tandem with each other, providing valuable insights into the potential risks and returns of a portfolio. By analyzing the covariance between different assets, investors can identify opportunities to diversify their portfolio, reduce risk, and increase potential returns. The covariance formula in portfolio management is a powerful tool for achieving this goal, allowing investors to quantify the relationship between assets and make informed investment decisions. In this context, understanding covariance is essential for unlocking the full potential of portfolio optimization.
How to Calculate Covariance for Portfolio Optimization
Calculating covariance is a crucial step in portfolio optimization, as it enables investors to quantify the relationship between different assets in a portfolio. The covariance formula in portfolio management is a powerful tool for achieving this goal. To calculate covariance, follow these steps: First, gather historical data on the returns of the assets in your portfolio. Next, calculate the mean returns of each asset over the specified time period. Then, subtract the mean returns from each asset’s returns to obtain the deviations from the mean. Finally, multiply the deviations of each asset together and sum them up to obtain the covariance. The covariance formula can be expressed mathematically as Cov(X, Y) = Σ[(Xi – X̄)(Yi – Ȳ)] / (n – 1), where Cov(X, Y) is the covariance between assets X and Y, Xi and Yi are the individual returns, X̄ and Ȳ are the mean returns, and n is the number of observations. By applying this formula, investors can calculate the covariance between different assets and make informed decisions about their portfolio composition.
The Covariance Formula: A Mathematical Approach
The covariance formula in portfolio management is a mathematical expression that quantifies the linear relationship between two assets in a portfolio. Mathematically, the covariance formula is represented as Cov(X, Y) = Σ[(Xi – X̄)(Yi – Ȳ)] / (n – 1), where Cov(X, Y) is the covariance between assets X and Y, Xi and Yi are the individual returns, X̄ and Ȳ are the mean returns, and n is the number of observations. This formula is based on the concept of deviations from
Interpreting Covariance Results for Informed Investment Decisions
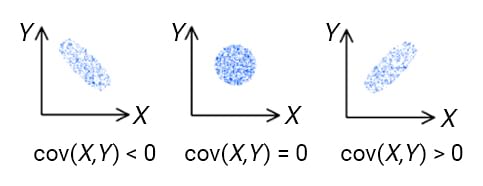
Once the covariance formula in portfolio management has been applied to calculate the covariance between different assets, the next step is to interpret the results. This involves understanding the implications of positive, negative, and zero covariance on investment decisions. A positive covariance indicates that the assets tend to move in the same direction, while a negative covariance suggests that they move in opposite directions. A zero covariance implies that the assets are unrelated. By analyzing the covariance results, investors can identify opportunities to diversify their portfolios and reduce risk. For instance, if two assets have a negative covariance, including both in a portfolio can help reduce overall risk. On the other hand, if two assets have a high positive covariance, it may be wise to limit exposure to one or both of them to avoid amplifying risk. By leveraging covariance analysis, investors can make informed decisions about their portfolio composition and optimize their investment strategies.
Real-World Applications of Covariance in Portfolio Management
Covariance analysis has numerous real-world applications in portfolio management, and its significance is evident in the success stories of various investment firms and financial institutions. One notable example is the use of covariance in constructing diversified portfolios. By analyzing the covariance between different assets, investors can identify opportunities to reduce risk and increase returns. For instance, a study by Vanguard found that a diversified portfolio with a mix of stocks and bonds can reduce risk by up to 30% compared to a portfolio invested solely in stocks. This is because the covariance between stocks and bonds is typically negative, meaning that when stock prices fall, bond prices tend to rise.
Another example is the use of covariance in risk parity strategies. This approach involves allocating portfolio weights based on the covariance of different assets, rather than their volatility. By doing so, investors can create a more balanced portfolio that is less susceptible to market fluctuations. A study by the Journal of Portfolio Management found that risk parity strategies outperformed traditional portfolio optimization methods in terms of risk-adjusted returns.
In addition, covariance analysis is used in asset allocation decisions, where investors need to determine the optimal mix of assets to achieve their investment objectives. By analyzing the covariance between different asset classes, investors can identify the most efficient allocation and minimize risk. For instance, a study by BlackRock found that a portfolio with a mix of equities, fixed income, and alternative assets can provide a more stable return profile compared to a portfolio invested solely in equities.
These examples demonstrate the practical applications of covariance analysis in portfolio management. By leveraging the covariance formula in portfolio management, investors can make more informed decisions, reduce risk, and increase returns. As the investment landscape continues to evolve, the importance of covariance analysis in portfolio management is likely to grow.
Common Pitfalls to Avoid in Covariance Analysis
While covariance analysis is a powerful tool for portfolio optimization, it is not immune to errors and pitfalls. Investors and portfolio managers must be aware of these common mistakes to avoid them and ensure accurate results. One common pitfall is data quality issues, where incorrect or incomplete data can lead to inaccurate covariance calculations. This can occur when using historical data that is not representative of current market conditions or when failing to account for data outliers.
Another pitfall is sampling errors, where the sample size is too small or not representative of the population. This can lead to biased covariance estimates and incorrect investment decisions. For instance, if a portfolio manager uses a sample of only 10 stocks to estimate covariance, the results may not be representative of the entire market.
Incorrect assumptions are also a common pitfall in covariance analysis. For example, assuming that asset returns are normally distributed when they are not can lead to inaccurate covariance estimates. Additionally, failing to account for non-linear relationships between assets can also lead to incorrect results.
Furthermore, investors must be aware of the limitations of the covariance formula in portfolio management. The formula assumes that the relationship between assets is linear, which may not always be the case. Additionally, the formula does not account for extreme events or tail risks, which can have a significant impact on portfolio performance.
To avoid these pitfalls, investors and portfolio managers must ensure that they use high-quality data, account for sampling errors, and make accurate assumptions about asset returns. By doing so, they can ensure that their covariance analysis is accurate and reliable, and that their investment decisions are informed and effective.
Best Practices for Implementing Covariance in Your Portfolio Strategy
Implementing covariance analysis into a portfolio management strategy requires a thoughtful and structured approach. To get the most out of covariance analysis, investors and portfolio managers should follow best practices that ensure accurate and reliable results. One key best practice is to integrate covariance analysis with other risk management tools, such as value-at-risk (VaR) and expected shortfall (ES). This allows for a comprehensive understanding of portfolio risk and enables more informed investment decisions.
Another best practice is to regularly update and refine covariance estimates to reflect changing market conditions. This can be achieved by using rolling windows of historical data or by incorporating real-time market data into the analysis. By doing so, investors can ensure that their covariance estimates remain accurate and relevant.
In addition, investors should consider using alternative covariance estimation methods, such as shrinkage estimators or Bayesian approaches, to improve the accuracy and robustness of their results. These methods can help to reduce estimation errors and provide more reliable covariance estimates.
When implementing covariance analysis, it is also essential to consider the covariance formula in portfolio management and its limitations. For example, investors should be aware of the assumptions underlying the covariance formula and take steps to address any potential biases or inaccuracies. By doing so, they can ensure that their covariance analysis is accurate and reliable.
Finally, investors should consider using covariance analysis in conjunction with other portfolio optimization techniques, such as mean-variance optimization or Black-Litterman models. This can help to create a more comprehensive and effective portfolio management strategy that takes into account multiple sources of risk and return.
By following these best practices, investors and portfolio managers can effectively incorporate covariance analysis into their portfolio management strategy and make more informed investment decisions. By leveraging the power of covariance analysis, investors can create more diversified and resilient portfolios that are better equipped to navigate complex and volatile markets.