What is Variance and Why Does it Matter?
In statistics, variance is a measure of the spread or dispersion of a dataset, providing valuable insights into the distribution of values. It’s a crucial concept in understanding and analyzing data, as it helps identify patterns, trends, and correlations within a dataset. Variance is essential in making informed decisions and predictions, as it enables data analysts and scientists to quantify the uncertainty associated with a dataset. In essence, variance answers the question of how much individual data points deviate from the mean value. This fundamental concept has far-reaching implications in various fields, including finance, engineering, and social sciences, where it’s used to make accurate forecasts and recommendations. As we delve into the world of variance, a common question arises: can variance be a negative number? While we’ll address this question later, it’s essential to first understand the importance of variance in data analysis and decision-making.
Can Variance Ever be a Negative Number?
In traditional statistics, the answer to this question is a resounding no. Variance, by definition, is a measure of the spread or dispersion of a dataset, and it cannot be a negative number. This is because variance is calculated as the average of the squared differences between each data point and the mean value. As a result, the variance is always a non-negative value, as the squared differences can never be negative. This fundamental property of variance is rooted in the mathematical concept of squared deviations, which ensures that variance is always a positive or zero value. So, can variance be a negative number? The short answer is no, and this limitation is a direct consequence of the mathematical definition of variance.
How to Calculate Variance: A Step-by-Step Guide
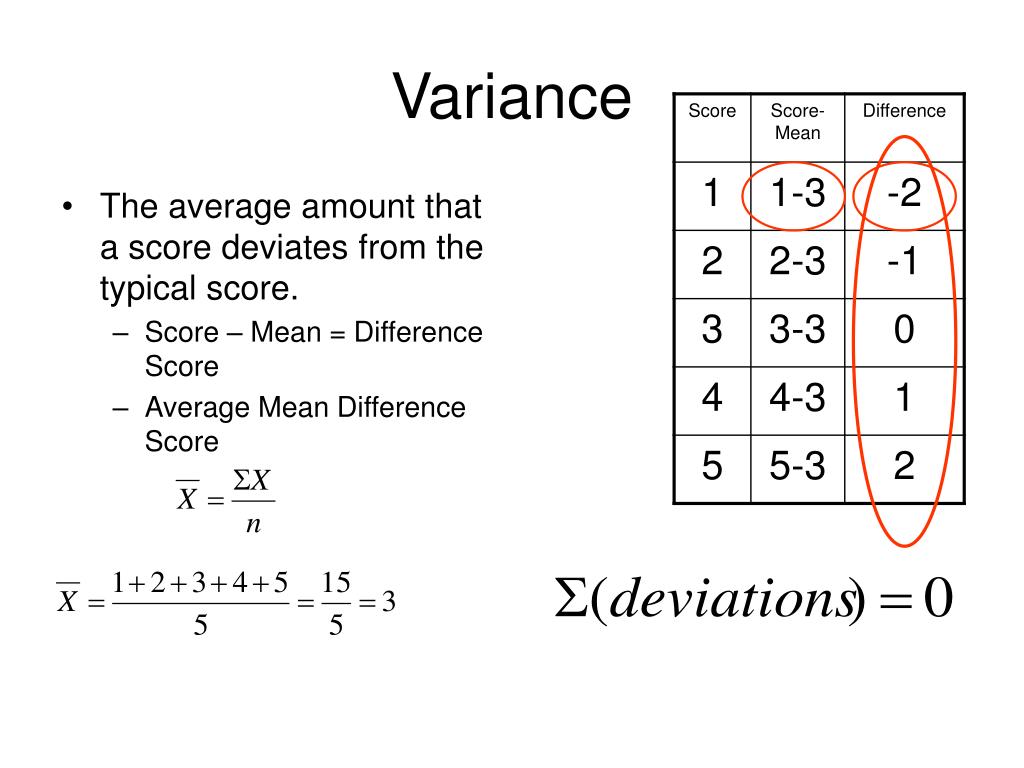
Calculating variance is a straightforward process that involves a few simple steps. The formula for calculating variance is: σ² = Σ(xi – μ)² / (n – 1), where σ² is the variance, xi is each data point, μ is the mean, and n is the number of data points. To break it down further, follow these steps:
Step 1: Calculate the mean (μ) of the dataset by summing up all the data points and dividing by the number of data points (n).
Step 2: Subtract the mean (μ) from each data point (xi) to find the deviations from the mean.
Step 3: Square each deviation (xi – μ)² to ensure all values are positive.
Step 4: Sum up the squared deviations Σ(xi – μ)².
Step 5: Divide the sum of the squared deviations by the number of data points minus one (n – 1) to find the variance (σ²).
For example, let’s say we have a dataset of exam scores: 80, 70, 90, 85, and 75. To calculate the variance, we would first calculate the mean, which is 80. Then, we would subtract the mean from each data point to find the deviations: -10, -10, 10, 5, and -5. Next, we would square each deviation: 100, 100, 100, 25, and 25. The sum of the squared deviations is 350, and dividing by the number of data points minus one (5 – 1 = 4) gives us a variance of 87.5.
By following these steps, you can calculate the variance of any dataset, which is essential for understanding the spread of data and making informed decisions in various fields, including finance, engineering, and social sciences. Remember, can variance be a negative number? No, it cannot, as it’s a measure of the spread of data, and the squared deviations ensure a non-negative value.
The Difference Between Variance and Standard Deviation
Variance and standard deviation are two closely related statistical concepts that are often confused with one another. While they are both measures of the spread of data, they serve distinct purposes and are used in different contexts.
Variance, as we’ve discussed, is a measure of the spread of data, calculated as the average of the squared differences between each data point and the mean. It’s a measure of how spread out the data is from the mean value.
Standard deviation, on the other hand, is the square root of the variance. It’s a measure of the amount of variation or dispersion of a set of values. Standard deviation is often used to understand the volatility of a dataset, and it’s a more intuitive measure than variance.
The key difference between variance and standard deviation lies in their units. Variance is measured in the units squared, while standard deviation is measured in the same units as the data. For example, if we’re measuring the heights of individuals in inches, the variance would be in inches squared, while the standard deviation would be in inches.
In practice, variance is often used in statistical modeling and hypothesis testing, while standard deviation is used to understand the spread of data and make predictions. For instance, in finance, standard deviation is used to calculate the risk of an investment, while variance is used to model the behavior of stock prices.
It’s essential to understand the distinction between variance and standard deviation to avoid misinterpreting results and making incorrect conclusions. Remember, can variance be a negative number? No, it cannot, as it’s a measure of the spread of data, and the squared deviations ensure a non-negative value. By grasping the differences between variance and standard deviation, you’ll be better equipped to tackle complex data analysis challenges and make informed decisions.
Real-World Applications of Variance in Data Analysis
Variance plays a crucial role in various fields, including finance, engineering, and social sciences, where data analysis is essential for making informed decisions and predictions. In finance, variance is used to calculate the risk of an investment, helping investors to make informed decisions about their portfolios. For instance, a stock with high variance is considered riskier than one with low variance, as its price can fluctuate more dramatically.
In engineering, variance is used to optimize system performance and reliability. By analyzing the variance of a system’s output, engineers can identify areas for improvement and make adjustments to reduce variability and increase efficiency. In quality control, variance is used to monitor and improve the consistency of manufacturing processes.
In social sciences, variance is used to understand the spread of social and economic phenomena, such as income inequality and crime rates. By analyzing the variance of these metrics, researchers can identify patterns and trends that inform policy decisions and social programs.
In healthcare, variance is used to analyze the effectiveness of treatments and identify areas for improvement. By calculating the variance of patient outcomes, healthcare professionals can identify the most effective treatments and make data-driven decisions about patient care.
These examples illustrate the importance of variance in real-world data analysis. By understanding variance, professionals in various fields can make informed decisions, optimize systems, and improve outcomes. Remember, can variance be a negative number? No, it cannot, as it’s a measure of the spread of data, and the squared deviations ensure a non-negative value. By applying variance analysis to real-world problems, professionals can unlock the power of data and drive meaningful change.
Common Misconceptions About Variance and How to Avoid Them
Despite its importance in statistics, variance is often misunderstood, leading to common misconceptions that can have significant consequences in data analysis. One of the most prevalent misconceptions is that variance can be a negative number. However, as we’ve discussed earlier, variance cannot be negative in traditional statistics due to the mathematical properties of squared deviations.
Another common misconception is that variance is the same as standard deviation. While they are related, variance and standard deviation are distinct statistical concepts with different applications. Understanding the differences between these two concepts is crucial to avoid misinterpreting results and making incorrect conclusions.
To avoid these mistakes, it’s essential to have a solid understanding of the mathematical foundations of variance and its applications in data analysis. Here are some tips to keep in mind:
- Always check the units of variance, as it’s measured in squared units, whereas standard deviation is measured in the same units as the data.
- Be cautious when interpreting variance values, as high variance doesn’t necessarily imply high risk or uncertainty.
- Avoid using variance as a measure of central tendency, as it’s a measure of spread, not location.
By being aware of these common misconceptions and taking steps to avoid them, data analysts can ensure that their results are accurate and reliable. Remember, can variance be a negative number? No, it cannot, and understanding this fundamental property is crucial for making informed decisions in data analysis.
Variance in Modern Statistics: New Developments and Trends
In recent years, variance calculation has undergone significant advancements, expanding the possibilities of variance analysis in various fields. One of the notable developments is robust variance estimation, which provides a more accurate and reliable measure of variance in the presence of outliers or non-normal data. This approach has been particularly useful in finance, where robust variance estimation helps to better capture the risk of investment portfolios.
Another trend in modern statistics is the increasing use of Bayesian approaches to variance analysis. Bayesian methods offer a more flexible and adaptive framework for modeling variance, allowing for the incorporation of prior knowledge and uncertainty. This has led to the development of more sophisticated variance models, capable of handling complex data structures and relationships.
Additionally, the rise of machine learning and artificial intelligence has opened up new avenues for variance analysis. Techniques such as variance-based feature selection and variance regularization have been developed to improve the performance of machine learning models. These advancements have far-reaching implications for fields such as engineering, social sciences, and healthcare, where variance analysis plays a critical role in decision-making.
While traditional statistics has established that variance cannot be a negative number, modern developments have pushed the boundaries of variance analysis, enabling researchers and practitioners to tackle complex problems with greater precision and accuracy. As data analysis continues to evolve, it’s essential to stay informed about the latest trends and advancements in variance calculation, ensuring that we can unlock the full potential of variance in driving informed decisions and predictions.
Conclusion: Unlocking the Power of Variance in Data Analysis
In conclusion, understanding variance is crucial in statistics, as it provides valuable insights into the spread of data. By grasping the concept of variance, data analysts can make informed decisions and predictions in various fields, from finance to social sciences. Remember, can variance be a negative number? No, it cannot, and recognizing this fundamental property is essential for accurate data analysis.
This article has provided a comprehensive overview of variance, covering its definition, calculation, and real-world applications. We’ve also explored common misconceptions about variance and discussed recent advancements in variance calculation. By applying the knowledge gained from this article, readers can unlock the power of variance in their own data analysis challenges.
As data analysis continues to evolve, it’s essential to stay informed about the latest developments and trends in variance calculation. By doing so, we can harness the full potential of variance to drive informed decisions, improve predictions, and unlock new insights in various fields. With a solid understanding of variance, the possibilities for data analysis are endless.