What Does it Mean to be Differentiable?
In the realm of calculus, differentiability is a fundamental concept that plays a crucial role in understanding the behavior of functions. A function is said to be differentiable at a point if its limit exists at that point, and the function can be expressed as a linear approximation near that point. This concept is essential in calculus, as it enables the calculation of rates of change and slopes of tangents, which are used to model real-world phenomena, such as motion, growth, and optimization.
The concept of differentiability is closely tied to the concept of limits. A limit represents the value that a function approaches as the input (or x-value) gets arbitrarily close to a specific point. When a function is differentiable at a point, it means that the limit exists, and the function can be expressed as a linear approximation near that point. This property is vital in calculus, as it enables the calculation of derivatives, which are used to model real-world phenomena.
Differentiability is a local property, meaning it only depends on the behavior of the function near a point, rather than its global behavior. This means that a function can be differentiable at a single point, but not necessarily differentiable at every point in its domain. Understanding this local property is vital in applying calculus to real-world problems, as it enables us to analyze and model complex phenomena with precision. Moreover, it raises an important question: can something be differentiable but not continuous? This question highlights the nuances of differentiability and continuity, and it’s essential to understand these concepts to apply calculus effectively.
In essence, differentiability is a powerful tool that allows us to study the behavior of functions in detail. By understanding the concept of differentiability, we can gain insights into the nature of functions and their applications in various fields. Whether it’s modeling population growth, optimizing functions, or understanding physical systems, differentiability plays a crucial role in helping us make sense of the world around us. As we delve deeper into the world of calculus, it becomes increasingly important to understand the intricacies of differentiability and its relationship with continuity.
The Role of Continuity in Differentiability
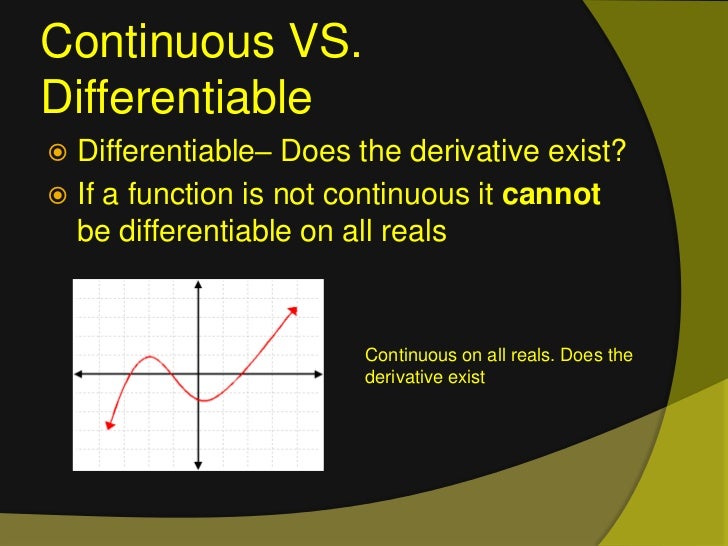
In calculus, differentiability and continuity are two fundamental concepts that are closely related, yet distinct. While differentiability implies continuity, the converse is not always true. In other words, a function can be continuous at a point, but not necessarily differentiable at that point. This subtle distinction is crucial in understanding the behavior of functions and their applications in various fields.
To illustrate this relationship, consider a function that is continuous at a point, but has a sharp corner or a cusp at that point. Such a function is not differentiable at that point, as the limit of the function does not exist or is infinite. On the other hand, a function that is differentiable at a point is necessarily continuous at that point, as the limit of the function exists and is finite.
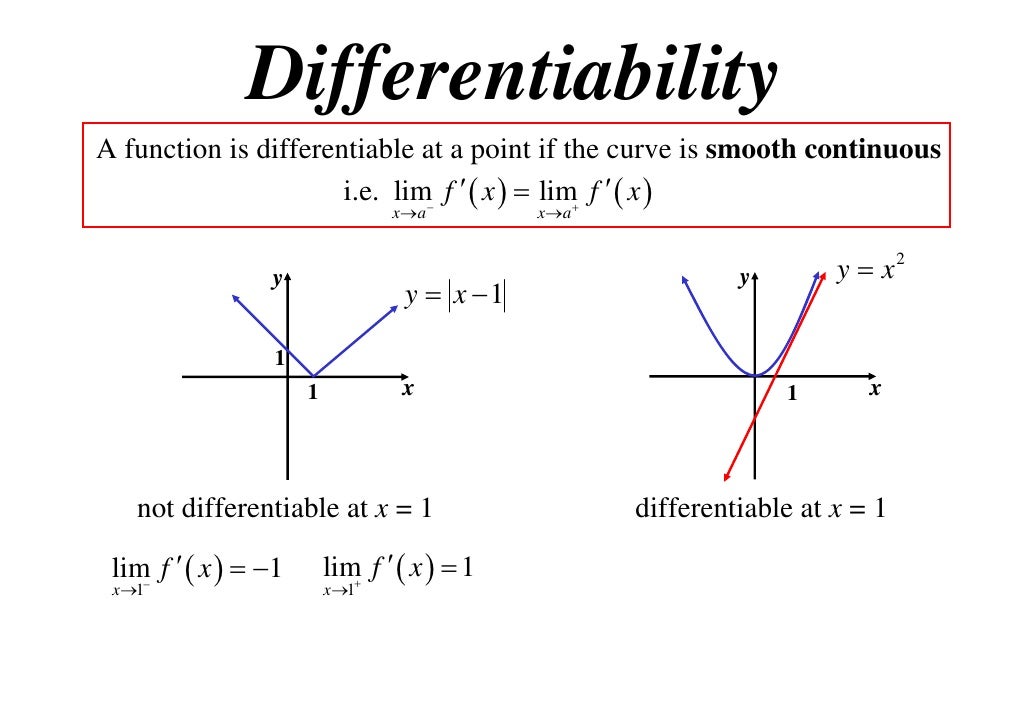
Examples of functions that are continuous but not differentiable abound. For instance, the absolute value function, |x|, is continuous at x = 0, but not differentiable at that point, as the limit of the function does not exist. Similarly, the function f(x) = x^2 sin(1/x) is continuous at x = 0, but not differentiable at that point, as the limit of the function oscillates wildly.
The importance of understanding the relationship between differentiability and continuity cannot be overstated. In many real-world applications, such as physics, engineering, and economics, functions that are continuous but not differentiable can lead to unexpected behavior or singularities. By recognizing the distinction between these two concepts, we can better model and analyze complex phenomena, and avoid potential pitfalls.
In the next section, we will explore how to identify functions that are differentiable but not continuous, and examine some concrete examples of such functions. The question remains: can something be differentiable but not continuous? The answer lies in the nuances of differentiability and continuity, and understanding these concepts is essential to unlocking the secrets of calculus.
How to Identify Functions that are Differentiable but not Continuous
Identifying functions that are differentiable but not continuous requires a combination of mathematical techniques and graphical analysis. One approach is to examine the limit of the function as the input approaches a specific point. If the limit exists, but is not finite, then the function is not continuous at that point. However, if the limit exists and is finite, then the function may be differentiable at that point, but not necessarily continuous.
Another technique is to analyze the derivative of the function. If the derivative exists at a point, but is not continuous at that point, then the function is differentiable but not continuous. This can be done using various differentiation rules, such as the power rule, product rule, and quotient rule.
Graphical analysis is also a powerful tool for identifying functions that are differentiable but not continuous. By examining the graph of the function, we can identify points where the function is not continuous, such as corners, cusps, or vertical tangents. These points may indicate that the function is differentiable but not continuous.
For example, consider the function f(x) = |x|. This function is differentiable at x = 0, but not continuous at that point, as the limit of the function does not exist. Similarly, the function f(x) = x^2 sin(1/x) is differentiable at x = 0, but not continuous at that point, as the limit of the function oscillates wildly.
In summary, identifying functions that are differentiable but not continuous requires a combination of mathematical techniques, graphical analysis, and a deep understanding of the nuances of differentiability and continuity. By mastering these techniques, we can better understand the behavior of functions and their applications in various fields. The question remains: can something be differentiable but not continuous? The answer lies in the careful analysis of functions and their properties.
Examples of Functions that Defy Intuition
In the realm of calculus, there exist functions that defy intuition and challenge our understanding of differentiability and continuity. Two such examples are the Dirichlet function and the Weierstrass function.
The Dirichlet function, also known as the Dirichlet’s function, is defined as f(x) = 1 if x is rational and f(x) = 0 if x is irrational. This function is differentiable at every point, but not continuous at any point. This may seem counterintuitive, as we often associate differentiability with continuity. However, the Dirichlet function demonstrates that this is not always the case.
The Weierstrass function, on the other hand, is a continuous function that is not differentiable at any point. This function is defined as f(x) = ∑[n=0 to ∞] (b^n \* cos(a^n \* π \* x)), where a and b are constants. The Weierstrass function is a classic example of a function that is continuous but not differentiable, and it has played a significant role in the development of calculus.
These functions are important in calculus because they highlight the nuances of differentiability and continuity. They demonstrate
The Importance of Understanding Differentiability and Continuity
In real-world applications, understanding the difference between differentiability and continuity is crucial for making accurate predictions and modeling complex phenomena. In physics, for instance, differentiability is essential for describing the motion of objects, while continuity is vital for understanding the behavior of physical systems. Similarly, in engineering, differentiability is used to optimize system performance, while continuity is necessary for ensuring the stability of structures.
In economics, differentiability is used to model the behavior of economic systems, while continuity is essential for understanding the impact of policy changes. Moreover, in computer science, differentiability is used in machine learning algorithms, while continuity is necessary for ensuring the smooth operation of computer systems.
Despite its importance, the distinction between differentiability and continuity is often overlooked, leading to incorrect assumptions and flawed models. For example, assuming that a function is continuous simply because it is differentiable can lead to errors in optimization problems. Similarly, failing to recognize that a function is not continuous can result in incorrect predictions in physical systems.
Therefore, it is essential to understand the nuances of differentiability and continuity, and to recognize that can something be differentiable but not continuous. By doing so, we can develop more accurate models, make better predictions, and create more efficient systems. In the end, a deep understanding of differentiability and continuity is crucial for advancing our knowledge in various fields and for solving complex problems.
Common Misconceptions and Pitfalls
When working with differentiable and continuous functions, it’s essential to avoid common misconceptions and pitfalls that can lead to incorrect assumptions and flawed models. One of the most common mistakes is assuming that differentiability implies continuity, which is not always the case. In fact, can something be differentiable but not continuous? The answer is yes, and understanding this nuance is crucial for making accurate predictions and modeling complex phenomena.
Another common pitfall is assuming that a function is continuous simply because it is defined at a point. This is not necessarily true, as a function can be defined at a point but still be discontinuous. For example, the function f(x) = 1/x is defined at x = 0, but it is not continuous at that point.
Students and professionals may also encounter difficulties when dealing with functions that have multiple discontinuities or singularities. In such cases, it’s essential to carefully analyze the function’s behavior near each discontinuity or singularity to determine its differentiability and continuity.
Additionally, graphical analysis can sometimes be misleading, as a function may appear to be continuous or differentiable when it is not. Therefore, it’s essential to use a combination of analytical and graphical techniques to verify the properties of a function.
By being aware of these common misconceptions and pitfalls, individuals can avoid making incorrect assumptions and develop a deeper understanding of differentiability and continuity. This, in turn, can lead to more accurate models, better predictions, and more efficient solutions in various fields.
Visualizing Differentiability and Continuity
Visual aids, such as graphs and charts, can be powerful tools for illustrating the concepts of differentiability and continuity. By visualizing the behavior of a function, individuals can gain a deeper understanding of its properties and develop a more intuitive sense of how it behaves. For example, a graph can help identify points of discontinuity or non-differentiability, allowing individuals to better understand the function’s behavior near those points.
In addition, visualization can help to clarify the relationship between differentiability and continuity. By comparing the graphs of functions that are differentiable but not continuous, such as the Dirichlet function, with those that are continuous but not differentiable, such as the absolute value function, individuals can gain a better understanding of the nuances of these concepts.
Furthermore, visualization can also help to illustrate the importance of understanding the difference between differentiability and continuity in real-world applications. For instance, in physics, the graph of a function representing the motion of an object can help to identify points of non-differentiability, which can correspond to sudden changes in velocity or acceleration.
Moreover, visualization can also facilitate the identification of functions that can something be differentiable but not continuous. By analyzing the graph of a function, individuals can identify points where the function is not continuous, but still differentiable, such as the function f(x) = x^2 sin(1/x) at x = 0.
In conclusion, visualization is a powerful tool for understanding the concepts of differentiability and continuity. By using graphs and charts to illustrate these concepts, individuals can gain a deeper understanding of the properties of functions and develop a more intuitive sense of how they behave.
Conclusion: Unraveling the Complexity of Differentiability and Continuity
In conclusion, the concepts of differentiability and continuity are fundamental to calculus and its applications. Understanding the nuances of these concepts is crucial for making accurate predictions and modeling complex phenomena. As we have seen, differentiability implies continuity, but not the other way around, and can something be differentiable but not continuous? The answer is yes, and understanding this distinction is vital for avoiding common misconceptions and pitfalls.
By recognizing the importance of differentiability and continuity in real-world applications, such as physics, engineering, and economics, individuals can develop a deeper appreciation for the power of calculus in modeling and analyzing complex systems. Furthermore, by employing visual aids, such as graphs and charts, individuals can gain a more intuitive understanding of these concepts and develop a deeper understanding of the behavior of functions.
In summary, the key takeaways from this article are: differentiability is a local property that depends on the behavior of a function near a point; differentiability implies continuity, but not the other way around; and understanding the distinction between differentiability and continuity is crucial for avoiding common misconceptions and pitfalls. By grasping these concepts, individuals can unlock the full potential of calculus and develop a deeper understanding of the world around them.