Why Understanding Portfolio Variance Matters
Portfolio variance is a crucial metric in investment decision-making, as it measures the dispersion of returns around the mean. Accurately calculating the variance of a portfolio is essential for investors and portfolio managers to understand the potential risks and rewards associated with their investments. By grasping the concept of portfolio variance, investors can make informed decisions about asset allocation, risk management, and performance evaluation. In essence, portfolio variance serves as a key indicator of a portfolio’s overall risk profile, enabling investors to adjust their strategies accordingly. In this article, we will explore the significance of portfolio variance, its calculation, and its applications in investment decision-making, highlighting the importance of mastering this critical aspect of portfolio risk management.
How to Calculate Portfolio Variance: A Comprehensive Approach
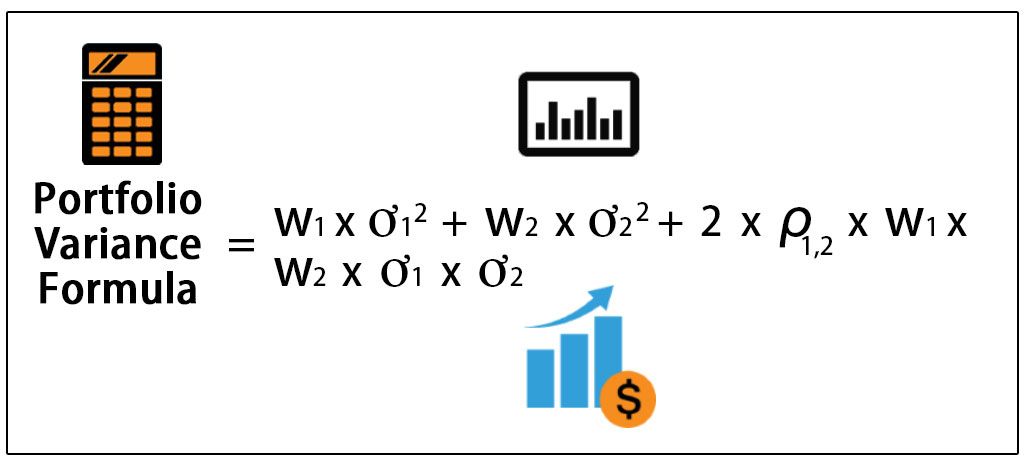
Calculating the variance of a portfolio is a crucial step in understanding its risk profile. The formula to calculate portfolio variance involves the weights of individual assets, their returns, and the covariance between them. The formula can be represented as: σp² = Σ wi² * σi² + Σ Σ wij * σi * σj, where σp² is the portfolio variance, wi is the weight of asset i, σi² is the variance of asset i, and wij is the covariance between assets i and j. To calculate the variance of a portfolio, investors must first determine the weights of each asset, then calculate the returns and covariance of each asset. Finally, the formula can be applied to calculate the portfolio variance. It is essential to accurately calculate the variance of a portfolio to make informed investment decisions and manage risk effectively.
The Role of Diversification in Reducing Portfolio Variance
Diversification is a crucial strategy in portfolio management, as it helps to reduce portfolio variance and overall risk. By spreading investments across different asset classes, industries, and geographic regions, investors can minimize their exposure to any one particular market or sector. This, in turn, reduces the portfolio’s sensitivity to market fluctuations, leading to a more stable return profile. Diversification can be achieved through various means, including investing in a mix of stocks, bonds, and alternative assets, as well as allocating assets across different regions and sectors. By doing so, investors can reduce their portfolio’s reliance on any one asset, thereby decreasing the overall variance of the portfolio. Effective diversification can help investors to calculate the variance of a portfolio more accurately, leading to better-informed investment decisions and improved risk management.
Common Pitfalls to Avoid When Calculating Portfolio Variance
When calculating the variance of a portfolio, investors must be aware of common pitfalls that can lead to inaccurate results. One of the most common mistakes is ignoring correlations between assets, which can significantly impact the overall portfolio variance. Failing to account for correlations can result in an underestimation of portfolio risk, leading to poor investment decisions. Another common error is using incorrect or outdated data, which can lead to inaccurate calculations of returns and covariance. Additionally, investors may incorrectly assume that historical data is representative of future market conditions, leading to an inaccurate estimation of portfolio variance. To avoid these errors, investors should ensure that they use accurate and up-to-date data, account for correlations between assets, and consider multiple scenarios when calculating the variance of a portfolio. By doing so, investors can ensure that their calculations are accurate and reliable, enabling them to make informed investment decisions and effectively manage risk.
Using Historical Data to Estimate Portfolio Variance
Historical data plays a crucial role in estimating portfolio variance, as it provides a basis for understanding the behavior of different assets and their interactions. When using historical data to calculate the variance of a portfolio, it is essential to select an appropriate time period and data frequency. A longer time period can provide a more comprehensive understanding of the portfolio’s behavior, but it may also be influenced by outdated market conditions. Conversely, a shorter time period may be more relevant to current market conditions, but it may not capture the full range of potential outcomes. The data frequency, whether daily, weekly, or monthly, also impacts the accuracy of the estimation. A higher frequency can provide a more detailed understanding of the portfolio’s behavior, but it may also be more susceptible to noise and volatility. By carefully selecting the time period and data frequency, investors can use historical data to estimate portfolio variance and make more informed investment decisions. This, in turn, enables them to calculate the variance of a portfolio more accurately and effectively manage risk.
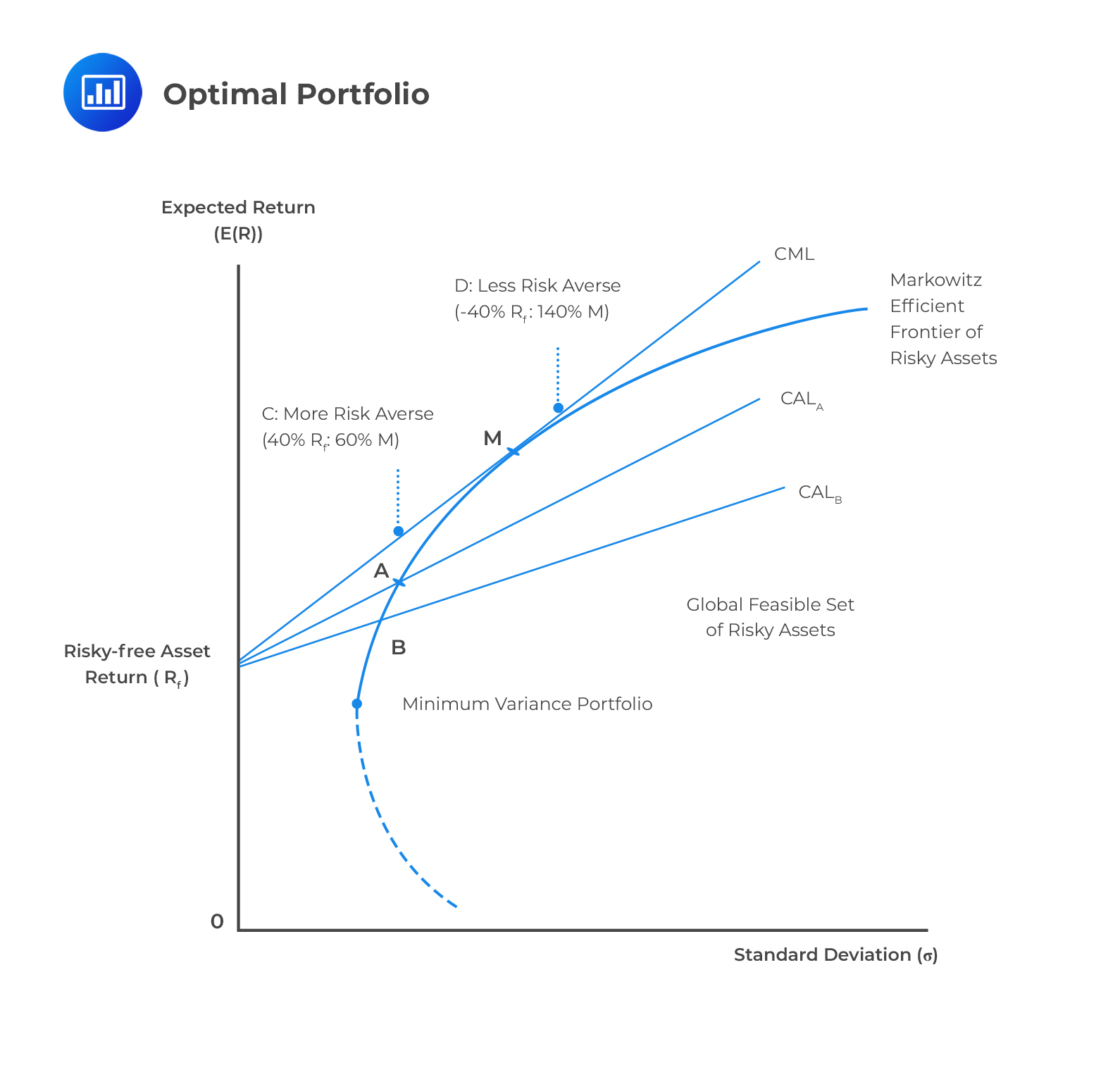
The Relationship Between Portfolio Variance and Expected Returns
The relationship between portfolio variance and expected returns is a fundamental concept in investment decision-making. In general, investors expect higher returns for taking on greater risk, as measured by portfolio variance. This trade-off between risk and potential returns is a critical consideration when constructing a portfolio. A portfolio with high variance may offer higher potential returns, but it also increases the likelihood of significant losses. Conversely, a portfolio with low variance may provide more stable returns, but it may also limit potential gains. To calculate the variance of a portfolio effectively, investors must understand this relationship and strike a balance between risk and potential returns. By doing so, they can create a portfolio that aligns with their investment objectives and risk tolerance. This, in turn, enables them to make informed investment decisions and achieve their long-term financial goals.
Portfolio Variance in Practice: Real-World Examples and Case Studies
A thorough understanding of portfolio variance is crucial in investment decision-making, and its application can be seen in various real-world examples. For instance, a pension fund may use portfolio variance to determine the optimal asset allocation, balancing risk and potential returns to ensure a stable income stream for retirees. Similarly, a hedge fund may employ portfolio variance to identify and manage risk, maximizing returns while minimizing potential losses. In another example, an individual investor may calculate the variance of a portfolio to determine the optimal mix of stocks and bonds, aligning their investment strategy with their risk tolerance and financial goals. By examining these real-world examples and case studies, investors can gain a deeper understanding of how portfolio variance is used in practice, and how it can be applied to achieve successful investment outcomes. This, in turn, enables them to calculate the variance of a portfolio effectively and make informed investment decisions.
Conclusion: Effective Portfolio Variance Calculation for Informed Investment Decisions
In conclusion, accurately calculating the variance of a portfolio is a crucial step in investment decision-making. By understanding the concept of portfolio variance, investors can effectively measure and manage risk, making informed decisions that align with their investment objectives and risk tolerance. Throughout this guide, we have covered the importance of portfolio variance, the steps involved in calculating it, and its application in real-world scenarios. By avoiding common pitfalls, using historical data, and understanding the relationship between portfolio variance and expected returns, investors can create a portfolio that balances risk and potential returns. Effective portfolio variance calculation is essential for achieving long-term financial goals, and by following the steps outlined in this guide, investors can make informed investment decisions and navigate the complexities of portfolio risk management.