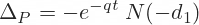Black Scholes Formula With Dividends

Decoding Option Valuation with Future Income Streams

In the realm of financial derivatives, options pricing stands as a critical element for investors and traders alike. The standard Black-Scholes model, a cornerstone of option valuation, provides a framework for estimating the theoretical price of European-style options. However, its original formulation assumes that the underlying asset, typically a stock, does not pay dividends during the option’s lifetime. This assumption is often unrealistic, as many companies distribute dividends to their shareholders.

When the underlying asset pays dividends, the standard Black-Scholes model requires modification to accurately reflect the impact of these payouts on the option’s price. Dividends represent a cash flow received by the shareholder, which effectively reduces the stock’s price on the ex-dividend date. This reduction, in turn, affects the potential payoff of the option, necessitating an adjustment to the valuation model. Therefore, the dividend payments influence the option prices and must be accounted for when using the black scholes formula with dividends.

The presence of dividends generally has a negative impact on call option prices and a positive impact on put option prices. This is because dividends reduce the stock price, making it less likely that a call option will be in the money at expiration and more likely that a put option will be. Several approaches exist to incorporate dividends into the Black-Scholes model, ranging from discrete dividend adjustments to continuous dividend yield models. Understanding these adjustments is crucial for accurately pricing options on dividend-paying stocks, using a sound black scholes formula with dividends, and making informed trading decisions. Ignoring dividends can lead to significant mispricing and potential losses, underlining the importance of the black scholes formula with dividends.

How to Calculate Option Prices Considering Dividends

Calculating option prices on dividend-paying stocks requires adjusting the standard Black-Scholes model. The core principle involves accounting for the present value of expected dividends, as these payouts reduce the stock’s price appreciation potential. Therefore, the standard Black-Scholes formula must be modified to reflect this reduction. This adjustment ensures a more accurate option price, incorporating the impact of future dividend payments. The adjusted model is still referred to as the black scholes formula with dividends. This adjustment is crucial for precise option valuation.

The key adjustment involves subtracting the present value of expected dividends from the current stock price. This modified stock price is then used in the Black-Scholes formula. The formula considers factors like the strike price, time to expiration, risk-free interest rate, and volatility. To calculate the present value of expected dividends, each dividend payment must be discounted back to the present using the risk-free interest rate. Summing the present values of all expected dividends provides the total dividend impact on the stock price. Using the black scholes formula with dividends provides a more accurate option valuation. It’s essential to accurately forecast dividend amounts and payment dates to ensure the present value calculation’s precision.

For example, consider a stock trading at $100, with an expected dividend of $2 to be paid in three months. Assuming a risk-free interest rate of 5% per year, the present value of the dividend is $2 / (1 + (0.05/4)) = $1.975. The adjusted stock price, reflecting the dividend impact, is $100 – $1.975 = $98.025. This adjusted stock price of $98.025, rather than the original $100, is then inputted into the Black-Scholes formula to calculate the call and put option prices. By following these steps, one can accurately apply the black scholes formula with dividends. In summary, the modified black scholes formula with dividends provides a more realistic option price. This meticulous approach allows for a more reliable valuation of options on dividend-paying stocks.

Understanding the Dividend Yield’s Influence on Option Values

The dividend yield plays a crucial role in the adjusted Black-Scholes formula, impacting option values significantly. The dividend yield is calculated by dividing the annual dividends per share by the stock’s price. It represents the return on investment an investor receives through dividends alone, without considering capital appreciation. When pricing options on dividend-paying stocks using the black scholes formula with dividends, this yield needs careful consideration.

The black scholes formula with dividends incorporates the dividend yield to adjust the stock price. A higher dividend yield reduces the call option price and increases the put option price. This is because a higher dividend payout reduces the stock’s future price appreciation potential. Consequently, call options, which benefit from price increases, become less valuable. Conversely, put options, which benefit from price decreases, become more valuable as the stock price is expected to grow less. Scenarios with varying dividend yields illustrate this impact effectively.

Consider these scenarios to see how the black scholes formula with dividends is impacted:

• High Dividend Yield: A stock with a high dividend yield will have relatively lower call option prices and higher put option prices compared to a similar stock with a lower yield. This is because the market anticipates less capital appreciation due to the large dividend payouts.
• Low Dividend Yield: A stock with a low dividend yield exhibits the opposite effect. Call option prices will be higher, and put option prices will be lower, reflecting the greater potential for price appreciation.
• No Dividend: When a stock pays no dividends, the standard Black-Scholes model can be applied directly without any dividend adjustments. The dividend yield is essentially zero, removing its impact on option pricing.

A table or graph can visually represent this relationship, illustrating how option prices change with varying dividend yields. For example, plotting call and put option prices against different dividend yield values would clearly show the inverse relationship between call prices and dividend yields, and the direct relationship between put prices and dividend yields when applying the black scholes formula with dividends.

Comparing Approaches: Discrete Dividends vs. Continuous Dividend Yield

When adapting the Black Scholes formula with dividends, two primary methods exist for incorporating the impact of dividend payments: the discrete dividend approach and the continuous dividend yield approach. Each method offers distinct advantages and disadvantages, making one more suitable than the other depending on the specific characteristics of the underlying asset and the desired level of precision.

The discrete dividend approach involves subtracting the present value of each expected future dividend from the current stock price before applying the standard Black Scholes formula with dividends. This method is particularly useful when dealing with a small number of well-defined dividend payments, such as those associated with companies that declare dividends on a quarterly basis. The advantage of the discrete dividend approach lies in its accuracy when the timing and amount of dividends are known with reasonable certainty. However, it becomes more complex and less practical when dealing with a large number of dividend payments or when the dividend amounts are uncertain. Furthermore, accurately predicting the exact payment dates and amounts can be challenging, introducing potential errors into the option pricing calculation. This adjustment to the stock price is critical in using the black scholes formula with dividends.

Conversely, the continuous dividend yield approach assumes that dividends are paid out continuously over time at a constant rate. This rate, known as the dividend yield, is typically expressed as a percentage of the stock price per year. In this approach, the Black Scholes formula with dividends is modified by reducing the stock’s growth rate by the dividend yield. This method is simpler to implement than the discrete dividend approach, especially when dealing with assets that pay dividends frequently or when a precise forecast of individual dividend payments is unavailable. The continuous dividend yield approach is often preferred for modeling options on stock indices or exchange-traded funds (ETFs) that hold a basket of dividend-paying stocks. However, its simplicity comes at the cost of accuracy, as it assumes a constant dividend payout, which may not always be the case in reality. The choice between these approaches depends on the trade-off between simplicity and accuracy, considering the nature of the underlying asset and the specific requirements of the option pricing model. Therefore, understanding the nuances of each approach is crucial for effectively applying the Black Scholes formula with dividends.

Analyzing the Limitations of the Dividend-Adjusted Black-Scholes Model

The dividend-adjusted Black-Scholes model offers a valuable framework for option pricing when dividends are involved. However, it is important to acknowledge its limitations. These limitations stem from the underlying assumptions of the original Black-Scholes model and the added complexities of dividend forecasting. Several factors can affect the accuracy of the model when calculating option prices, especially when considering dividends. These should be considered before implementing the black scholes formula with dividends.

One major limitation is the assumption of constant volatility. The Black-Scholes model assumes that the volatility of the underlying asset remains constant over the option’s life. In reality, volatility fluctuates, particularly around dividend announcement and payment dates. These fluctuations can significantly impact option prices, rendering the model less accurate. Another critical assumption is the accuracy of dividend forecasts. The dividend-adjusted Black-Scholes model requires accurate estimates of future dividend payments. However, dividends are not guaranteed and can be reduced, increased, or even suspended by the company’s board of directors. Inaccurate dividend forecasts will lead to inaccurate option price calculations using the black scholes formula with dividends. Furthermore, the model typically assumes that dividends are paid out at discrete intervals or as a continuous yield. This may not always reflect the actual dividend payment schedule of a company, introducing further inaccuracies.

Moreover, the black scholes formula with dividends does not account for all real-world complexities. Factors such as transaction costs, taxes, and early exercise possibilities (for American-style options) are not incorporated. These factors can influence the actual trading price of options. The model also struggles to accurately price options on stocks with highly volatile dividend policies or those undergoing significant corporate actions. While the dividend-adjusted Black-Scholes model provides a useful starting point, more sophisticated models exist. These advanced models address some of the limitations mentioned above. For example, some models incorporate stochastic volatility, which allows volatility to change randomly over time. Other models use more complex dividend forecasting techniques or consider the possibility of early exercise. Traders should be aware of these limitations and consider using more advanced models when appropriate to refine option pricing strategies using the black scholes formula with dividends.

Practical Examples: Applying the Formula to Real-World Stocks

To illustrate the application of the dividend-adjusted Black-Scholes formula, consider several real-world examples. These examples will demonstrate how to calculate call and put option prices for stocks that pay dividends, utilizing estimated or announced dividend information. Using the black scholes formula with dividends involves adjusting the stock price to reflect the present value of future dividend payments.

Example 1: Apple Inc. (AAPL). Assume Apple stock is trading at $170. The strike price for a call option is $175, expiring in 3 months (0.25 years). The risk-free interest rate is 5%. Apple is expected to pay a dividend of $0.23 per share in one month. The volatility is estimated at 25%. First, calculate the present value of the dividend: $0.23 * e^(-0.05 * (1/12)) ≈ $0.229. The dividend-adjusted stock price is $170 – $0.229 = $169.771. Now, input these values into the black scholes formula with dividends to find the call option price. Similarly, a put option with the same parameters can be calculated.

Example 2: Verizon Communications Inc. (VZ). Verizon stock trades at $50. A put option has a strike price of $48, expiring in 6 months (0.5 years). The risk-free rate is 5%. Verizon is expected to pay two dividends of $0.65 each, one in 2 months and another in 5 months. Calculate the present value of each dividend: $0.65 * e^(-0.05 * (2/12)) ≈ $0.645 and $0.65 * e^(-0.05 * (5/12)) ≈ $0.637. The total present value of dividends is $0.645 + $0.637 = $1.282. The adjusted stock price is $50 – $1.282 = $48.718. Utilizing the dividend-adjusted stock price in the black scholes formula with dividends will provide the theoretical put option price. It’s crucial to accurately estimate dividends for the black scholes formula with dividends to be effective. By using different company stocks, a better picture of this model and black scholes formula with dividends can be visualized.

Strategies for Trading Options on Dividend-Paying Stocks

Trading options on dividend-paying stocks requires a nuanced understanding of how dividends affect option prices. The dividend-adjusted black scholes formula with dividends becomes an essential tool for developing effective trading strategies. One such strategy involves capitalizing on anticipated dividend payouts. Before a dividend’s ex-date, call option prices may increase, while put option prices may decrease, reflecting the expected reduction in the stock price after the dividend is paid. Traders can strategically buy calls or sell puts before the ex-date, aiming to profit from these price movements. However, it’s crucial to consider transaction costs and the risk of unexpected changes in the stock price.

Hedging dividend risk is another important aspect of trading options on dividend-paying stocks. Investors holding a long stock position can use put options to protect against potential price declines following a dividend payout. By purchasing put options, investors create a price floor for their stock holdings, limiting their downside risk. The cost of the put option is offset by the dividend income received. The dividend-adjusted black scholes formula with dividends aids in determining the appropriate strike price and expiration date for the put options, considering the expected dividend amount and the investor’s risk tolerance.

Furthermore, understanding the “Greeks” – delta, gamma, theta, vega, and rho – is crucial for managing option positions on dividend-paying stocks. Delta measures the sensitivity of an option’s price to changes in the underlying stock price. Gamma measures the rate of change of delta. Theta measures the time decay of an option. Vega measures the sensitivity of an option’s price to changes in volatility. Rho measures the sensitivity of an option’s price to changes in interest rates. In the context of dividend-paying stocks, it is useful to consider dividend adjustments to the Greeks. Specifically, dividend payments can affect the stock price, which in turn impacts the option’s delta. Before the ex-dividend date, the delta of a call option may be higher because the option holder is entitled to the future stock price, which includes the dividend value. After the ex-dividend date, the delta typically decreases. Traders use the black scholes formula with dividends to adjust the Greeks. By carefully analyzing the Greeks and their sensitivities to dividend payouts, option traders can make more informed decisions and manage their risk effectively when employing the black scholes formula with dividends.

Impact of Dividend Changes on Option Pricing: A Scenario Analysis

Changes in dividend payouts can significantly influence the prices of call and put options, creating potential trading opportunities. An unexpected dividend increase typically leads to a decrease in the call option price and an increase in the put option price. Conversely, a dividend cut generally results in an increase in the call option price and a decrease in the put option price. These price movements stem from the fact that higher dividends reduce the attractiveness of holding the underlying stock, as a portion of the expected return is received as dividends rather than potential capital appreciation. The adjusted black scholes formula with dividends reflects these changes, as the present value of future dividends directly impacts the calculated option price.

Consider a stock currently trading at $100, with a call option expiring in three months and a strike price of $100. Initially, the company is expected to pay a $1 dividend one month from now. Using the black scholes formula with dividends, we can calculate the call option price. Now, suppose the company announces an unexpected increase in the dividend to $2. This higher dividend will reduce the stock’s price appreciation potential, leading to a decrease in the call option price. The magnitude of the change will depend on factors such as the time to expiration, the strike price, and the volatility of the underlying stock. Conversely, if the company announces it will suspend its dividend payment altogether, the call option price will likely increase. Analyzing these scenarios through the lens of the black scholes formula with dividends highlights the sensitivity of option prices to dividend changes.

Visual representations, such as graphs depicting call and put option prices under different dividend scenarios, can provide valuable insights. For example, a graph could illustrate how the call option price decreases linearly with increasing dividend amounts, while the put option price increases. Traders can use this information to develop strategies that capitalize on anticipated dividend announcements. One strategy involves buying put options on stocks before an expected dividend increase or buying call options before an expected dividend decrease. These strategies aim to profit from the anticipated price movements of the options following the dividend announcement, using the black scholes formula with dividends to estimate the potential price change. It’s crucial to remember that the black scholes formula with dividends is a model and may not perfectly predict actual market prices, so risk management is essential.