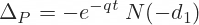Pricing Options with Dividends: A Practical Guide
This article provides a practical guide on pricing options when the underlying asset pays dividends. Dividends are distributions of a company’s earnings to its shareholders, typically in the form of cash or stock. These payments impact option prices because they reduce the potential appreciation of the underlying asset. Consequently, the standard Black-Scholes model, a widely used option pricing tool, requires adjustments to accurately reflect the influence of dividends. Understanding how to incorporate dividends into option pricing models is crucial for investors and traders seeking to manage risk and make informed decisions in the options market. The accurate calculation of option prices for dividend-paying assets relies on understanding the nuances of the
The payment of dividends affects the price of call and put options. Dividends essentially lower the future expected price of the stock. This is because when a company pays a dividend, its stock price typically decreases by the amount of the dividend. The adjusted
The
How to Calculate Fair Option Value Considering Dividends
This section introduces the fundamental concept that dividend yield reduces the underlying asset’s price, directly influencing option valuation. Dividends effectively lower the expected future price of the stock because a portion of the company’s value is distributed to shareholders. Consequently, this anticipated price reduction impacts both call and put option values. The payout of dividends gives investors an expectation for diminished stock appreciation over time, as the company’s retained earnings are lower than they would be without the dividend distribution. Understanding this adjustment is crucial for accurately pricing options, especially when employing models like the black scholes formula with dividends.
The intuition behind this adjustment is straightforward. Call options derive their value from the potential for the underlying asset’s price to increase. If a stock pays dividends, its price is likely to be lower on the ex-dividend date than it would have been otherwise. This reduces the potential upside for call option holders, decreasing the call option’s value. Conversely, put options gain value when the underlying asset’s price decreases. The expected price decline due to dividends increases the likelihood that the put option will be in the money at expiration, boosting the put option’s value. Therefore, the black scholes formula with dividends needs to accurately reflect this inverse relation.
To calculate the fair option value, one must account for the present value of expected dividends over the option’s life. This is typically done by subtracting the present value of these dividends from the current stock price before applying the standard Black-Scholes model, or by incorporating a continuous dividend yield, ‘q,’ directly into the formula. The continuous dividend yield represents the annualized dividend payment as a percentage of the stock price, assuming dividends are constantly being paid. By understanding the impact dividends have on stock price appreciation, investors can better utilize the black scholes formula with dividends to inform their investment and trading decisions. This dividend-adjusted approach provides a more accurate and reliable option pricing assessment.
Exploring the Dividend-Adjusted Black-Scholes Formula
The standard Black-Scholes model requires adjustment when pricing options on dividend-paying assets. The dividend-adjusted Black-Scholes formula incorporates the impact of dividends on the underlying asset‘s price. This adjustment is crucial for a more accurate option valuation. Here’s the formula:
C = S * e-qT * N(d1) – K * e-rT * N(d2)
Where:
- C = Call option price
- S = Current stock price
- K = Strike price
- r = Risk-free interest rate
- T = Time to expiration (in years)
- σ = Volatility of the stock price
- q = Continuous dividend yield
- N(x) = Cumulative standard normal distribution function
d1 and d2 are calculated as follows:
d1 = [ln(S/K) + (r – q + (σ2/2)) * T] / (σ * sqrt(T))
d2 = d1 – σ * sqrt(T)
The key addition to the original Black-Scholes formula is the ‘q’ term, representing the continuous dividend yield. This ‘q’ value discounts the current stock price (S) by a factor of e-qT. This adjustment accounts for the expected decrease in the stock price due to dividend payouts over the option’s lifetime. By continuously paying out dividends, this effectively reduces the potential appreciation of the underlying asset, thus influencing the option’s value. Utilizing the black scholes formula with dividends helps to make the right decision on buying call or put options.
The black scholes formula with dividends enables traders to more effectively assess potential gains in their stock, and can improve investing strategies overall. It’s important to be aware of all factors when buying and selling options, and the black scholes formula with dividends gives traders insight in how to most effectively adjust their strategies.
Ultimately, accurately determining the variable ‘q’ is a crucial element in getting an accurate result from the black scholes formula with dividends. Making the right decision involves getting precise values for all inputs to the formula, and making sure that the continuous dividend yield is as accurate as possible. Investors need to remember that this is just a model, but it gives an outline of how to make smart decisions.
A Step-by-Step Example: Applying the Modified Formula
Context_4: This section demonstrates the practical application of the dividend-adjusted Black-Scholes formula with dividends. It offers a clear, step-by-step calculation. Consider a hypothetical stock trading at $50 (S = 50). An investor wants to price a call option on this stock. The option has a strike price of $55 (K = 55). It expires in 6 months (T = 0.5 years). The risk-free interest rate is 5% (r = 0.05). The stock pays a continuous dividend yield of 2% (q = 0.02). The stock’s volatility is 30% (σ = 0.30).
First, adjust the stock price for the dividend yield: S’ = S * exp(-qT) = 50 * exp(-0.02 * 0.5) = 50 * exp(-0.01) ≈ 50 * 0.99005 ≈ $49.50. Now, use this adjusted stock price (S’) in the Black-Scholes formula with dividends to calculate d1 and d2. d1 = [ln(S’/K) + (r + σ^2/2)T] / (σ√T) = [ln(49.50/55) + (0.05 + 0.30^2/2) * 0.5] / (0.30 * √0.5) = [ln(0.9) + (0.05 + 0.045) * 0.5] / (0.30 * 0.707) = [-0.105 + 0.0475] / 0.2121 ≈ -0.0575 / 0.2121 ≈ -0.271. Next, d2 = d1 – σ√T = -0.271 – 0.30 * √0.5 = -0.271 – 0.2121 ≈ -0.483. Find the cumulative standard normal distribution values for d1 and d2. N(d1) = N(-0.271) ≈ 0.3936. N(d2) = N(-0.483) ≈ 0.3145. Finally, calculate the call option price using the formula: C = S’ * N(d1) – K * exp(-rT) * N(d2) = 49.50 * 0.3936 – 55 * exp(-0.05 * 0.5) * 0.3145 = 49.50 * 0.3936 – 55 * exp(-0.025) * 0.3145 = 19.483 – 55 * 0.9753 * 0.3145 = 19.483 – 16.855 ≈ $2.63. Therefore, the estimated fair value of the call option, considering the dividend yield, is approximately $2.63.
This example illustrates how the dividend-adjusted Black-Scholes formula with dividends modifies the standard calculation. The dividend yield reduces the present value of the stock. This, in turn, lowers the call option price. The black scholes formula with dividends provides a more precise valuation. The adjustment is crucial when pricing options on dividend-paying stocks. Ignoring dividends can lead to significant pricing errors. Especially for options with longer times to expiration or higher dividend yields. The black scholes formula with dividends and the dividend yield ‘q’, represent the continuous payout from the asset.
The Impact of Dividend Yield on Call and Put Options
Dividend yield significantly influences call and put option prices. The black scholes formula with dividends demonstrates this relationship clearly. Higher dividend yields generally lead to lower call option prices. This is because a larger dividend payment reduces the expected future stock price appreciation. Investors anticipate less capital gain when a stock pays substantial dividends.
Conversely, higher dividend yields typically increase put option prices. The expectation of a lower future stock price, due to the dividend payout, makes put options more valuable. Investors are more likely to profit from a put option if the stock price declines. This dynamic is a crucial aspect of understanding the black scholes formula with dividends. To illustrate, consider two identical stocks, Stock A and Stock B. Stock A pays a high dividend yield, while Stock B pays a negligible dividend. A call option on Stock A will likely be priced lower than a call option on Stock B, all other factors being equal. Similarly, a put option on Stock A will likely be priced higher than a put option on Stock B.
The black scholes formula with dividends allows for a more accurate assessment of option values in dividend-paying stocks. For example, imagine a stock with a current price of $100. A call option with a strike price of $105 and a time to expiration of one year might be priced at $8 using the standard Black-Scholes model. However, if the stock pays a dividend yield of 5%, the dividend-adjusted Black-Scholes model would likely result in a lower call option price, perhaps around $6. This difference reflects the anticipated reduction in stock price appreciation due to the dividend payout. This adjustment is essential for investors employing strategies like covered calls, where understanding the impact of dividends is paramount. Accurate pricing, achieved through the black scholes formula with dividends, is vital for managing risk and maximizing returns in such strategies.
Beyond Continuous Dividends: Handling Discrete Dividends
The dividend-adjusted Black-Scholes formula with dividends, as discussed so far, assumes a continuous dividend yield. However, dividends are often paid at specific times, such as quarterly or annually. These are known as discrete dividends. In such cases, directly applying the continuous dividend yield ‘q’ might not be accurate. A modified approach is required to account for these discrete payments when using the black scholes formula with dividends.
To handle discrete dividends within the Black-Scholes framework, the present value of the expected future dividends must be subtracted from the current stock price before applying the Black-Scholes model. This adjustment reflects the anticipated price drop on the ex-dividend date. The formula for calculating the present value (PV) of discrete dividends is: PV = Σ (D / (1 + r)^t). Here, ‘D’ represents the expected dividend amount at time ‘t’, ‘r’ is the risk-free interest rate, and ‘t’ is the time until the dividend payment. The summation (Σ) accounts for multiple dividend payments before the option’s expiration date. Once the present value of all expected dividends has been calculated, it is subtracted from the current stock price (S) to obtain an adjusted stock price (S’). This adjusted stock price (S’) is then used in the standard Black-Scholes formula. This alteration to the black scholes formula with dividends, provides a more precise option valuation when dividends are not paid continuously.
For instance, imagine a stock trading at $50 is expected to pay a $1 dividend in one month and another $1 dividend in three months. Assume a risk-free rate of 5% per year. The present value of the first dividend is $1 / (1 + 0.05/12)^1 ≈ $0.9959. The present value of the second dividend is $1 / (1 + 0.05/12)^3 ≈ $0.9876. The total present value of dividends is approximately $0.9959 + $0.9876 = $1.9835. The adjusted stock price (S’) would then be $50 – $1.9835 = $48.0165. This adjusted stock price is then used in the black scholes formula with dividends, providing a more accurate option value than using the unadjusted stock price. This method offers a refined valuation by acknowledging the precise timing and amounts of dividend distributions, ultimately enhancing the precision of the black scholes formula with dividends.
Limitations and Considerations of the Dividend-Adjusted Model
The dividend-adjusted Black-Scholes formula with dividends provides a valuable framework for estimating option prices on dividend-paying assets, it is essential to recognize its inherent limitations. The standard model relies on several assumptions that may not always hold true in real-world scenarios. One crucial assumption is that the volatility of the underlying asset remains constant throughout the option’s life. In reality, volatility can fluctuate significantly due to market events, economic news, and company-specific announcements. This deviation from constant volatility can impact the accuracy of the option price calculated using the Black-Scholes formula with dividends.
Another key assumption involves the risk-free interest rate, which is also assumed to be constant. Changes in monetary policy or economic conditions can cause interest rates to vary, affecting the present value calculations within the model. Furthermore, the dividend yield itself is assumed to be constant and known with certainty. However, companies can change their dividend policies at any time, increasing, decreasing, or even suspending dividend payments altogether. Predicting future dividend payments accurately is a challenge, making the dividend-adjusted Black-Scholes formula with dividends an approximation rather than a precise determination of fair value. The continuous dividend model assumes that the dividends are paid continuously throughout the option’s life, which is rarely the case. Most companies pay dividends quarterly, semi-annually, or annually. The black scholes formula with dividends provides a more accurate reflection of an option’s fair value than its non-adjusted counterpart, one must understand it’s subject to real-world conditions.
The dividend-adjusted Black-Scholes formula with dividends also doesn’t account for early exercise of American options. This is particularly important for put options on dividend-paying stocks, as it may be optimal to exercise the put option early to capture the dividend payment. These limitations highlight the importance of using the dividend-adjusted Black-Scholes formula with dividends as a tool in conjunction with other valuation methods and considering market conditions. Keep in mind that accurate option pricing also relies heavily on reliable input data. Even with adjustments, the black scholes formula with dividends should be viewed as a guide rather than a definitive price predictor.
Practical Application: Leveraging Dividend-Adjusted Option Pricing
The dividend-adjusted black scholes formula with dividends becomes a valuable tool for investors and traders. It enhances decision-making within the options market, particularly when dealing with dividend-paying stocks. One practical application lies in covered call strategies. Investors holding dividend-paying stocks can sell call options to generate income. The dividend-adjusted black scholes formula with dividends helps them assess a fair premium for these options, considering the expected dividend payments. This ensures they are adequately compensated for potentially giving up the stock’s upside potential before the dividend is paid.
Options can also be strategically employed to hedge against dividend risk. If an investor anticipates a potential decrease in a stock’s price following a dividend payment (due to the ex-dividend date effect), they might purchase put options. By utilizing the dividend-adjusted black scholes formula with dividends, the investor can more accurately determine the appropriate strike price and premium for the put options, effectively protecting their investment from the anticipated price decline. Furthermore, arbitrage opportunities may arise from discrepancies between the theoretical option price derived from the dividend-adjusted model and the actual market price. Sophisticated traders can exploit these differences for profit, although such opportunities are often short-lived and require precise execution.
The key takeaway is that incorporating the dividend adjustment into the standard black scholes formula with dividends leads to more precise option pricing. This increased accuracy translates into better-informed trading decisions, improved risk management, and the potential for enhanced returns when dealing with options on dividend-paying assets. By understanding and applying this modified formula, market participants gain a significant advantage in navigating the complexities of the options market. Always remember that while the black scholes formula with dividends provides a valuable framework, it is crucial to also consider other factors, such as market sentiment and liquidity, when making investment decisions.