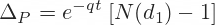Black Scholes Formula for Put Option

Unlocking the Secrets of Put Option Pricing

Put options are a vital tool in the world of investing. They grant the holder the right, but not the obligation, to sell an underlying asset at a predetermined price (the strike price) before a specified date (the expiration date). Accurately pricing these options is paramount for effective risk management. It also creates opportunities for profit. Understanding the factors that influence put option prices is the first step. This article will explore how to decipher the fair value of put options, focusing on the widely used Black Scholes formula for put option. Mastering the Black Scholes formula for put option provides insights into potential market movements and informed investment decisions.

Several elements influence the price of a put option. The current market price of the underlying asset is a primary driver. A lower stock price generally increases the value of a put option, as it becomes more profitable to sell at the higher strike price. The strike price itself is crucial; the higher the strike price relative to the stock price, the more valuable the put option. Time to expiration also plays a significant role. The longer the time until expiration, the greater the chance for the asset price to decline, increasing the option’s value. The risk-free interest rate also has a minor influence. However, volatility is arguably the most critical factor, where implied volatility is the market’s expectation of future price fluctuations.

The Black Scholes formula for put option is a mathematical model designed to estimate the theoretical price of a put option. It considers all the factors mentioned above. While the Black Scholes formula for put option isn’t perfect due to its underlying assumptions, it offers a valuable framework for understanding option pricing. Its widespread use makes it a standard benchmark in the financial industry. By understanding the intricacies of the Black Scholes formula for put option, investors can gain a competitive edge and make more informed decisions when trading or hedging with put options.

Gaining a Clear Understanding of Option Pricing Models

Option pricing models serve a crucial function in the financial world: estimating the theoretical value of options contracts. While no model can perfectly predict the future, these models offer a structured framework for analysis, aiding investors in making informed decisions. The aim is to determine whether an option’s market price is fair relative to its intrinsic characteristics and prevailing market conditions. This process involves analyzing several factors that influence option prices, ultimately helping investors assess potential risks and rewards. Understanding the principles behind these models is essential for anyone involved in options trading or risk management.

Among the various option pricing models, the Black-Scholes model is a cornerstone of financial theory. While alternatives exist, such as the binomial model, the Black-Scholes model stands out for its elegance and computational efficiency. The binomial model, for example, uses an iterative procedure, allowing for the specification of nodes, and is useful for American options. The Black-Scholes model, however, uses a closed-form equation, providing a quicker calculation of the theoretical price of European-style options. For the purpose of this article, we will focus on the Black-Scholes formula for put option, a widely used and influential model that provides a valuable benchmark for understanding option valuation. The following sections will provide a detailed, easy-to-understand breakdown of the Black-Scholes formula for put options.

The decision to concentrate on the Black-Scholes model stems from its balance of accuracy and simplicity. This model relies on key inputs, including the underlying asset’s price, the option’s strike price, the time remaining until expiration, the risk-free interest rate, and the volatility of the underlying asset. Understanding how each of these factors influences the option price is crucial for effective utilization of the model. By focusing on the Black-Scholes formula for put option, this article seeks to provide a practical guide for investors looking to enhance their understanding of option pricing and risk management. In subsequent sections, this article will show how to apply the Black-Scholes formula for put option, using readily available online calculators and real-world examples to demonstrate the model’s application and potential discrepancies. An understanding of the Black-Scholes formula for put option provides a solid foundation for evaluating put option prices and implementing effective trading strategies.

How to Calculate Put Option Value: A Step-by-Step Guide

This section provides a detailed, easy-to-understand breakdown of how to calculate the value of a put option using the black scholes formula for put option. The black scholes formula for put option offers a theoretical price. Each variable is defined clearly to understand its impact on the put option price.

The Black-Scholes formula for put options is:
P = Xe^-rTN(-d₂) – S₀N(-d₁)
Where:

• P = Put option price
• S₀ = Current stock price
• X = Strike price
• T = Time to expiration (in years)
• r = Risk-free interest rate
• e = The exponential constant (approximately 2.71828)
• N(x) = Cumulative standard normal distribution function
• d₁ = [ln(S₀/X) + (r + (σ²/2))T] / (σ√T)
• d₂ = d₁ – σ√T
• σ = Volatility of the stock

Let’s break down each variable:

• Stock Price (S₀): The current market price of the underlying asset. A higher stock price generally decreases the put option value.
• Strike Price (X): The price at which the asset can be sold when exercising the option. A higher strike price generally increases the put option value.
• Time to Expiration (T): The time remaining until the option expires, expressed in years. A longer time to expiration generally increases the put option value, as there is more opportunity for the stock price to move.
• Risk-Free Interest Rate (r): The rate of return on a risk-free investment, such as a U.S. Treasury bond. A higher risk-free interest rate generally decreases the put option value.
• Volatility (σ): A measure of how much the stock price is expected to fluctuate. Higher volatility generally increases the put option price.

To use the black scholes formula for put option, you’ll need to calculate d₁ and d₂ first. Then, find the cumulative standard normal distribution function N(d₁) and N(d₂). These values can be found using statistical tables or readily available online calculators. Input all the values into the formula. Modern calculators and websites offer Black-Scholes calculators. These tools simplify the process.
For example, consider a stock trading at $100 (S₀). The put option has a strike price of $105 (X). It expires in 0.5 years (T). The risk-free interest rate is 5% (r = 0.05). The volatility is 20% (σ = 0.20). By inputting these values into the black scholes formula for put option, you can determine the theoretical put option price. You will be able to determine the theoretical price, by using either an online calculator or doing it by hand. This example shows how the black scholes formula for put option works.

The Intricacies of Volatility in Option Valuation

Volatility is a critical element within the Black-Scholes formula for put option calculations and understanding its nuances is essential. It represents the degree of price fluctuation of the underlying asset over a specific period. Unlike other inputs that are readily available, such as stock price or interest rates, volatility is often an estimation, making it a significant factor influencing the accuracy of the Black-Scholes formula for put option pricing.

There are primarily two types of volatility to consider: historical and implied. Historical volatility looks at past price movements to gauge future potential fluctuations. It’s a backward-looking measure. Implied volatility, on the other hand, is derived from the market price of the option itself. It reflects the market’s expectation of future volatility until the option’s expiration date. The VIX index, often referred to as the “fear gauge,” is a popular measure of implied volatility in the S&P 500 index. The Black-Scholes formula for put option benefits from a correct volatility input.

A higher volatility generally results in a higher put option price. This is because increased volatility suggests a greater possibility that the underlying asset’s price will fall significantly. A substantial price decrease would make the put option more valuable, as it gives the holder the right to sell the asset at the higher strike price. Therefore, investors are willing to pay more for a put option when volatility is high, to hedge against potential losses from significant market movements. The relationship between volatility and put option prices is a cornerstone of the Black-Scholes formula for put option applications. Furthermore, it’s important to remember that accurately estimating volatility remains a challenge, and various methods and resources exist to aid in this process, ultimately affecting the output of the black scholes formula for put option calculations.

Delving into the Assumptions and Limitations

The black scholes formula for put option is a cornerstone of options pricing theory, it’s crucial to acknowledge its underlying assumptions and inherent limitations. The model operates on several key assumptions, including constant volatility of the underlying asset, efficient markets where information is immediately reflected in prices, and the absence of dividends during the option’s life. These assumptions, while simplifying the calculation, can lead to deviations between the theoretical price derived from the black scholes formula for put option and the actual market price, especially in volatile market conditions.

One significant limitation of the black scholes formula for put option is its sensitivity to the volatility input. The model assumes that volatility remains constant over the option’s lifespan, which is rarely the case in reality. Market volatility can fluctuate significantly due to various economic and political factors, rendering the model less accurate. Furthermore, the basic black scholes formula for put option does not account for dividend payments. While adjustments can be made to incorporate dividends, these adjustments add complexity and may not fully capture the impact of dividends on option prices. The black scholes formula for put option was originally designed for European-style options, which can only be exercised at expiration. This limits its applicability to American-style options, which can be exercised at any time before expiration. The possibility of early exercise, particularly when dividends are involved, can significantly affect the option’s value, a factor not directly addressed by the basic black scholes formula for put option.

It’s also important to recognize that the black scholes formula for put option assumes a log-normal distribution of asset prices. While this assumption is reasonable for many assets, it may not hold true for assets with skewed or kurtotic return distributions. Extreme events, or “fat tails,” are more common in reality than predicted by a normal distribution, which can lead to underpricing of options, particularly out-of-the-money puts. Despite these limitations, the black scholes formula for put option remains a valuable tool for understanding the factors that influence option prices. By acknowledging the model’s assumptions and limitations, investors can use it judiciously and supplement it with other analytical tools and market insights to make more informed decisions. The black scholes formula for put option provides a framework for understanding option pricing, but it should not be the sole basis for investment decisions.

Real-World Examples: Applying the Model to Actual Stocks

To illustrate the practical application of the black scholes formula for put option, consider Apple Inc. (AAPL). As of October 26, 2023, suppose AAPL is trading at $170. An investor is considering purchasing a put option with a strike price of $165 that expires in 3 months (0.25 years). The risk-free interest rate is 4% (0.04), derived from U.S. Treasury yields. Finally, implied volatility for this option, obtained from options data providers, is estimated at 25% (0.25). Plugging these values into a black scholes formula for put option calculator, either online or implemented programmatically, yields a theoretical put option price. The black scholes formula for put option serves as the base to pricing this example.

Using the Black-Scholes model requires calculating d1 and d2, intermediate variables used within the formula. Then, by applying the cumulative standard normal distribution to these values, the theoretical price of the put option can be determined. If, after calculation using the black scholes formula for put option, the theoretical price is $2.50, this suggests that, based on the model’s assumptions, the put option should be fairly priced at this amount. However, the actual market price of the same put option may be $3.00. This difference could be attributed to various factors, such as supply and demand, market sentiment, or differing estimates of volatility. The black scholes formula for put option is very sensitive to volatility.

It’s important to remember that the black scholes formula for put option provides a theoretical value. Discrepancies between the theoretical and actual prices do not automatically indicate an arbitrage opportunity. Transaction costs, bid-ask spreads, and the model’s inherent limitations should all be considered. Furthermore, implied volatility is a forward-looking estimate and can fluctuate significantly. By comparing the calculated price from the black scholes formula for put option with the market price, investors can gain a better understanding of option valuations and make more informed trading decisions. Remember that, while helpful, the black scholes formula for put option is not infallible, and should be used in conjunction with other analysis tools.

Beyond Black-Scholes: Exploring Advanced Strategies

The exploration of option strategies extends far beyond the fundamental understanding of individual put options. The Black-Scholes model serves as a crucial building block for comprehending more sophisticated approaches. Strategies like protective puts and covered calls rely heavily on the principles established by the black scholes formula for put option. A protective put, for instance, involves purchasing a put option on a stock already owned. This offers downside protection, limiting potential losses should the stock price decline. The cost of this protection is the premium paid for the put option, a value estimated using the black scholes formula for put option.

Conversely, a covered call strategy involves selling a call option on a stock holding. This generates income in exchange for potentially limiting upside gains if the stock price rises significantly. While the black scholes formula for put option directly prices puts, its underlying principles of risk and probability are vital for evaluating the potential rewards and risks associated with covered calls. Furthermore, understanding the factors that influence put option prices, as highlighted by the Black-Scholes model (stock price, strike price, time to expiration, risk-free interest rate, volatility), becomes essential for making informed decisions when implementing these more complex strategies.

It is important to recognize that advanced strategies, such as iron condors or butterfly spreads, often involve combinations of both put and call options at multiple strike prices and expiration dates. A solid foundation in the black scholes formula for put option, along with an understanding of volatility and its impact on option prices, is crucial for effectively managing the risks associated with these multi-faceted strategies. Although delving into the specifics of each strategy is beyond the scope, grasping the fundamentals of the black scholes formula for put option provides the bedrock necessary for navigating the complexities of advanced option trading and employing sophisticated risk management techniques.

The Bottom Line: Mastering Put Option Pricing for Informed Decisions

Understanding put option pricing is critical for investors looking to manage risk and capitalize on market movements. The black scholes formula for put option provides a foundational framework for estimating the theoretical value of these instruments. While the black scholes formula for put option has limitations, it remains a valuable tool when used judiciously and with an awareness of its underlying assumptions. Mastering the black scholes formula for put option empowers investors to make more informed decisions about buying, selling, or hedging with put options.

The black scholes formula for put option is not a crystal ball, but rather a sophisticated analytical tool. Its accuracy depends heavily on the inputs used, particularly the volatility estimate. Investors should always supplement the black scholes formula for put option with their own market analysis and due diligence. A deep understanding of the black scholes formula for put option allows for a more nuanced understanding of option strategies and risk management. Recognizing the model’s limitations is as important as understanding its applications.

In conclusion, while the black scholes formula for put option offers a solid foundation, continuous learning and adaptation are key to success in options trading. This model serves as a stepping stone to more advanced strategies and a deeper understanding of market dynamics. Embrace the black scholes formula for put option as one component of a comprehensive investment strategy, always remembering that real-world markets are complex and ever-changing. Further research and study of options pricing are highly recommended for anyone seeking to navigate the world of options with confidence.