What is Average Rate of Return and Why Does it Matter?
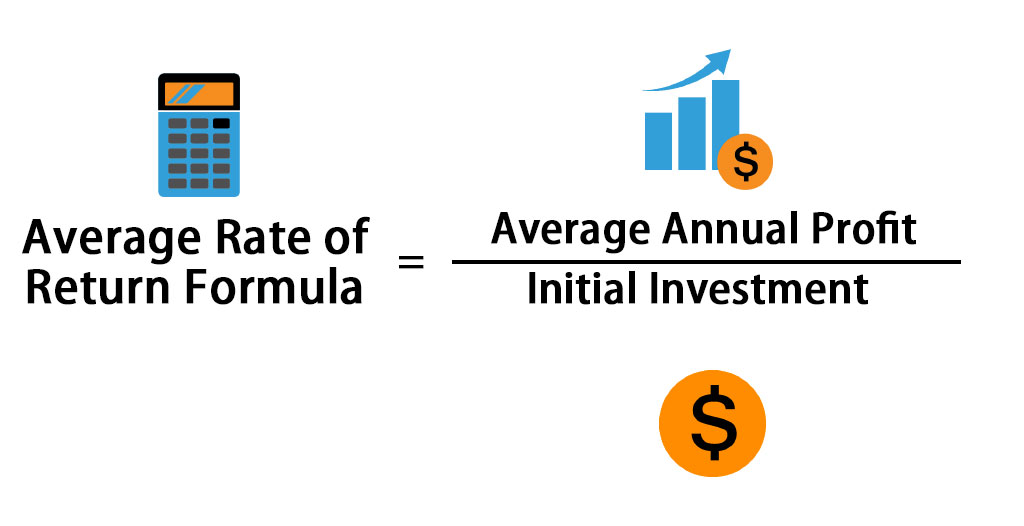
In the world of investments, understanding the average rate of return is crucial for making informed decisions. It’s a fundamental concept that helps investors evaluate the performance of their investments and make data-driven choices. The average rate of return, also known as the arithmetic average rate of return, is a measure of the average return of an investment over a specific period.
The importance of average rate of return lies in its ability to help investors compare different investments and make informed decisions. By knowing the average rate of return, investors can assess the risk and potential return of an investment, making it easier to choose between different options. Moreover, average rate of return is a key metric in portfolio management, as it helps investors optimize their portfolios and achieve their financial goals.
Unlike other return metrics, such as geometric average return, the arithmetic average rate of return provides a simple and intuitive way to evaluate investment performance. It’s a widely used metric in the investment industry, and understanding its calculation and application is essential for any investor.
How to Calculate Average Rate of Return: A Step-by-Step Guide
The arithmetic average rate of return is a crucial metric in investment analysis, and calculating it accurately is essential for informed decision-making. The formula for calculating the arithmetic average rate of return is as follows:
R1 + R2 + … + Rn / n
Where R1, R2, …, Rn are the returns for each period, and n is the number of periods.
To illustrate the application of this formula, let’s consider an example. Suppose an investor wants to calculate the average rate of return for a stock that has returned 10%, 15%, and 20% over the past three years. Using the formula, the calculation would be:
(10% + 15% + 20%) / 3 = 15%
This means that the stock has an arithmetic average rate of return of 15% over the three-year period.
In addition to this simple example, the arithmetic average rate of return can be applied to more complex investment scenarios, such as calculating the return of a portfolio of stocks or bonds. By understanding how to calculate the arithmetic average rate of return, investors can gain valuable insights into the performance of their investments and make more informed decisions.
The Arithmetic Average Rate of Return Formula: Breaking it Down
The arithmetic average rate of return formula, R1 + R2 + … + Rn / n, may seem straightforward, but each component plays a crucial role in the calculation. Understanding the significance of each component is essential for accurate calculations and informed investment decisions.
The returns for each period, R1, R2, …, Rn, are the building blocks of the arithmetic average rate of return formula. These returns can be expressed as a percentage or a decimal value, and they represent the change in value of the investment over a specific period. For example, if a stock returns 10% in a given year, the return for that period would be 0.10.
The number of periods, n, is another critical component of the formula. This value determines the scope of the calculation, with a larger n indicating a longer time frame. For instance, if an investor wants to calculate the arithmetic average rate of return over a five-year period, n would be 5.
The division of the sum of the returns by the number of periods is what gives the arithmetic average rate of return its intuitive appeal. This calculation provides a single value that represents the average performance of the investment over the specified time frame. However, it’s essential to recognize that this value can be influenced by the volatility of the returns, with more volatile investments potentially producing skewed results.
By grasping the intricacies of the arithmetic average rate of return formula, investors can better understand the strengths and limitations of this metric. This knowledge can help investors make more informed decisions, as they can accurately interpret the results of the calculation and adjust their investment strategies accordingly.
Real-World Applications: Using Average Rate of Return in Investment Analysis
In the world of investment analysis, the arithmetic average rate of return is a versatile metric that plays a crucial role in various applications. From evaluating portfolio performance to assessing risk and measuring investment success, the average rate of return is an essential tool for investors and financial professionals.
One of the primary applications of the arithmetic average rate of return is in portfolio evaluation. By calculating the average rate of return for a portfolio, investors can gain insights into its overall performance and make informed decisions about asset allocation. For instance, if a portfolio has an arithmetic average rate of return of 8% over a five-year period, investors may consider it a successful investment.
Risk assessment is another critical application of the average rate of return. By analyzing the average rate of return of different investments, investors can gauge their risk profiles and make informed decisions about asset allocation. For example, if a stock has an arithmetic average rate of return of 12% over a three-year period, but with a high standard deviation, investors may consider it a high-risk investment.
The average rate of return is also used in performance measurement, where it serves as a benchmark for evaluating investment success. By comparing the average rate of return of an investment to a benchmark or industry average, investors can determine whether their investment is performing well or poorly. For instance, if a mutual fund has an arithmetic average rate of return of 10% over a five-year period, but the industry average is 12%, investors may consider it an underperforming investment.
In addition to these applications, the arithmetic average rate of return is also used in other areas of investment analysis, such as investment selection, portfolio rebalancing, and risk management. By understanding how to apply the average rate of return in these contexts, investors can make more informed decisions and achieve their investment goals.
Common Pitfalls to Avoid When Calculating Average Rate of Return
When calculating the arithmetic average rate of return, investors often make mistakes that can lead to inaccurate results. These mistakes can be costly, as they can inform poor investment decisions. To avoid these pitfalls, it’s essential to understand the common errors investors make when calculating the average rate of return.
One of the most common mistakes is ignoring compounding. Compounding occurs when returns are reinvested to generate additional returns. Failing to account for compounding can result in a lower arithmetic average rate of return than the actual return. For example, if an investment returns 10% in year one and 12% in year two, the arithmetic average rate of return would be 11%. However, if the returns are compounded, the actual return would be higher than 11%.
Another mistake is using the wrong time period. The arithmetic average rate of return is sensitive to the time period used in the calculation. Using a shorter or longer time period can significantly impact the result. For instance, if an investment has a high return in a single year, using a short time period may overstate the average rate of return.
Investors also often fail to adjust for inflation. Inflation can erode the purchasing power of returns, making them appear lower than they actually are. To get an accurate picture of the average rate of return, investors must adjust for inflation. For example, if an investment returns 8% in a year with 2% inflation, the real return would be 6%.
To avoid these pitfalls, investors should ensure they use the correct formula, account for compounding, and adjust for inflation. By doing so, they can get an accurate picture of their investment’s performance and make informed decisions.
Comparing Average Rate of Return to Other Investment Metrics
When evaluating investment performance, investors often rely on various metrics to gauge success. The arithmetic average rate of return is one such metric, but it’s essential to understand how it compares to other investment metrics. By doing so, investors can gain a more comprehensive understanding of their investments and make informed decisions.
One commonly used metric is the geometric average return. Unlike the arithmetic average rate of return, which calculates the average return as a simple average, the geometric average return takes into account the compounding effect of returns. This makes it a more accurate representation of investment performance over time. For example, if an investment returns 10%, 12%, and 8% in three consecutive years, the arithmetic average rate of return would be 10%, while the geometric average return would be 9.9%.
Another metric is the internal rate of return (IRR), which calculates the rate of return required to break even on an investment. While the arithmetic average rate of return provides a general idea of investment performance, the IRR offers a more nuanced view of an investment’s profitability. For instance, if an investment has an IRR of 12%, it means that the investment is expected to generate a 12% return to break even.
The strengths of the arithmetic average rate of return lie in its simplicity and ease of calculation. It provides a quick snapshot of investment performance, making it ideal for high-level analysis. However, its limitations include ignoring compounding and being sensitive to extreme values. In contrast, the geometric average return and IRR offer more accurate representations of investment performance, but are more complex to calculate.
Ultimately, investors should use a combination of metrics to gain a comprehensive understanding of their investments. By understanding the strengths and limitations of each metric, investors can make more informed decisions and optimize their investment strategies.
Using Average Rate of Return to Inform Investment Decisions
When it comes to making informed investment decisions, understanding the arithmetic average rate of return is crucial. This metric provides a snapshot of an investment’s performance, allowing investors to evaluate its potential and make data-driven decisions. By incorporating the arithmetic average rate of return into their investment strategy, investors can optimize their portfolios and achieve their financial goals.
One key application of the arithmetic average rate of return is in asset allocation. By comparing the average rate of return of different asset classes, investors can determine the optimal allocation for their portfolio. For example, if an investor finds that stocks have historically provided a higher arithmetic average rate of return than bonds, they may choose to allocate a larger portion of their portfolio to stocks.
The arithmetic average rate of return also plays a critical role in risk management. By evaluating the average rate of return of an investment, investors can assess its risk profile and make informed decisions about its inclusion in their portfolio. For instance, if an investment has a high arithmetic average rate of return but also comes with high volatility, an investor may choose to limit their exposure to mitigate risk.
Furthermore, the arithmetic average rate of return is essential for portfolio rebalancing. As market conditions change, an investor’s portfolio may become misaligned with their target allocation. By regularly reviewing the arithmetic average rate of return of their investments, investors can identify areas that require rebalancing and make adjustments to maintain their target allocation.
Ultimately, the arithmetic average rate of return is a powerful tool for investors. By understanding this metric and incorporating it into their investment strategy, investors can make informed decisions, optimize their portfolios, and achieve their financial goals.
Maximizing Returns: Strategies for Improving Average Rate of Return
Investors seeking to maximize their returns often focus on improving their arithmetic average rate of return. By implementing effective strategies, investors can increase their chances of achieving their financial goals. Here are some actionable strategies for improving average rate of return:
Diversification is a key strategy for improving average rate of return. By spreading investments across different asset classes, sectors, and geographies, investors can reduce risk and increase potential returns. A diversified portfolio can help mitigate losses in one area by offsetting them with gains in another.
Dollar-cost averaging is another effective strategy for improving average rate of return. This involves investing a fixed amount of money at regular intervals, regardless of the market’s performance. By doing so, investors can reduce the impact of market volatility and timing risks, ultimately leading to a higher average rate of return.
Tax-efficient investing is also crucial for maximizing returns. Investors should aim to minimize tax liabilities by allocating investments to tax-advantaged accounts, such as 401(k)s or IRAs. Additionally, investors can consider tax-loss harvesting, which involves selling losing investments to offset gains from winning investments.
Regular portfolio rebalancing is essential for maintaining an optimal asset allocation and improving average rate of return. As market conditions change, an investor’s portfolio may become misaligned with their target allocation. By regularly reviewing and rebalancing their portfolio, investors can ensure that their investments remain aligned with their goals.
Finally, investors should consider adopting a long-term perspective when seeking to improve their average rate of return. By focusing on long-term growth rather than short-term gains, investors can ride out market fluctuations and benefit from the power of compounding.
By incorporating these strategies into their investment approach, investors can improve their arithmetic average rate of return and increase their chances of achieving financial success.

:max_bytes(150000):strip_icc()/RoR-5c61fb1946e0fb0001f25474.jpg)