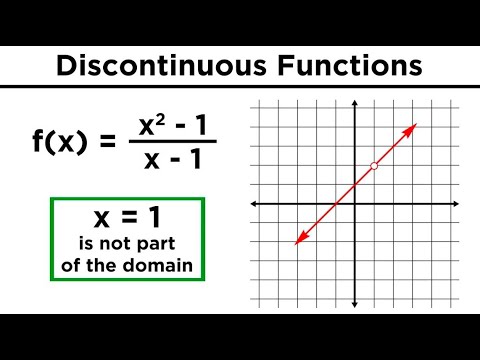
What Makes a Function Continuous?
In mathematics, a function is considered continuous if its graph can be drawn without lifting the pencil from the paper. This means that the function has no gaps, jumps, or asymptotes. In other words, a continuous function is one where the output changes smoothly as the input changes. The concept of limits plays a crucial role in determining the continuity of a function. A function f(x) is said to be continuous at a point x=a if the limit of f(x) as x approaches a exists and is equal to f(a). This can be mathematically represented as lim x→a f(x) = f(a). Understanding the concept of limits is essential in determining the continuity of a function, as it helps to identify any potential discontinuities. For instance, the function f(x) = 1/x is not continuous at x=0 because the limit as x approaches 0 does not exist. On the other hand, the function f(x) = x^2 is continuous at all points because the limit as x approaches any value exists and is equal to the function value. In fact, understanding when a function is continuous but not differentiable is critical in many mathematical and real-world applications.
When Does a Function Fail to be Differentiable?
Differentiability is a fundamental concept in calculus that measures the rate of change of a function with respect to its input. A function is said to be differentiable at a point if its derivative exists at that point. However, not all continuous functions are differentiable. In fact, there are scenarios where a function is continuous but not differentiable. Understanding when a function is continuous but not differentiable is crucial in many mathematical and real-world applications. For instance, a function with a corner or cusp is continuous but not differentiable at that point. This is because the derivative does not exist at the point where the corner or cusp occurs. Visual aids such as graphs and charts can help identify these scenarios. The function f(x) = |x| is a classic example of a continuous but non-differentiable function. It is continuous at x=0, but the derivative does not exist at that point. The importance of limits in determining differentiability cannot be overstated. The limit of the difference quotient as the change in x approaches zero is used to define the derivative. If this limit does not exist, then the function is not differentiable. In the next section, we will explore practical tips and techniques for identifying discontinuities in functions.
How to Identify Functions with Discontinuities
Identifying discontinuities in functions is a crucial step in understanding their behavior. There are several techniques to identify discontinuities, including graphical, tabular, and algebraic methods. Graphical methods involve plotting the function on a graph and visually identifying any gaps, jumps, or asymptotes. For instance, the function f(x) = 1/x has a vertical asymptote at x=0, indicating a discontinuity. Tabular methods involve creating a table of values for the function and looking for any inconsistencies or gaps. Algebraic methods involve manipulating the function algebraically to identify any discontinuities. For example, the function f(x) = |x| has a discontinuity at x=0 because the limit as x approaches 0 from the left is -1, while the limit as x approaches 0 from the right is 1. There are different types of discontinuities, including removable discontinuities, infinite discontinuities, and jump discontinuities. Removable discontinuities occur when the limit exists, but the function is not defined at that point. Infinite discontinuities occur when the limit does not exist, and the function approaches infinity. Jump discontinuities occur when the limit exists, but the function has different values on either side of the discontinuity. Understanding when a function is continuous but not differentiable is essential in identifying these types of discontinuities. By mastering these techniques, readers can develop a deeper understanding of function behavior and identify discontinuities with ease.
The Role of Corners, Cusps, and Vertical Tangents
Corners, cusps, and vertical tangents play a crucial role in determining the differentiability of a function. These features can cause a function to be continuous but not differentiable at a particular point. A corner is a point where the function has a sudden change in direction, resulting in a discontinuity in the derivative. A cusp is a point where the function has a sharp, pointed turn, also resulting in a discontinuity in the derivative. A vertical tangent is a point where the function has a vertical slope, making it impossible to define the derivative. These features can be identified using visual aids such as graphs and charts. For example, the function f(x) = |x| has a corner at x=0, making it continuous but not differentiable at that point. Similarly, the function f(x) = x^(2/3) has a cusp at x=0, making it continuous but not differentiable at that point. Understanding the impact of corners, cusps, and vertical tangents on function differentiability is essential in identifying when a function is continuous but not differentiable. By recognizing these features, readers can develop a deeper understanding of function behavior and identify potential issues with differentiability.
Real-World Applications of Continuous but Non-Differentiable Functions
Continuous but non-differentiable functions have numerous applications in various fields, including physics, engineering, and economics. In physics, these functions are used to model complex phenomena, such as the motion of objects with non-smooth trajectories. For instance, the function describing the distance of a projectile under gravity is continuous but not differentiable at the point where the projectile changes direction. In engineering, continuous but non-differentiable functions are used to model signal processing and control systems. In economics, these functions are used to model economic systems with discontinuous changes, such as stock market crashes. The significance of continuous but non-differentiable functions lies in their ability to model real-world phenomena that do not always follow smooth and continuous patterns. Understanding when a function is continuous but not differentiable is crucial in these applications, as it allows researchers and practitioners to accurately model and analyze complex systems. By recognizing the importance of these functions, readers can gain a deeper appreciation for the role of mathematics in understanding and describing the world around us.
Common Misconceptions About Function Continuity and Differentiability
One of the most common misconceptions about function continuity and differentiability is that they are interchangeable terms. However, this is not the case. A function can be continuous but not differentiable, as seen in the case of the absolute value function. Another misconception is that a function must be differentiable at a point to be continuous at that point. This is also not true, as a function can be continuous at a point without being differentiable at that point. For example, the function f(x) = |x| is continuous at x=0 but not differentiable at that point. It is essential to understand the differences between continuity and differentiability to avoid these misconceptions. When is a function continuous but not differentiable? This question is crucial in understanding the behavior of functions, and the answer lies in the concept of limits and derivatives. By recognizing the differences between continuity and differentiability, readers can gain a deeper understanding of function behavior and avoid common misconceptions. Additionally, it is essential to remember that a function can be continuous but not differentiable, and this concept has significant implications in real-world applications.
Visualizing Function Behavior with Graphs and Charts
Visualizing function behavior is a crucial step in understanding continuity and differentiability. Graphs and charts provide a powerful tool for identifying continuity and differentiability issues, allowing readers to visualize the behavior of functions and identify potential problems. By plotting a function on a graph, readers can quickly identify discontinuities, corners, cusps, and vertical tangents, which can indicate where a function fails to be differentiable. For example, the graph of the absolute value function clearly shows a corner at x=0, indicating that the function is not differentiable at that point. Similarly, the graph of a function with a vertical tangent can reveal where the function is not differentiable. When is a function continuous but not differentiable? Visualizing function behavior can help answer this question by providing a clear and intuitive understanding of function behavior. Additionally, graphs and charts can be used to compare the behavior of different functions, highlighting the differences between continuous and differentiable functions. By mastering the art of visualizing function behavior, readers can gain a deeper understanding of continuity and differentiability, and develop the skills needed to succeed in mathematics, science, and engineering.
Mastering the Art of Function Analysis
Mastering function analysis, including continuity and differentiability, is crucial for success in mathematics, science, and engineering. By understanding the intricacies of function behavior, readers can develop a deeper appreciation for the underlying principles of calculus and its applications. When is a function continuous but not differentiable? This question is at the heart of function analysis, and answering it requires a thorough understanding of limits, derivatives, and function behavior. By recognizing the importance of continuity and differentiability, readers can unlock the secrets of function analysis and gain a competitive edge in their chosen field. To further develop their skills, readers are encouraged to explore advanced topics in calculus, such as infinite series and multivariable calculus, and to apply their knowledge to real-world problems. With persistence and dedication, readers can become proficient in function analysis and unlock the full potential of calculus.