Binomial Lattice Option Pricing Model

Unlocking the Power of Binomial Lattices in Finance

In the world of finance, option pricing models play a vital role in determining the value of complex derivatives. The binomial lattice option pricing model has emerged as a powerful tool for simplifying complex financial calculations and providing accurate results. By discretizing time and assuming that the underlying asset’s price can move up or down at each node, binomial lattices offer a flexible and intuitive approach to option valuation. This approach has gained widespread acceptance in the financial industry due to its ability to handle a wide range of options, including American and European options, as well as exotic options with complex payoff structures. As a result, binomial lattice models have become an essential component of modern finance, enabling investors and financial institutions to make informed decisions in an increasingly complex market landscape. The binomial lattice option pricing model’s ability to provide accurate results and simplify complex financial calculations has made it a go-to tool for finance professionals.

How to Build a Binomial Lattice: A Step-by-Step Approach

Constructing a binomial lattice option pricing model requires a thorough understanding of the underlying principles and a systematic approach. To build a binomial lattice, follow these steps:

Step 1: Select the Parameters – Identify the underlying asset, option type, and relevant market data, including the risk-free rate, volatility, and time to expiration.

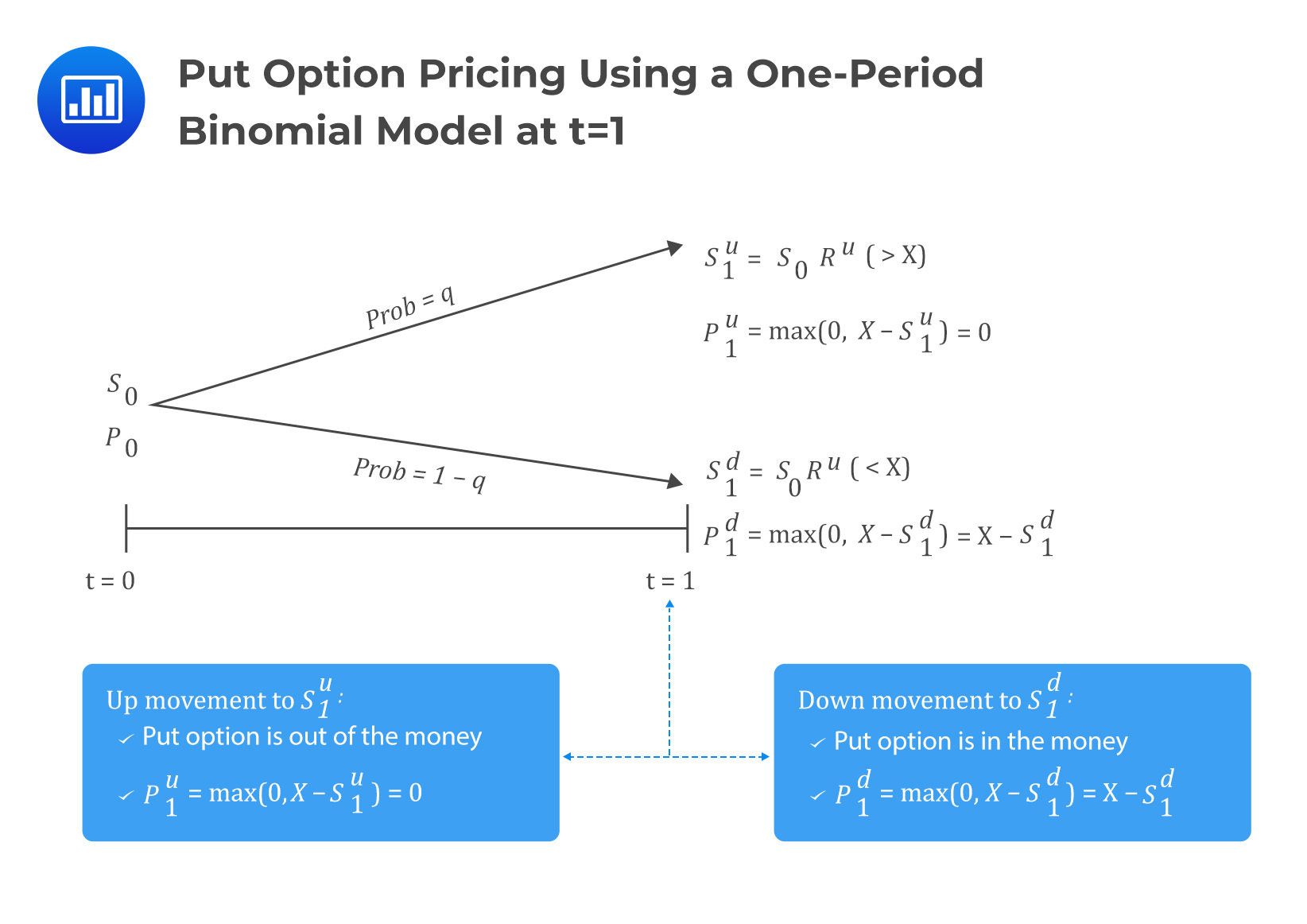
Step 2: Create the Lattice Structure – Discretize time into a series of nodes, with each node representing a possible price movement of the underlying asset. The number of nodes and time steps will depend on the desired level of accuracy and computational complexity.

Step 3: Calculate Probabilities – Determine the probability of an up or down move at each node, using the binomial probability distribution. This will enable the calculation of option values at each node.

Step 4: Value the Option – Starting from the final node, work backwards through the lattice, calculating the option value at each node using the risk-neutral valuation approach. This will ultimately provide the current option value.

By following these steps, a binomial lattice option pricing model can be constructed, providing a powerful tool for option valuation and risk management. The flexibility and accuracy of binomial lattices make them an essential component of modern finance, enabling investors and financial institutions to make informed decisions in an increasingly complex market landscape.

The Mathematics Behind Binomial Lattices: Understanding the Greeks

The binomial lattice option pricing model is built upon a solid mathematical foundation, which enables it to provide accurate results and simplify complex financial calculations. At the heart of this model lies the concept of the Greeks, a set of financial metrics that measure the sensitivity of an option’s value to changes in various underlying factors.

Delta (Δ) represents the rate of change of the option’s value with respect to the underlying asset’s price. It is a crucial metric for risk management, as it helps investors and financial institutions to hedge their positions effectively.

Gamma (Γ) measures the rate of change of the option’s delta, providing insight into the option’s sensitivity to changes in the underlying asset’s price. This metric is essential for managing the risk associated with option positions.

Theta (θ) represents the rate of change of the option’s value with respect to time, highlighting the impact of time decay on option values. This metric is critical for investors and financial institutions seeking to optimize their option strategies.

Vega (ν) measures the rate of change of the option’s value with respect to volatility, providing insight into the option’s sensitivity to changes in market conditions. This metric is vital for managing the risk associated with option positions in volatile markets.

By understanding the Greeks and their role in the binomial lattice option pricing model, investors and financial institutions can make informed decisions, optimize their option strategies, and manage risk more effectively. The mathematical foundations of binomial lattices provide a robust framework for option pricing and risk management, making them an essential tool in modern finance.

Advantages of Binomial Lattices over Other Option Pricing Models

When it comes to option pricing, various models are available, each with its strengths and weaknesses. The binomial lattice option pricing model stands out from other popular models, such as Black-Scholes and finite difference methods, due to its unique advantages.

One of the primary benefits of binomial lattices is their ability to handle complex option pricing problems with ease. By discretizing time and price movements, binomial lattices can accurately value options with multiple underlying assets, dividends, and other features that are difficult to model using other approaches.

In contrast, the Black-Scholes model, although widely used, is limited to European-style options with a single underlying asset and no dividends. Finite difference methods, on the other hand, can be computationally intensive and may require significant computational resources.

Another advantage of binomial lattices is their flexibility in modeling various probability distributions. By allowing for different probability distributions at each node, binomial lattices can capture the nuances of real-world market data, providing more accurate option valuations.

In addition, binomial lattices are well-suited for risk management applications, as they can provide detailed information on the Greeks, enabling investors and financial institutions to hedge their positions effectively.

While other option pricing models, such as Monte Carlo simulations, may be useful for certain applications, binomial lattices offer a unique combination of accuracy, flexibility, and computational efficiency, making them a popular choice among finance professionals.

By understanding the advantages of binomial lattices over other option pricing models, investors and financial institutions can make informed decisions about which model to use for their specific needs, ultimately leading to more effective option pricing and risk management strategies.

Real-World Applications of Binomial Lattices in Finance

Binomial lattice option pricing models have numerous practical applications in finance, making them an essential tool for investors, financial institutions, and corporations. One of the primary uses of binomial lattices is option valuation, where they can accurately price complex options with multiple underlying assets, dividends, and other features.

In risk management, binomial lattices are used to calculate the Greeks, providing valuable insights into the sensitivity of option positions to changes in the underlying asset’s price, volatility, and other factors. This information enables investors and financial institutions to hedge their positions effectively, minimizing potential losses and maximizing gains.

Portfolio optimization is another area where binomial lattices shine. By using binomial lattices to value options and calculate the Greeks, investors can optimize their portfolios to achieve their desired risk-return profiles. This is particularly useful for institutions with large portfolios, where small changes in option values can have a significant impact on overall performance.

In addition to these applications, binomial lattices are also used in capital budgeting, where they help corporations evaluate investment opportunities and make informed decisions about resource allocation. For instance, a company considering a new project can use a binomial lattice option pricing model to value the project’s options and determine the optimal investment strategy.

Real-world examples of binomial lattice applications can be seen in various industries. For instance, a hedge fund may use binomial lattices to value complex options and manage risk, while a corporation may use them to evaluate investment opportunities and optimize its capital structure.

The versatility and accuracy of binomial lattice option pricing models make them an indispensable tool in modern finance, with applications spanning option valuation, risk management, portfolio optimization, and capital budgeting.

Common Challenges and Limitations of Binomial Lattices

While binomial lattice option pricing models offer numerous advantages, they are not without their challenges and limitations. One of the primary concerns is model risk, which arises from the simplifying assumptions made in the binomial lattice framework. These assumptions can lead to inaccuracies in option valuation and risk management, particularly in complex market scenarios.

Another challenge is computational complexity, which can increase exponentially with the number of time steps and underlying assets. This can make binomial lattice models computationally intensive, requiring significant resources and processing power.

Parameter estimation is another limitation of binomial lattices. The accuracy of the model relies heavily on the estimation of parameters such as volatility, interest rates, and dividend yields. Inaccurate parameter estimates can lead to poor option valuations and risk management decisions.

To mitigate these issues, it is essential to carefully select the binomial lattice parameters, ensuring that they accurately reflect the underlying market dynamics. Additionally, implementing robust model validation and testing procedures can help identify and address potential model risks.

Furthermore, combining binomial lattice models with other option pricing approaches, such as finite difference methods or Monte Carlo simulations, can provide a more comprehensive understanding of option values and risks. This hybrid approach can help mitigate the limitations of individual models and provide more accurate results.

By understanding the common challenges and limitations of binomial lattices, finance professionals can take steps to address these issues and ensure that their binomial lattice option pricing models provide accurate and reliable results.

Best Practices for Implementing Binomial Lattices in Financial Modeling

When implementing binomial lattice option pricing models in financial modeling, it is essential to follow best practices to ensure accurate and reliable results. One of the critical steps is data preparation, which involves collecting and cleaning relevant data on the underlying asset, including historical prices, volatility, and dividend yields.

Model calibration is another crucial aspect of implementing binomial lattices. This involves estimating the model parameters, such as the risk-neutral probability and volatility, to ensure that the model accurately reflects the underlying market dynamics. Calibration techniques, such as least-squares optimization, can be used to estimate these parameters.

Result interpretation is also vital when working with binomial lattice models. This involves analyzing the output of the model, including the option values and Greeks, to gain insights into the underlying risks and opportunities. It is essential to understand the limitations of the model and to consider multiple scenarios to ensure robust decision-making.

In addition to these best practices, it is also important to consider the computational efficiency of the binomial lattice model. This can be achieved by using optimized algorithms and parallel processing techniques, which can significantly reduce the computational time and improve the overall performance of the model.

Furthermore, incorporating sensitivity analysis and stress testing into the implementation of binomial lattices can provide valuable insights into the robustness of the model and its ability to handle extreme market scenarios. This can help identify potential weaknesses in the model and improve its overall performance.

By following these best practices, finance professionals can ensure that their binomial lattice option pricing models provide accurate and reliable results, enabling them to make informed investment decisions and manage risk effectively.

Ultimately, the successful implementation of binomial lattices in financial modeling requires a deep understanding of the underlying mathematics and a careful consideration of the model’s limitations and potential pitfalls. By following these guidelines and staying up-to-date with the latest research and innovations, finance professionals can unlock the full potential of binomial lattice option pricing models and achieve their investment objectives.

The Future of Binomial Lattices in Finance: Trends and Innovations

The binomial lattice option pricing model has been a cornerstone of finance for decades, providing a powerful tool for option valuation and risk management. As the finance industry continues to evolve, researchers and practitioners are exploring new ways to improve and extend the capabilities of binomial lattices.

One of the most promising trends in binomial lattice research is the integration of machine learning and artificial intelligence (AI). By combining the strengths of binomial lattices with the power of machine learning algorithms, researchers are developing more accurate and efficient option pricing models. For example, AI-powered binomial lattices can be used to estimate complex volatility surfaces and improve the accuracy of option valuations.

Another area of innovation is the development of hybrid binomial lattice models that combine the strengths of different option pricing approaches. For instance, researchers are exploring the use of binomial lattices in conjunction with finite difference methods to create more robust and flexible option pricing models.

The increasing availability of large datasets and advances in computational power are also driving innovation in binomial lattice research. Researchers are using these resources to develop more complex and realistic binomial lattice models that can handle large datasets and provide more accurate results.

In addition, the growing importance of sustainability and environmental, social, and governance (ESG) considerations in finance is leading to new applications of binomial lattices. For example, researchers are using binomial lattices to value options on ESG-themed assets and to assess the impact of climate change on financial markets.

As the finance industry continues to evolve, it is likely that binomial lattices will remain a key tool for option valuation and risk management. However, the integration of machine learning, AI, and other innovations will likely transform the way binomial lattices are used and improve their accuracy and efficiency.

Ultimately, the future of binomial lattices in finance is bright, with ongoing research and innovation set to unlock new possibilities for option pricing and risk management. As the industry continues to evolve, it is essential for finance professionals to stay up-to-date with the latest developments and trends in binomial lattice research.