Introduction to Proximal Policy Optimization (PPO) Algorithms
Proximal Policy Optimization (PPO) algorithms are a type of reinforcement learning algorithm that offers a balance between sample complexity and ease of implementation. Reinforcement learning is a subfield of machine learning that deals with agents learning to make decisions in an environment to maximize a reward signal. PPO algorithms are designed to address some of the challenges faced by traditional reinforcement learning algorithms, such as the need for a large number of samples and the difficulty of tuning hyperparameters.
At a high level, PPO algorithms aim to optimize a policy function that maps states to actions, with the goal of maximizing the expected cumulative reward. This is in contrast to value-based methods, which instead learn a value function that estimates the expected cumulative reward of a given state or state-action pair. PPO algorithms are considered policy optimization methods, as they directly optimize the policy function.
PPO algorithms differ from other policy optimization methods, such as vanilla policy gradient or natural policy gradient, in that they use a surrogate objective function that includes a constraint on the size of policy updates. This constraint helps to ensure that the new policy does not deviate too much from the old policy, which can help to prevent large policy updates that may result in instability or poor performance. By balancing exploration and exploitation, PPO algorithms can achieve stable and efficient learning, making them a popular choice for reinforcement learning applications.

Key Concepts and Terminology in PPO Algorithms
Proximal Policy Optimization (PPO) algorithms are a type of reinforcement learning algorithm that use a surrogate objective function to optimize a policy function. The policy function maps states to actions, and the goal is to find the policy that maximizes the expected cumulative reward. To understand PPO algorithms, it is important to define and explain some key concepts and terminology.
- Policy Function: The policy function is a mapping from states to actions that the agent uses to decide which action to take in a given state. In PPO algorithms, the policy function is typically represented by a neural network that takes the state as input and outputs a probability distribution over possible actions.
- Value Function: The value function estimates the expected cumulative reward of a given state or state-action pair. In PPO algorithms, the value function is typically represented by a separate neural network that takes the state or state-action pair as input and outputs a scalar value.
- Advantage Function: The advantage function measures the advantage of taking a particular action in a given state, compared to the average action for that state. The advantage function is defined as the difference between the value function and the state-value function. In PPO algorithms, the advantage function is used to update the policy function, as it provides a measure of how much better or worse an action is compared to the average action.
- Surrogate Objective Function: The surrogate objective function is a function that is used to approximate the true objective function. In PPO algorithms, the surrogate objective function is designed to be close to the true objective function, but with a constraint on the size of policy updates. This constraint helps to ensure that the new policy does not deviate too much from the old policy, which can help to prevent large policy updates that may result in instability or poor performance.
By using a surrogate objective function with a constraint on the size of policy updates, PPO algorithms can achieve stable and efficient learning. This is in contrast to traditional policy gradient methods, which can suffer from high variance and instability due to large policy updates. By using the advantage function to update the policy function, PPO algorithms can also achieve better sample efficiency and convergence properties compared to traditional value-based methods.
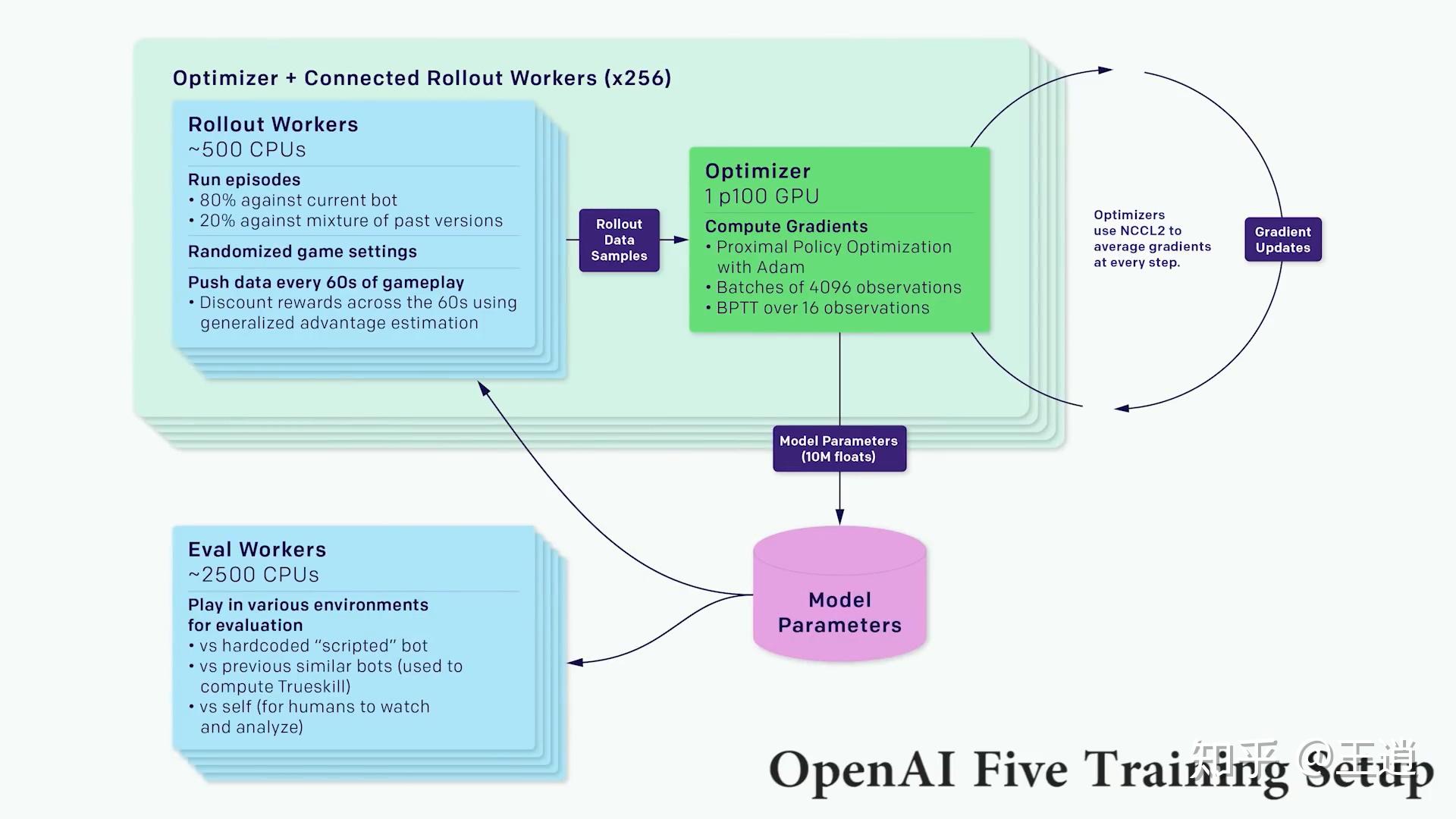
How PPO Algorithms Improve Reinforcement Learning
Proximal Policy Optimization (PPO) algorithms are a type of reinforcement learning algorithm that offer several advantages over traditional methods. One of the key ways that PPO algorithms improve reinforcement learning is by balancing exploration and exploitation, and reducing the risk of large policy updates.
- Balancing Exploration and Exploitation: In reinforcement learning, there is a trade-off between exploration and exploitation. Exploration involves trying out new actions to see if they result in higher rewards, while exploitation involves choosing the actions that have been found to result in the highest rewards so far. PPO algorithms balance these two competing objectives by using a surrogate objective function that encourages the agent to take actions that are likely to result in higher rewards, while also discouraging large policy updates that may result in instability or poor performance. This helps to ensure that the agent continues to explore the environment, while also exploiting the knowledge it has gained so far.
- Reducing the Risk of Large Policy Updates: Traditional policy gradient methods can suffer from high variance and instability due to large policy updates. PPO algorithms address this issue by using a surrogate objective function with a constraint on the size of policy updates. This constraint helps to ensure that the new policy does not deviate too much from the old policy, which can help to prevent large policy updates that may result in instability or poor performance. By reducing the risk of large policy updates, PPO algorithms can achieve more stable and efficient learning.
PPO algorithms also improve reinforcement learning by providing better sample efficiency and convergence properties compared to traditional value-based methods. By using the advantage function to update the policy function, PPO algorithms can achieve better sample efficiency, as they can learn from fewer samples. PPO algorithms can also achieve better convergence properties, as they can avoid getting stuck in local optima that may be suboptimal for the true objective. This can help to ensure that the agent continues to learn and improve over time.
Applications of PPO Algorithms
Proximal Policy Optimization (PPO) algorithms have a wide range of applications in various fields, including robotics, gaming, and autonomous systems. PPO algorithms have been shown to be effective in solving complex reinforcement learning problems, and their ability to balance exploration and exploitation makes them well-suited for real-world applications.
- Robotics: PPO algorithms have been used in robotics to train robots to perform complex tasks, such as grasping objects or navigating environments. By using PPO algorithms, robots can learn to perform these tasks more efficiently and effectively, as they can balance exploration and exploitation to find the best actions to take. PPO algorithms have also been used to train robots to learn from human feedback, which can help to improve their performance and adaptability.
- Gaming: PPO algorithms have been used in gaming to train agents to play complex games, such as Go or Starcraft. By using PPO algorithms, agents can learn to play these games more efficiently and effectively, as they can balance exploration and exploitation to find the best actions to take. PPO algorithms have also been used to train agents to learn from human feedback, which can help to improve their performance and adaptability.
- Autonomous Systems: PPO algorithms have been used in autonomous systems to train vehicles to navigate roads or drones to fly through obstacles. By using PPO algorithms, autonomous systems can learn to perform these tasks more efficiently and effectively, as they can balance exploration and exploitation to find the best actions to take. PPO algorithms have also been used to train autonomous systems to learn from human feedback, which can help to improve their performance and adaptability.
PPO algorithms have also been used in other applications, such as natural language processing, finance, and healthcare. By using PPO algorithms, these applications can learn to perform complex tasks more efficiently and effectively, as they can balance exploration and exploitation to find the best actions to take. PPO algorithms have also been used to train models to learn from human feedback, which can help to improve their performance and adaptability.

Proximal Policy Optimization Algorithms: A Practical Implementation
Implementing Proximal Policy Optimization (PPO) algorithms can be a complex task, but by following a step-by-step guide, it can be made easier. Here is a guide to implementing PPO algorithms, including code examples and best practices.
Step 1: Define the Environment
The first step in implementing PPO algorithms is to define the environment. This can be done using a library such as OpenAI Gym, which provides a wide range of environments to choose from. Once the environment is defined, it is important to normalize the observations and rewards to improve the stability and performance of the algorithm.
Step 2: Define the Policy and Value Functions
The next step is to define the policy and value functions. The policy function is used to determine the probability distribution over the actions given the current state, while the value function is used to estimate the expected return of the current state. In PPO algorithms, both the policy and value functions are typically represented by neural networks.
Step 3: Collect Data
Once the policy and value functions are defined, the next step is to collect data by running the policy in the environment. This data is used to train the policy and value functions using the PPO algorithm.
Step 4: Train the Policy and Value Functions
The next step is to train the policy and value functions using the PPO algorithm. This involves computing the loss function and updating the parameters of the neural networks using gradient descent. It is important to use a suitable optimizer, such as Adam or RMSProp, and to monitor the training process to ensure that it is converging.
Step 5: Evaluate the Policy
Once the policy and value functions have been trained, the next step is to evaluate the policy by running it in the environment and computing the average return. It is important to compare the performance of the new policy to the old policy to ensure that it is improving.
Best Practices
- Use a suitable learning rate and batch size to ensure stable and efficient training.
- Monitor the training process to ensure that it is converging and not diverging.
- Use early stopping to prevent overfitting.
- Use a suitable neural network architecture, such as a multi-layer perceptron or a convolutional neural network.
- Use a suitable activation function, such as ReLU or tanh.
Code Example
Here is an example of how to implement PPO algorithms in Python using TensorFlow:
import tensorflow as tf import gym
Define the environment
env = gym.make("CartPole-v0")
Define the policy and value functions
policy = tf.keras.Sequential([
tf.keras.layers.Dense(64, activation=tf.nn.relu, input_shape=(env.observation_space.shape
0
,)),
tf.keras.layers.Dense(64, activation=tf.nn.relu),
tf.keras.layers.Dense(env.action_space.n, activation=tf.nn.softmax)
])
value = tf.keras.Sequential([
tf.keras.layers.Dense(64, activation=tf.nn.relu, input_shape=(env.observation_space.shape
0
,)),
tf.keras.layers.Dense(64, activation=tf.nn.relu),
tf.keras.layers.Dense(1)
])
Define the loss function
def loss_fn(policy, value, observations, actions, rewards, next_observations, dones):
policy_loss = -tf.reduce_mean(tf.math.log(policy(observations)) * rewards)
value_loss = tf.reduce_mean(tf.square(value(observations) - rewards))
return policy_loss + value_loss
Define the optimizer
optimizer = tf.keras.optimizers.Adam(learning_rate=0.001)
Collect data
observations, actions, rewards, next_observations, dones = [], [], [], [], []
state = env.reset()
for i in range(1000):
action = policy(tf.convert_to_tensor([state]))
next_state, reward, done, _ = env.step(action.numpy()
0
)
observations.append(tf.convert_to_tensor([state]))
actions.append(tf.convert_to_tensor([[action.numpy()
0
]]))
rewards.append(tf.convert_to_tensor([[reward]]))
next_observations.append(tf.convert_to_tensor([next_state]))
dones.append(tf.convert_to_tensor([[done]]))
state = next_state
Train the policy and value functions
with tf.GradientTape() as tape:
loss = loss_fn(policy, value, tf.stack(observations), tf.stack(actions), tf.stack(rewards), tf.stack(next_observations), tf.stack(dones))
gradients = tape.gradient(loss, policy.trainable_variables + value.trainable_variables)
optimizer.apply_gradients(zip(gradients, policy.trainable_variables + value.trainable_variables))
Evaluate the policy
state = env.reset()
total_reward = 0
for i in range(1000):
action = policy(tf.convert_to_tensor([state]))
next_state, reward, done, _ = env.step(action.numpy()
0
)
total_reward += reward
state = next_state
print("Total reward:", total_reward)
By following this guide and using best practices, it is possible to implement PPO algorithms effectively and efficiently. However, it is important to note that PPO algorithms can be sensitive to hyperparameters and computational requirements, which can be challenging to optimize.
Comparing PPO Algorithms to Other Reinforcement Learning Algorithms
Proximal Policy Optimization (PPO) algorithms are a class of reinforcement learning methods that have gained popularity due to their stability and ease of implementation. Compared to other reinforcement learning algorithms, such as Q-learning and Deep Deterministic Policy Gradients (DDPG), PPO algorithms offer several advantages and disadvantages. Understanding these differences is crucial for selecting the appropriate algorithm for a given problem.
PPO vs. Q-learning
Q-learning is a value-based reinforcement learning algorithm that approximates the action-value function, which represents the expected return for taking a specific action in a given state. In contrast, PPO algorithms are policy-based methods that directly optimize the policy function to maximize the expected return. While Q-learning can be more sample-efficient than policy-based methods in some cases, it suffers from challenges such as function approximation errors and the need for careful tuning of the exploration-exploitation trade-off.
PPO algorithms, on the other hand, offer a more stable learning process by using a surrogate objective function that penalizes large policy updates. This approach helps maintain the performance of the current policy while exploring new policies, reducing the risk of catastrophic forgetting. Additionally, PPO algorithms can handle continuous action spaces more effectively than Q-learning, making them suitable for a wider range of applications.
PPO vs. DDPG
Deep Deterministic Policy Gradients (DDPG) is an actor-critic method that combines the benefits of value-based and policy-based approaches. DDPG uses two neural networks, an actor network to approximate the policy function and a critic network to estimate the action-value function. This dual-network architecture allows DDPG to handle continuous action spaces and maintain a balance between exploration and exploitation.
However, DDPG can be sensitive to hyperparameter tuning and prone to instability due to the correlation between the actor and critic networks’ updates. PPO algorithms address these issues by using a clipped surrogate objective function that discourages large policy updates and a multiple-epoch training process that reduces the correlation between policy and value function updates. As a result, PPO algorithms can achieve comparable or even better performance than DDPG in various applications while being more robust and easier to tune.
In summary, PPO algorithms offer several advantages over other reinforcement learning methods, such as stability, ease of implementation, and robustness to hyperparameter tuning. However, they may require more samples than Q-learning in some cases and may not be as sample-efficient as other actor-critic methods like DDPG in certain scenarios. Careful consideration of the problem’s characteristics and the algorithm’s strengths and weaknesses is essential for selecting the most appropriate reinforcement learning method.

