Why Measuring Return Dispersion Matters
Investment risk is an inherent aspect of the financial world. Understanding the potential variability of investment returns is crucial for investors. It allows them to make informed decisions. This article delves into methods for gauging this variability. One vital measure is the ‘standard deviation of a return’. It helps quantify the dispersion of returns around their average. Return dispersion, essentially a synonym for the ‘standard deviation of a return’, indicates the degree to which individual returns deviate from the mean return. A higher ‘standard deviation of a return’ signifies greater volatility. This means a wider range of potential outcomes, both positive and negative. Conversely, a lower ‘standard deviation of a return’ suggests more stable and predictable returns.
Investors need to understand their risk tolerance. It’s the level of volatility they are comfortable with. Different investors may react differently to the same investment. An investor with a high-risk tolerance might seek investments with potentially high returns, even if they come with a higher ‘standard deviation of a return’. Another investor with a low-risk tolerance might prefer investments with lower potential returns but also a lower ‘standard deviation of a return’. Failing to account for the possible range of returns can lead to poor decision-making.
Therefore, grasping the concept of ‘standard deviation of a return’, or return dispersion, becomes essential. It is a tool for assessing potential losses. It also enables investors to align their investment choices with their risk tolerance. This measure helps set realistic expectations. It also aids in constructing portfolios that balance risk and reward. By understanding the ‘standard deviation of a return,’ investors can navigate the complexities of the market. They can also work towards achieving their financial goals with greater confidence. Ignoring this crucial metric can lead to unexpected outcomes and hinder long-term success.
A Simple Guide to Calculate Return Deviation
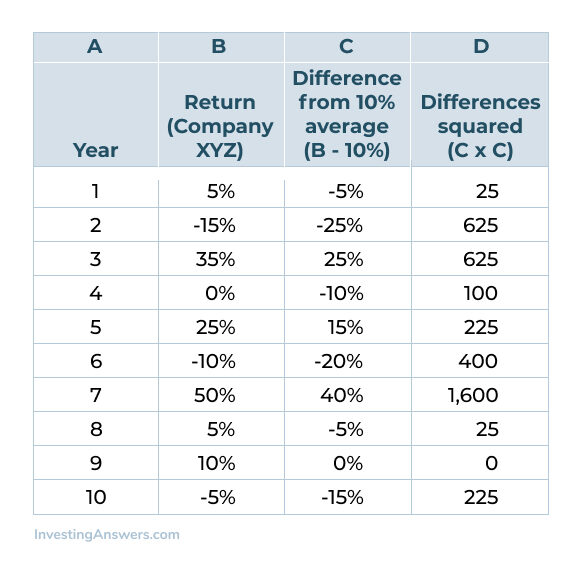
Calculating the ‘standard deviation of a return,’ or ‘return deviation,’ is a fundamental skill for investors seeking to understand the risk associated with an investment. This section provides a step-by-step guide to manually calculating the ‘standard deviation of a return’ using example data. This ‘return deviation’ calculation allows for synonymous ranking purposes and a clear understanding of return variability.
First, gather the historical return data for the investment. For example, let’s say we have the following monthly returns for a stock over the past year: 2%, -1%, 3%, 0%, 1%, -2%, 4%, -3%, 2%, 1%, 0%, -1%. Next, calculate the average return. In this example, the average return is (2 – 1 + 3 + 0 + 1 – 2 + 4 – 3 + 2 + 1 + 0 – 1) / 12 = 0.5%. Now, for each return, calculate the difference between the return and the average return. These differences are: 1.5%, -1.5%, 2.5%, -0.5%, 0.5%, -2.5%, 3.5%, -3.5%, 1.5%, 0.5%, -0.5%, -1.5%. Square each of these differences: 2.25%, 2.25%, 6.25%, 0.25%, 0.25%, 6.25%, 12.25%, 12.25%, 2.25%, 0.25%, 0.25%, 2.25%. Calculate the average of these squared differences, which is (2.25 + 2.25 + 6.25 + 0.25 + 0.25 + 6.25 + 12.25 + 12.25 + 2.25 + 0.25 + 0.25 + 2.25) / 12 = 4.0%. Finally, take the square root of the average squared difference. This gives us the ‘standard deviation of a return’: √4.0% = 2.0%. This means that the ‘standard deviation of a return’ is 2.0%.
This calculation shows that, on average, the monthly returns deviate from the average return by 2.0%. A higher ‘standard deviation of a return’ indicates greater volatility, while a lower value suggests more stable returns. Understanding how to calculate the ‘standard deviation of a return’ manually provides a solid foundation for interpreting this important risk metric and the term “return deviation” used to rank results. Keep in mind that this example is a simplification, and real-world return data may require more sophisticated analysis. By mastering this simple calculation, investors can gain a better understanding of the risks associated with their investments and make more informed decisions.
Delving Deeper: Population versus Sample Deviation
In statistical analysis, the ‘standard deviation of a return’ is a vital measure, but it’s crucial to understand whether to calculate the population or the sample standard deviation. The population ‘standard deviation of a return’ considers every possible data point, while the sample ‘standard deviation of a return’ only considers a subset of the population. Knowing when to use each ensures accurate risk assessment.
The population ‘standard deviation of a return’ is appropriate when you have data for the entire population of returns you are interested in. For example, if analyzing the daily returns of a stock over its entire trading history, the population standard deviation can be calculated. The formula for the population standard deviation is: σ = √[ Σ (xi – μ)² / N ], where σ is the population standard deviation, xi represents each individual return, μ is the population mean return, and N is the total number of returns in the population. This measure provides a comprehensive view of the ‘standard deviation of a return’ when all data is available.
Conversely, the sample ‘standard deviation of a return’ is used when you only have a sample of returns from the larger population. This is more common in real-world investment analysis, where you might analyze a sample of monthly returns from a mutual fund. The formula for the sample ‘standard deviation of a return’ is: s = √[ Σ (xi – x̄)² / (n-1) ], where s is the sample ‘standard deviation of a return’, xi represents each individual return in the sample, x̄ is the sample mean return, and n is the number of returns in the sample. The (n-1) term, known as Bessel’s correction, provides an unbiased estimate of the population variance. Using the sample standard deviation offers an accurate insight into the ‘standard deviation of a return’ when working with limited data, making it a practical tool for investors and analysts.
The Relationship Between Volatility and Investment Choices
The standard deviation of a return plays a pivotal role in shaping investment decisions. It acts as a quantifiable measure of risk, allowing investors to understand the potential fluctuations in their investment’s value. Risk tolerance, an investor’s capacity to withstand losses, directly correlates with their comfort level regarding the standard deviation of a return. An investor with low risk tolerance typically prefers investments with a lower standard deviation of a return, signifying less volatility and more predictable returns, even if those returns are potentially lower. Conversely, investors with a high risk tolerance might be drawn to investments exhibiting a higher standard deviation of a return, attracted by the prospect of substantial gains, while acknowledging the inherent risk of significant losses. This directly impacts what choices are made with capital, as well as when.
Consider two investment scenarios. In the first, an investor is nearing retirement and seeks to preserve their capital. They would likely favor investments like government bonds or dividend-paying stocks with a historically low standard deviation of a return. These investments offer stability and consistent income, aligning with their risk-averse profile. In the second scenario, a younger investor with a longer time horizon might allocate a portion of their portfolio to growth stocks or emerging market funds, asset classes known for their higher potential returns but also their greater standard deviation of a return. This strategic allocation reflects their willingness to accept greater volatility for the opportunity to achieve higher long-term growth. The standard deviation of a return, therefore, serves as a crucial benchmark for aligning investment choices with individual risk profiles and financial goals. Understanding how a standard deviation of a return is calculated, and how it changes based on market volatility, allows investors to make educated choices.
Furthermore, the standard deviation of a return isn’t just a theoretical number; it has real-world implications. A high standard deviation of a return can lead to emotional investing, where investors panic and sell during market downturns, locking in losses. Conversely, a low standard deviation of a return can instill a false sense of security, leading to overconfidence and potentially risky investment decisions. Therefore, a comprehensive understanding of the standard deviation of a return is paramount for making rational, informed investment decisions that are aligned with one’s risk tolerance and financial objectives. In summary, the standard deviation of a return is not an abstract concept but a critical tool for navigating the complexities of the investment landscape. By carefully considering the standard deviation of a return of different investments, investors can construct portfolios that appropriately balance risk and reward, maximizing their chances of achieving their long-term financial goals, and avoiding decisions based on emotion.
Beyond Excel: Leveraging Financial Software for Analysis
While manual calculation of the ‘standard deviation of a return’ offers a foundational understanding, modern financial analysis increasingly relies on specialized software. These tools provide efficient and sophisticated methods for handling large datasets and complex calculations. Bloomberg Terminal, a widely used platform in the financial industry, offers built-in functions to calculate and analyze the ‘standard deviation of a return’ for various assets and portfolios. It also provides access to historical data, allowing for in-depth volatility analysis over different time periods. The key is not to learn the tools but to understand how they can help us calculate sophisticated analytics.
For those seeking a more customizable and programming-oriented approach, Python libraries such as NumPy and SciPy are invaluable. NumPy provides powerful array manipulation capabilities, enabling efficient data storage and processing. SciPy, building upon NumPy, offers a comprehensive suite of statistical functions, including those for calculating the ‘standard deviation of a return.’ These libraries allow users to automate calculations, perform simulations, and develop custom analytical models. The advantage of using Python lies in its flexibility and the ability to integrate it with other data sources and analytical tools, but it requires a higher degree of technical expertise.
Financial software plays a crucial role in advanced volatility analysis by providing tools to handle vast amounts of data and perform complex calculations related to the ‘standard deviation of a return.’ These platforms enhance the efficiency and accuracy of risk assessment, enabling more informed investment decisions. They make calculating the ‘standard deviation of a return’ across various assets and time frames manageable. Remember the core concept of what the ‘standard deviation of a return’ represents remains paramount, regardless of the tool used for its calculation. Software accelerates the process and allows for greater depth of analysis, ultimately helping in the proper understanding of investment risks.
Interpreting Deviation: What Does the Number Actually Mean?
The ‘standard deviation of a return’ is not just a number; it is a powerful tool for understanding potential investment outcomes. It quantifies the dispersion of returns around the average return. A higher ‘standard deviation of a return’ indicates greater volatility, meaning returns are likely to fluctuate more dramatically. Conversely, a lower ‘standard deviation of a return’ suggests more stable and predictable returns.
To interpret the ‘standard deviation of a return,’ consider it in the context of the specific investment, the time period analyzed, and relevant benchmarks. For instance, a ‘standard deviation of a return’ of 10% for a stock indicates that, roughly speaking, about 68% of the annual returns are likely to fall within a range of plus or minus 10% of the average return. If the average return is 12%, you might anticipate returns between 2% and 22% in a given year. A ‘standard deviation of a return’ of 5% for a bond fund, however, would signal a much narrower and potentially less risky range of expected returns. Benchmarking is critical. Comparing a stock’s ‘standard deviation of a return’ to that of its market index or peers provides valuable insight into its relative riskiness.
It’s important to recognize the limitations of relying solely on ‘standard deviation of a return.’ While it effectively captures the magnitude of potential ups and downs, it does not reveal the direction or frequency of these movements. A high ‘standard deviation of a return’ could result from large positive swings, large negative swings, or a combination of both. Furthermore, ‘standard deviation of a return’ assumes a normal distribution of returns, which may not always hold true in real-world scenarios. For example, it doesn’t account for skewness, where returns are disproportionately skewed to the upside or downside. Investors should supplement their understanding of ‘standard deviation of a return’ with other risk measures and qualitative assessments to gain a more complete picture of an investment’s risk profile. The ‘standard deviation of a return’ should be used as one component of a broader due diligence process.
Risk-Adjusted Performance: Combining Deviation with Return
Evaluating investment performance requires considering both returns and the risk undertaken to achieve those returns. A crucial concept in this realm is risk-adjusted return, which incorporates the ‘standard deviation of a return’ to provide a more comprehensive assessment. While a high return might seem appealing, it is essential to understand the volatility associated with it. The ‘standard deviation of a return’ serves as a key metric for quantifying this volatility, indicating the degree to which returns have deviated from their average over a specific period.
One widely used risk-adjusted return metric is the Sharpe Ratio. This ratio calculates the excess return earned per unit of total risk. Excess return is defined as the investment’s return minus the risk-free rate (e.g., the return on a U.S. Treasury bond). The total risk is represented by the ‘standard deviation of a return.’ A higher Sharpe Ratio indicates a better risk-adjusted performance, suggesting that the investment has generated a greater return for the level of risk assumed. For example, two investments might have similar returns, but if one has a significantly lower ‘standard deviation of a return,’ its Sharpe Ratio would be higher, making it a more attractive option for risk-averse investors.
It is critical to recognize that higher returns do not automatically equate to better investments. An investment with exceptionally high returns but also a high ‘standard deviation of a return’ might be unsuitable for investors with a low-risk tolerance. Such an investment might experience significant drawdowns, potentially leading to losses that outweigh the gains. Conversely, an investment with moderate returns and a low ‘standard deviation of a return’ might be more appropriate for conservative investors seeking stable growth. By considering risk-adjusted return metrics like the Sharpe Ratio, investors can make more informed decisions, aligning their investment choices with their individual risk profiles and financial goals. The ‘standard deviation of a return’ is therefore not just a measure of volatility, but a vital component in evaluating overall investment performance and suitability.
Strategies to Mitigate Volatility in Investment Portfolio
Managing portfolio risk is crucial for investors seeking to protect their capital and achieve long-term financial goals. Several strategies exist to mitigate volatility and reduce the potential impact of market fluctuations. A well-diversified portfolio is a cornerstone of risk management. By spreading investments across various asset classes, such as stocks, bonds, and real estate, investors can reduce the impact of any single investment’s performance on the overall portfolio. The principle behind diversification is that different asset classes react differently to market conditions. When one asset class declines, others may remain stable or even increase in value, offsetting the losses. This diversification helps to smooth out returns and lower the overall ‘standard deviation of a return’ of the portfolio.
Asset allocation is another key strategy for managing portfolio volatility. This involves determining the appropriate mix of assets based on an investor’s risk tolerance, time horizon, and financial goals. A conservative investor with a short time horizon may allocate a larger portion of their portfolio to lower-risk assets like bonds, while a more aggressive investor with a longer time horizon might allocate a greater percentage to stocks. Rebalancing the portfolio periodically is essential to maintain the desired asset allocation. Over time, some asset classes may outperform others, causing the portfolio’s allocation to drift away from its original target. Rebalancing involves selling some of the overperforming assets and buying underperforming ones to restore the original allocation. This process helps to ensure that the portfolio remains aligned with the investor’s risk tolerance and reduces the risk of overexposure to any single asset class. The ‘standard deviation of a return’ should be monitored alongside returns during rebalancing to ensure risk levels remain appropriate.
Hedging instruments can also be employed to mitigate volatility in investment portfolios. Hedging involves taking offsetting positions in related assets to protect against potential losses. For example, an investor holding a stock portfolio might purchase put options on a stock index to protect against a market downturn. If the market declines, the value of the put options will increase, offsetting some of the losses in the stock portfolio. Another hedging strategy involves using inverse exchange-traded funds (ETFs), which are designed to move in the opposite direction of a specific index or asset class. While hedging can help to reduce portfolio volatility, it also involves costs, such as the premiums paid for options or the management fees charged by inverse ETFs. Investors should carefully weigh the costs and benefits of hedging before implementing such strategies. Regardless of the specific strategies employed, it is crucial to regularly monitor portfolio performance and adjust the risk management approach as needed. The ‘standard deviation of a return’ serves as a critical metric in assessing the effectiveness of these strategies and ensuring that the portfolio remains aligned with the investor’s risk tolerance and financial goals.