Understanding Data Distribution: Left Skewed vs Right Skewed
Data distribution forms the bedrock of statistical analysis, providing insights into the underlying patterns of data sets. Skewness, a critical measure within data distribution, quantifies the asymmetry present in a probability distribution. It reveals the degree to which data points cluster more on one side of the distribution than the other. A distribution is considered skewed when it is not symmetrical. Skewness is a fundamental concept for anyone working with data. Understanding skewness ensures accurate data interpretation and informed decision-making. Recognizing whether a dataset is positively skewed vs negatively skewed allows for the application of appropriate statistical techniques. This is particularly crucial when comparing positively skewed vs negatively skewed distributions.
The shape of a data distribution significantly impacts the conclusions drawn from statistical analyses. Skewness indicates the direction and magnitude of the asymmetry. This measure helps to differentiate between positively skewed vs negatively skewed datasets. A symmetrical distribution, such as a normal distribution, has zero skewness. However, many real-world datasets exhibit skewness, highlighting the importance of understanding this concept. By identifying skewness, analysts can select the most appropriate statistical methods. These methods provide accurate representations and insights into the data.
This discussion will delve into the characteristics of positively skewed vs negatively skewed distributions. It will also explore the implications of skewness for statistical measures like mean, median and mode. The goal is to equip readers with the ability to identify and interpret skewness in various contexts. Understanding the nuances of positively skewed vs negatively skewed distributions is vital for drawing valid conclusions and making sound judgments based on data analysis. Recognizing and addressing skewness leads to a deeper understanding of the data.
Delving into Positively Skewed Distributions (Right Skewed)
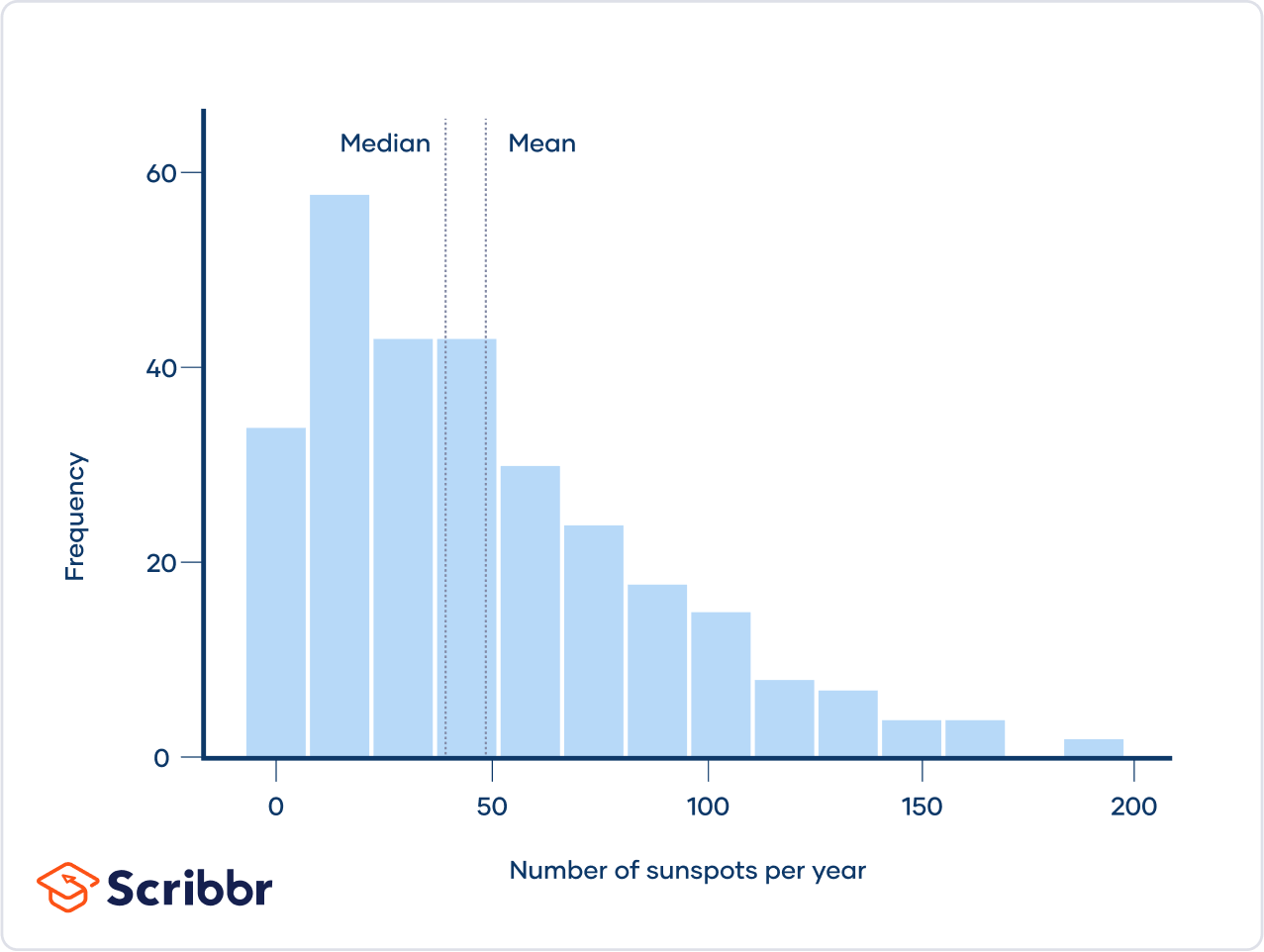
A positively skewed distribution, also known as a right-skewed distribution, is a type of data distribution where the tail extends more towards the right side of the graph. This means that the majority of the data points are concentrated on the left, with fewer data points trailing off to the right. In a positively skewed distribution, the mean is typically greater than the median because the extreme values on the right side pull the mean upwards. Understanding the concept of positively skewed vs negatively skewed distributions is essential for accurate data interpretation.
Real-world examples of data sets that often exhibit positive skewness include income distribution, housing prices in certain areas, and website session durations. For example, when analyzing income distribution, most people earn a moderate income, while a smaller number of individuals earn significantly higher incomes, creating a long tail to the right. Similarly, when examining housing prices in a specific area, many homes may fall within a certain price range, but a few luxury properties can significantly increase the average price, resulting in a positively skewed distribution. Website session durations also often show positive skewness. Many users might spend only a few minutes browsing, but some dedicated users might stay on the site for hours, creating a long tail on the right. This difference between positively skewed vs negatively skewed data is crucial for businesses to understand user engagement.
Consider the example of website session times. Most users might spend a short time browsing, but a few dedicated users might stay for hours. This creates a long tail to the right and a positively skewed distribution. Identifying a positively skewed vs negatively skewed distribution helps in choosing appropriate statistical measures. In such cases, the median might be a more representative measure of central tendency than the mean, as the mean is more susceptible to the influence of outliers. Recognizing the characteristics of a positively skewed distribution is vital for making informed decisions based on data analysis.
Exploring Negatively Skewed Distributions (Left Skewed)
A negatively skewed distribution, also known as left-skewed, occurs when the tail on the left side of the distribution is longer or fatter than the tail on the right side. In this type of distribution, the majority of the data points are concentrated on the higher end of the scale, resulting in a longer tail extending towards the lower values. This contrasts with positively skewed vs negatively skewed distributions, where the tail extends towards higher values. Consequently, the mean is typically less than the median in a negatively skewed distribution.
Real-world examples of data sets that often exhibit negative skewness include exam scores where most students perform well. The distribution will be skewed to the left because the tail will extend more towards the lower scores. Another example could be the age of retirement in a population with provisions for early retirement, where a significant number of individuals retire earlier, creating a tail towards the younger ages. Understanding positively skewed vs negatively skewed distributions is critical for accurate data interpretation.
Consider test scores where the majority of students achieve high grades. The distribution will be skewed to the left because the tail will extend more towards the lower scores. In such scenarios, focusing solely on the mean might be misleading as it is pulled down by the few lower scores, not accurately reflecting the typical performance. Therefore, when comparing positively skewed vs negatively skewed data, it’s important to select appropriate statistical measures and visualizations that account for the asymmetry in the data.
Visual Aids: Charts and Graphs to Identify Skewness
The visual representation of data is crucial for understanding its distribution, especially when dealing with skewness. Histograms and box plots are particularly useful tools for identifying whether a dataset is positively skewed vs negatively skewed. These visual aids allow for a quick assessment of the data’s symmetry and the direction of any existing skew. Analyzing these plots is key to differentiate positively skewed vs negatively skewed data.
Histograms display the frequency distribution of data. In a positively skewed distribution, also known as right-skewed, the histogram will show a longer tail extending to the right. The bulk of the data, including the peak, will be concentrated on the left side. Conversely, in a negatively skewed distribution, or left-skewed distribution, the histogram will have a longer tail extending to the left, with the peak of the data concentrated on the right side. When interpreting histograms, focus on the tail’s direction to determine if the distribution leans towards positively skewed vs negatively skewed. Understanding positively skewed vs negatively skewed distributions is a fundamental skill in data analysis.
Box plots offer another perspective on data skewness. A box plot displays the median, quartiles, and potential outliers of a dataset. In a positively skewed dataset, the median will be closer to the lower quartile, and the whisker on the right side will be noticeably longer than the whisker on the left. This visual asymmetry indicates a right-skewed distribution. In a negatively skewed dataset, the median will be closer to the upper quartile, and the left whisker will be longer than the right whisker, signaling a left-skewed distribution. By examining the relative lengths of the whiskers and the median’s position within the box, one can effectively discern between positively skewed vs negatively skewed data. Recognizing positively skewed vs negatively skewed characteristics in data visualization enhances analytical accuracy.
The Impact of Skewness on Statistical Measures: Mean, Median, and Mode
Skewness significantly affects the relationship between the mean, median, and mode in a dataset. Understanding these effects is crucial for accurate data interpretation. In a positively skewed distribution, also known as right-skewed, the mean is typically greater than the median, which is greater than the mode. This occurs because the long tail on the right side pulls the mean towards higher values. The mean, being the average of all data points, is more sensitive to extreme values or outliers than the median, which represents the middle value. Therefore, in a positively skewed vs negatively skewed distribution, the mean is a less robust measure of central tendency.
Conversely, in a negatively skewed distribution, also known as left-skewed, the mean is typically less than the median, which is less than the mode. In this scenario, the long tail on the left side pulls the mean towards lower values. Again, the mean’s sensitivity to outliers is the driving force behind this difference. The median remains a more stable measure of central tendency, as it is not as affected by extreme values. The mode, representing the most frequent value, is also influenced by the shape of the distribution. When dealing with positively skewed vs negatively skewed data, selecting the appropriate measure of central tendency depends on the specific context and the goals of the analysis. If minimizing the impact of outliers is important, the median is often preferred.
Choosing the correct measure of central tendency is important depending on the skew of the data. For example, consider income data, which is often positively skewed. Using the mean income might give a misleading impression of the “typical” income, as it can be inflated by a few very high earners. In such cases, the median income would be a more representative measure. Understanding the interplay between skewness and these statistical measures allows for more informed decision-making and accurate data interpretation. Recognizing whether data is positively skewed vs negatively skewed is a fundamental step in any statistical analysis, guiding the selection of appropriate analytical techniques and ensuring meaningful conclusions.
Skewed Distributions: Common Misconceptions and Pitfalls
A common misconception is that all data should conform to a normal distribution. In reality, many datasets exhibit skewness, reflecting the inherent nature of the variable being measured. Assuming normality when it doesn’t exist can lead to inaccurate statistical inferences. Applying statistical methods designed for normally distributed data to skewed data without appropriate adjustments is a potential pitfall. For example, using a t-test on highly skewed data might produce unreliable p-values. Understanding data distribution is crucial before making inferences or drawing conclusions from statistical analysis. Failing to account for skewness can result in biased estimates and flawed interpretations. It’s essential to choose statistical tests and models that are appropriate for the underlying distribution of the data. The terms positively skewed vs negatively skewed are fundamental in understanding data analysis.
Another misconception is that skewness always indicates a problem with the data. Skewness can simply reflect the true distribution of the variable. For instance, income data is often positively skewed, with a few individuals earning significantly more than the majority. This skewness is not necessarily an error but a characteristic of income distribution. Similarly, the age of retirement might be negatively skewed if a significant portion of people retire around the same age. Recognizing when skewness is a natural feature of the data is vital for proper interpretation. Data transformations can be applied to reduce skewness, but it’s essential to consider whether the transformation is appropriate and justifiable in the context of the analysis. The differences between positively skewed vs negatively skewed distributions are important to consider.
It’s important to avoid overlooking the impact of outliers on skewness. Outliers can significantly influence the shape of a distribution, potentially exaggerating or masking the underlying skew. Robust statistical methods, which are less sensitive to outliers, can be valuable for analyzing skewed data. Moreover, visualizations such as box plots and histograms can help identify outliers and assess their impact on the distribution. Always explore the data thoroughly before drawing conclusions about skewness. Remember that positively skewed vs negatively skewed data require different approaches.
Transforming Skewed Data: Techniques and Tools
Data transformation techniques offer solutions to mitigate the effects of skewness, enhancing data symmetry and improving the reliability of statistical analyses. When data deviates significantly from a normal distribution, transformations can reshape the data, making it more suitable for certain statistical methods. Several techniques are available, each designed to address specific types of skewness. Logarithmic transformations are effective for reducing positive skewness, compressing the right tail of the distribution. This method involves applying a logarithmic function to each data point, which can stabilize variance and normalize the data. Square root transformations are another option for addressing positive skewness, providing a milder effect than logarithmic transformations. This involves taking the square root of each data point. When dealing with more complex skewness patterns, the Box-Cox transformation is a powerful tool. This is a family of transformations that includes logarithmic and power transformations, allowing for a flexible approach to normalizing data. The Box-Cox transformation requires estimating a parameter that determines the optimal transformation for a given dataset.
Specialized software and libraries, such as those in R and Python, offer functions to facilitate these transformations. For example, in Python, the NumPy and SciPy libraries provide functions for logarithmic, square root, and Box-Cox transformations. In R, functions like log(), sqrt(), and boxcox() from the “MASS” package are commonly used. These tools automate the transformation process, making it easier to apply these techniques to large datasets. Understanding when *not* to transform data is equally important. In some cases, skewness is inherent to the nature of the variable being measured and carries meaningful information. For instance, in income data, the *positively skewed vs negatively skewed* distribution reflects real-world economic disparities. Transforming such data might obscure these important insights. The decision to transform data should be based on a careful consideration of the statistical goals and the interpretability of the results. Applying transformations without understanding the underlying data can lead to misleading conclusions. Therefore, it is crucial to assess the impact of transformations on the data and ensure that the transformed data still accurately represents the phenomenon under investigation. For example, consider a *positively skewed vs negatively skewed* distribution related to customer satisfaction scores; transforming this data might distort the true sentiment distribution.
The goal of these transformations is to achieve a more normal distribution, enabling the application of statistical methods that assume normality. However, it is essential to validate the effectiveness of the transformation by examining the distribution of the transformed data. Visual aids, such as histograms and Q-Q plots, can help assess whether the transformation has successfully reduced skewness. Furthermore, statistical tests for normality, like the Shapiro-Wilk test, can provide a quantitative assessment of the transformation’s impact. Remember, the appropriateness of a *positively skewed vs negatively skewed* data transformation depends on the specific context and the goals of the analysis.
Practical Applications: Interpreting Skewness in Real-World Scenarios
Context_8: Understanding skewness is vital in various real-world scenarios. In finance, analyzing stock returns often reveals positively skewed vs negatively skewed distributions. A positively skewed distribution might indicate infrequent but significant gains, while a negatively skewed distribution could suggest consistent smaller gains with rare large losses. Considering skewness helps investors understand potential risks and rewards beyond average returns. Similarly, in healthcare, analyzing patient outcomes, such as length of hospital stay, can exhibit skewness. A positively skewed distribution might indicate that most patients have short stays, but a few require prolonged care, impacting resource allocation and hospital management. In marketing, analyzing customer demographics, like income levels or purchase frequency, often reveals skewed patterns. Income data is frequently positively skewed vs negatively skewed, with a long tail of high earners. Understanding this skewness is crucial for targeted advertising and product development.
Skewness significantly impacts decision-making across different fields. In finance, failing to account for positively skewed vs negatively skewed returns can lead to underestimating potential losses. In healthcare, overlooking skewness in patient data can result in inadequate resource planning. In marketing, ignoring income skewness may result in ineffective marketing campaigns. Therefore, considering skewness when interpreting data is paramount for making informed decisions based on statistical analysis. Analyzing customer feedback scores, often collected through surveys, may show negative skewness if most customers are satisfied. However, identifying the reasons behind the lower scores in the left tail is crucial for improving customer service and product quality.
The key differences between positively skewed vs negatively skewed distributions lie in the direction of their tails and the relationship between the mean, median, and mode. A positively skewed distribution has a longer tail on the right, with the mean typically greater than the median. Conversely, a negatively skewed distribution has a longer tail on the left, with the mean typically less than the median. Accurate identification and interpretation of skewness are essential for drawing valid conclusions from data. For example, if a company reports average sales figures without acknowledging a positively skewed sales distribution, it might mislead investors about the typical sales performance. Understanding the nuances of positively skewed vs negatively skewed data ensures more reliable and insightful analysis, leading to better-informed decisions.