Understanding Stock Relationships and Why Covariance Matters
Stock prices often move in relation to each other. Understanding these relationships is crucial for effective portfolio diversification and risk management. One key tool for analyzing this relationship is covariance. Covariance measures the directional relationship between two stocks. A positive covariance suggests that the stocks tend to move in the same direction. Conversely, a negative covariance indicates they tend to move in opposite directions. Learning how to calculate covariance of two stocks is essential for investors seeking to optimize their portfolios. Imagine two stocks: one consistently rises when the other rises, and vice versa. This indicates a positive covariance and a high degree of correlation. Conversely, if one stock tends to rise while the other falls, the covariance will be negative, suggesting an inverse relationship. Understanding how to calculate covariance of two stocks allows investors to quantify this relationship precisely. This is vital because the goal of diversification is to minimize overall portfolio risk by combining assets that don’t move perfectly together. Knowing how to calculate covariance of two stocks helps in achieving this goal effectively. By understanding the interplay of different stocks within a portfolio, investors can minimize potential losses during market downturns. This knowledge empowers them to make better investment decisions.
To truly grasp the concept of covariance, consider a simple example. Suppose Stock A and Stock B both increase in value on the same days and decrease on the same days. Their movements show a strong positive relationship. This positive relationship will be reflected in a high positive covariance value when you learn how to calculate covariance of two stocks. Conversely, if Stock A rises when Stock B falls and vice versa, indicating an inverse relationship, the covariance will be negative. The magnitude of the covariance reflects the strength of this relationship; a larger magnitude (either positive or negative) represents a stronger relationship. This is why learning how to calculate covariance of two stocks is so important. By understanding the covariance between assets, investors can design portfolios that are more resilient to market fluctuations. The ability to calculate covariance enables informed decisions about asset allocation, thereby leading to a more robust and stable investment strategy. It’s a vital tool in any investor’s toolkit.
The process of how to calculate covariance of two stocks involves several steps. First, one needs to gather historical stock price data. This data forms the foundation for all subsequent calculations. Accurate data is crucial; using unreliable data will result in inaccurate conclusions about the relationship between the two stocks. Learning how to calculate covariance of two stocks involves using this data to calculate daily returns and then using those returns to perform the covariance calculation. Understanding the significance of covariance and its role in portfolio management is paramount. A thorough understanding of the techniques used in calculating covariance, including the proper use of returns and the correct interpretation of the results, is necessary for making sound investment decisions. Learning how to calculate covariance of two stocks is a valuable skill for any serious investor.
Gathering the Necessary Data: Stock Price History
To calculate the covariance of two stocks, one must first obtain historical stock price data. Reliable sources for this data include Yahoo Finance, Google Finance, and various financial APIs. These platforms provide extensive historical data, often going back many years. When choosing a data source, ensure the data’s accuracy and reliability. Selecting a consistent timeframe for analysis is crucial for meaningful results. Inconsistent timeframes can introduce biases and inaccuracies into the covariance calculation. For example, using data from only bull markets will skew the results differently than data from both bull and bear markets. Daily closing prices are generally preferred for covariance calculations, as they provide a consistent and readily available snapshot of the market’s daily performance. This approach avoids the complications of intraday price fluctuations, simplifying the calculation of returns and enhancing the reliability of covariance calculations. The selection of an appropriate timeframe and data frequency significantly impacts the accuracy and interpretation of the covariance calculation. Consider using an appropriate time horizon, such as one year or five years, to reflect the desired investment horizon. This choice influences the representation of the relationship between the two stocks.
Accessing historical stock price data is straightforward using these online resources. Many offer free access to basic data, making it easy for individual investors to begin their analysis of stock correlation. More advanced features, such as access to more granular data or real-time feeds, are often available through paid subscriptions or APIs. Regardless of the chosen source, carefully review the data for any inconsistencies or errors before proceeding with covariance calculations. This preliminary step helps to ensure data integrity and improve the reliability of subsequent calculations. For example, data gaps or unexpected jumps in price can indicate errors that need correction before proceeding. When working with APIs, remember to adhere to any usage limits or terms of service provided by the API provider to avoid potential issues.
Understanding how to obtain and prepare this data is fundamental to calculating the covariance of two stocks. The quality of the input data directly affects the accuracy and meaningfulness of the final covariance result. Therefore, careful attention should be given to data source selection, timeframe consistency, and data cleaning to achieve reliable results when calculating covariance. Remember that accurate data is essential for any meaningful financial analysis; the need for thorough data preparation cannot be overstated when attempting to measure the relationships between stock prices. High-quality data ensures accurate covariance calculation and supports informed investment decisions.
Calculating Returns: The Foundation of Covariance
To calculate the covariance of two stocks, one must first compute the daily percentage returns for each stock. This forms the foundation for understanding how the stocks’ prices move relative to each other. The formula for calculating daily percentage return is: (Today’s Price – Yesterday’s Price) / Yesterday’s Price. For example, if a stock’s price was $100 yesterday and $102 today, the daily percentage return is (102 – 100) / 100 = 0.02 or 2%. This simple calculation is repeated for each day in the historical dataset. Using percentage returns, rather than absolute price changes, allows for a standardized comparison across stocks with different price levels. This is crucial when learning how to calculate covariance of two stocks.
It’s important to consistently apply this calculation to both stock datasets across the chosen timeframe. This consistency ensures accuracy in subsequent steps of the covariance calculation. For instance, if analyzing data from January 1st to March 31st, the same period must be used for both stocks. Daily closing prices are typically preferred for this calculation, as they represent the final price for the trading day and provide a clean data point for analysis. While daily percentage returns are sufficient for many calculations, using logarithmic returns can offer advantages in certain situations. Logarithmic returns are particularly useful when dealing with larger price swings or when accuracy is paramount in the calculation of covariance of two stocks. They provide a more symmetrical distribution and avoid potential issues with compounding. This method involves taking the natural logarithm of the ratio of consecutive prices: ln(Today’s Price / Yesterday’s Price). The choice of method depends on the specific needs of the analysis and the nature of the stock price data.
The consistent application of this return calculation, whether using simple percentage changes or logarithmic returns, is crucial. It directly impacts the accuracy of the subsequent steps, leading to a reliable covariance value. Understanding how to accurately calculate daily returns is a foundational step in learning how to calculate covariance of two stocks and interpreting the resulting relationships between the assets. The quality of the covariance calculation depends heavily on the accuracy of the initial return calculations. Remember, these are intermediate steps in determining the covariance of two stocks, essential in understanding financial market dynamics and optimizing investment strategies. Precise calculation is fundamental for accurate conclusions about the relationship between the two stocks.
Calculating the Average Returns: Centering the Data
To calculate the covariance of two stocks, one must first determine the average daily return for each stock. This crucial step centers the data, preparing it for the covariance calculation. The average daily return represents the typical daily percentage change in the stock’s price over the selected period. To calculate this average, sum all the daily percentage returns for a given stock and divide by the total number of days. For example, if you have calculated daily returns for 100 days, you will sum those 100 returns and then divide the sum by 100. This provides the mean, or average daily return for that stock. Repeat this process for the second stock. Accurate averaging is essential to avoid bias in the subsequent covariance calculation; any errors here will propagate through the entire process. Remember, this average return calculation is a fundamental part of learning how to calculate covariance of two stocks.
Consider a hypothetical example. Suppose Stock A has daily returns of 1%, 2%, -0.5%, and 1.5% over four days. The sum of these returns is 4%. Dividing this sum by four (the number of days) gives an average daily return of 1% for Stock A. Similarly, calculate the average daily return for Stock B using the same method. The accuracy of these average daily return calculations is paramount to the accuracy of the final covariance calculation and to correctly understanding how to calculate covariance of two stocks.
This step of calculating average daily returns is vital in the process of determining how to calculate covariance of two stocks. It involves summing all the daily percentage returns for each stock, then dividing by the total number of days. This process provides the average daily return for each stock. These averages are used to center the data and allow for accurate determination of each individual data point’s deviation from the mean. The precise calculation of these average daily returns forms the foundation for calculating covariance, so care must be taken to ensure accuracy and eliminate any sources of bias. Understanding how to calculate covariance of two stocks involves mastering this average calculation and recognizing its importance in the overall process.
Calculating the Deviations from the Mean: Measuring Dispersion
To calculate the covariance of two stocks, understanding how each stock’s daily return deviates from its average is crucial. This involves calculating the difference between each daily return and the average daily return for that stock. This process centers the data around zero, making the covariance calculation more meaningful. The formula for calculating the deviation is straightforward: Deviation = Daily Return – Average Daily Return. For example, if a stock’s average daily return is 0.5% and a specific day’s return is 1%, the deviation is 1% – 0.5% = 0.5%. Note that deviations can be positive or negative, indicating whether the daily return was above or below the average. Positive deviations show returns exceeding the average, while negative deviations represent returns falling below the average. This step is essential for determining how much each daily return varies from its average, a key factor in understanding the relationship between two stocks. Analyzing these deviations for both stocks prepares the data for the subsequent covariance calculation, a critical step in learning how to calculate covariance of two stocks.
Calculating these deviations for each stock is a crucial preprocessing step before calculating the covariance. It helps to standardize the data, facilitating a more accurate and reliable measure of the relationship between the two stocks’ returns. The significance of positive and negative deviations lies in their contribution to the overall covariance calculation. A large positive deviation in one stock paired with a large positive deviation in another suggests a positive relationship. Conversely, a large positive deviation in one stock paired with a large negative deviation in the other indicates a negative relationship. These relationships are quantified in the final covariance calculation. Remember to maintain accuracy in calculating both the average daily returns and the individual deviations. This precision is essential for a reliable covariance calculation, crucial in understanding how to calculate covariance of two stocks effectively.
The process of calculating deviations from the mean for each stock’s daily returns is fundamental to understanding how to calculate covariance of two stocks. Each deviation represents the distance of a specific daily return from the average return. Analyzing the distribution of these deviations provides insights into the volatility and variability of each stock’s returns. These deviations are then used in the covariance calculation, which ultimately reveals the directional relationship between the two stocks. Accurate calculation of these deviations is paramount for obtaining a precise and reliable measure of the covariance. Understanding these deviations is a necessary prerequisite for mastering the calculation of covariance and interpreting the resulting value.
The Covariance Calculation: Putting it All Together
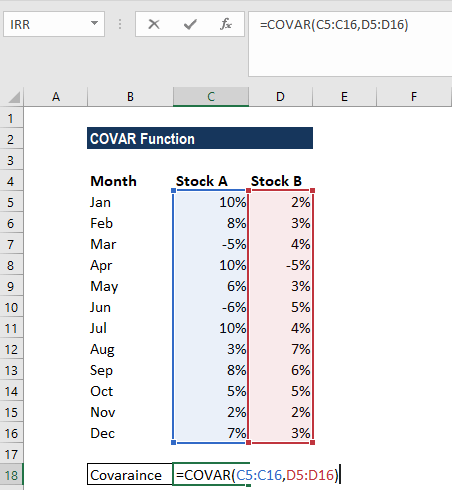
To understand how to calculate covariance of two stocks, one must first compute the daily percentage returns for each stock. Then, calculate the average daily return for each. Next, find the deviation of each daily return from its respective average. These deviations represent how much each daily return varies from its mean. Finally, the covariance is calculated using the following formula: Covariance = Σ [(ReturnStock A – Average ReturnStock A) * (ReturnStock B – Average ReturnStock B)] / (Number of Observations – 1). This formula sums the product of the deviations of each stock’s daily return from its average, then divides by the number of observations minus one. This adjustment provides an unbiased estimate of the population covariance. The result represents the covariance between the two stocks. The units are percentage squared.
Let’s illustrate how to calculate covariance of two stocks with a hypothetical example. Suppose we have daily returns for Stock A and Stock B over a 10-day period. We would calculate the average daily return for each stock. Then, for each day, we would calculate the deviation of the return from the average return for both Stock A and Stock B. We would then multiply these deviations for each day. Summing these products and dividing by 9 (10-1) would yield the covariance. A positive covariance suggests the stocks tend to move together; a negative covariance indicates they tend to move in opposite directions; and a covariance near zero suggests a weak or no linear relationship. Learning how to calculate covariance of two stocks is crucial for understanding their relationship and managing investment risk effectively. Remember that the covariance itself is difficult to interpret directly due to its scale. Therefore, understanding correlation, which standardizes covariance, is essential.
To further clarify how to calculate covariance of two stocks, consider the importance of using consistent data. Inaccurate or inconsistent data will result in an inaccurate covariance calculation. The accuracy of the covariance calculation directly depends on the quality of the input data. Therefore, the selection of reliable data sources is crucial for obtaining meaningful results. The steps involved in calculating covariance are straightforward, yet each step requires precision to ensure the accuracy of the final result. A careful and methodical approach to each step is crucial for deriving a reliable measure of the relationship between the two stocks. Mastering how to calculate covariance of two stocks enables investors to build more effective and diversified portfolios. The covariance, though valuable, provides only one aspect of the relationship. Remember to examine the correlation coefficient for a more standardized and readily interpretable measure.
Interpreting the Covariance: Understanding the Results
The calculated covariance value provides insights into the directional relationship between two stocks. A positive covariance indicates that the stocks tend to move in the same direction. When one stock’s return is above average, the other’s return is also likely above average, and vice versa. Conversely, a negative covariance suggests the stocks move in opposite directions. When one stock outperforms its average, the other tends to underperform. A covariance of zero implies no linear relationship between the stock returns; their movements are independent of each other. This understanding is crucial when learning how to calculate covariance of two stocks. Remember, a key aspect of how to calculate covariance of two stocks accurately is to ensure data accuracy and consistency. It’s important to note that interpreting covariance requires caution. The magnitude of the covariance doesn’t directly reflect the strength of the relationship. A large covariance could simply reflect high volatility in both stocks. It’s crucial to analyze covariance alongside individual standard deviations to gain a more complete understanding of the relationship.
To illustrate, consider two stocks with a high positive covariance. This suggests they tend to move together. However, if one stock is significantly more volatile than the other (as reflected in their respective standard deviations), their price movements may not be perfectly synchronized despite the high covariance. Therefore, while understanding how to calculate covariance of two stocks is fundamental, it’s vital to interpret the result in context. Focusing solely on the covariance value can be misleading. A comprehensive analysis considers the covariance in relation to the individual volatilities (standard deviations) of the assets involved. This nuanced perspective offers a richer understanding of the relationship’s strength and implications for portfolio diversification. Accurate covariance calculation, which is crucial when learning how to calculate covariance of two stocks, aids in better portfolio risk management. The next step in a comprehensive analysis is frequently to calculate and analyze correlation.
Understanding how to calculate covariance of two stocks is a valuable skill for investors. However, the covariance alone doesn’t tell the whole story. It only provides information about the direction of the relationship. To understand the strength of this relationship, one needs to look at the correlation coefficient. The correlation coefficient, ranging from -1 to +1, provides a standardized measure of the linear relationship. A value of +1 indicates a perfect positive correlation, -1 indicates a perfect negative correlation, and 0 implies no linear correlation. While learning how to calculate covariance of two stocks is essential, understanding correlation offers a more interpretable measure of the strength and direction of the relationship between the two assets. This adds another layer of sophistication to investment analysis. Using both covariance and correlation leads to a more complete understanding of the relationship between two assets than using covariance alone. This approach helps investors manage risk more effectively and make informed decisions.
Beyond Covariance: Exploring Correlation for a Standardized Measure
While covariance provides valuable insight into the directional relationship between two stocks, its interpretation can be challenging. Covariance values are not standardized; they depend on the scale of the stock price movements. A high covariance value might simply reflect high volatility in both stocks, not necessarily a strong relationship. This is where correlation comes in. Correlation offers a standardized measure of the linear relationship, resolving the scale dependency issue. To understand how to calculate covariance of two stocks fully, one must grasp correlation’s role in providing a clearer picture.
Correlation is calculated by dividing the covariance of two stocks by the product of their individual standard deviations. This normalization process produces a value that always falls between -1 and +1. A correlation of +1 indicates a perfect positive linear relationship: when one stock rises, the other rises proportionally. A correlation of -1 signifies a perfect negative linear relationship: when one stock rises, the other falls proportionally. A correlation of 0 suggests no linear relationship between the two stock price movements. The calculation of correlation helps in interpreting the relationship between stocks more easily than just considering the covariance. Understanding how to calculate covariance of two stocks involves also understanding the use of the correlation coefficient.
Therefore, while learning how to calculate covariance of two stocks is fundamental, it’s crucial to interpret the results in conjunction with correlation. Correlation provides a more intuitive and easily comparable measure of the strength and direction of the linear relationship between the two assets. This standardized metric allows for better comparisons across different pairs of stocks, offering a clearer perspective on portfolio diversification strategies and risk assessment when compared to covariance alone. Considering both covariance and correlation together provides a comprehensive understanding of the relationship between stock prices. The calculation of correlation provides a more readily interpretable measure of the relationship between the two stocks than covariance alone.