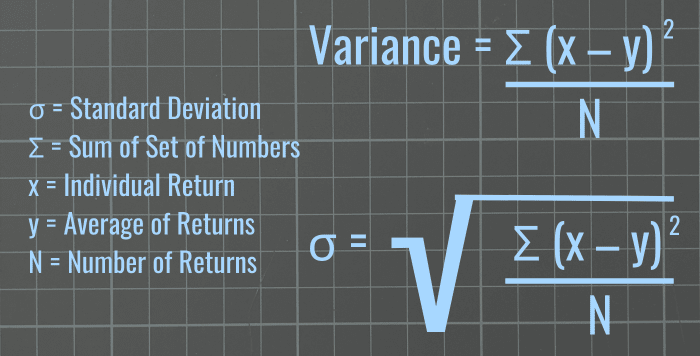Understanding Investment Returns and Their Variability
Investing involves putting your money into assets with the expectation of generating a profit. Investment returns represent the profit or loss you experience. These returns aren’t fixed; they fluctuate. Understanding this variability is essential for making sound financial decisions. Risk, in the investment world, is directly tied to how much these returns change. High variability means high risk, while low variability suggests lower risk. This section lays the groundwork for understanding standard deviation of the returns as a key tool for measuring this variability.
Returns can vary dramatically depending on the investment. Some investments offer steady, predictable returns, while others experience significant ups and downs. This fluctuation, often referred to as volatility, directly impacts your investment strategy. For example, a conservative investor might prioritize stability and choose investments with low volatility. In contrast, an aggressive investor might accept higher volatility to potentially achieve greater returns. Accurately measuring this volatility is critical, and the standard deviation of the returns offers a powerful method for doing so. Successfully navigating the investment landscape requires a firm grasp of risk and return, and the standard deviation of the returns is an important metric in that process.
To effectively manage risk and make informed decisions, investors need reliable metrics. The standard deviation of the returns provides a quantifiable measure of investment volatility. A higher standard deviation indicates greater uncertainty and risk, meaning returns are more likely to deviate significantly from the average. Conversely, a lower standard deviation suggests more stable returns, with less extreme variation around the average. Mastering the concept of the standard deviation of the returns will enhance your understanding of investment risk, enabling more strategic and confident decision-making. This understanding is particularly crucial when comparing different investment options and constructing a well-diversified portfolio. The standard deviation of the returns is not just a statistical concept; it’s a practical tool for managing your financial future.
What is Standard Deviation in the Context of Investment Returns?
Standard deviation measures the variability or dispersion of a set of investment returns around their average. Imagine a scatter plot showing investment returns over time. The standard deviation quantifies how spread out those data points are. A larger spread indicates higher volatility, meaning returns fluctuate more significantly. Conversely, a smaller spread suggests more stable, predictable returns. Understanding the standard deviation of the returns is vital for assessing investment risk. A high standard deviation of the returns signifies greater risk, as returns are more likely to deviate substantially from the average. Conversely, a low standard deviation of the returns suggests lower risk and more consistent performance.
Think of it like this: two investments might have the same average return, but one could have a much higher standard deviation. This means the high standard deviation investment will experience more extreme gains and losses compared to the investment with a lower standard deviation. While both may offer the same average return over the long term, the experience will be vastly different. The standard deviation of the returns provides crucial insight into the potential for larger swings in your investment’s value. This is a key factor in determining how suitable an investment is for your risk tolerance.
In simpler terms, the standard deviation of the returns is a statistical measure that helps investors quantify the risk associated with an investment. A higher standard deviation indicates greater volatility and higher potential risk. A lower standard deviation suggests more stable returns and lower risk. Investors use this measure to compare the risk profiles of different investments and make informed decisions aligned with their risk tolerance and investment objectives. The standard deviation of the returns is a critical tool for understanding and managing investment risk effectively. It allows for a more precise assessment of potential fluctuations and helps tailor investment strategies to individual needs.
How to Calculate the Standard Deviation of Investment Returns
Calculating the standard deviation of the returns for an investment provides a quantifiable measure of its volatility. This calculation helps investors understand the risk associated with that particular investment. The process involves several steps. First, determine the average return. This is done by summing all individual returns and dividing by the number of returns. Next, find the difference between each individual return and the average return. Square each of these differences. This step is crucial because it eliminates negative values, ensuring all variations contribute positively to the overall measure of volatility. Then, sum all the squared differences. This sum represents the total squared deviation from the average return. Divide this sum by the number of returns minus one (this is known as the sample standard deviation, which is generally used when analyzing a sample of returns, not the entire population). Finally, take the square root of the result. This final number is the standard deviation of the returns. A higher standard deviation indicates greater volatility and, consequently, higher risk.
Let’s illustrate with a simple example. Suppose an investment has yielded the following annual returns over five years: 10%, 15%, -5%, 20%, and 8%. First, calculate the average return: (10% + 15% – 5% + 20% + 8%) / 5 = 9.6%. Next, calculate the squared differences from the average: (10% – 9.6%)² = 0.0016; (15% – 9.6%)² = 0.2916; (-5% – 9.6%)² = 2.1609; (20% – 9.6%)² = 1.0816; (8% – 9.6%)² = 0.0256. Sum these squared differences: 0.0016 + 0.2916 + 2.1609 + 1.0816 + 0.0256 = 3.5613. Divide this sum by (5-1) = 4: 3.5613 / 4 = 0.8903. Finally, take the square root: √0.8903 ≈ 0.9435 or 9.435%. This means the standard deviation of these returns is approximately 9.435%. This relatively high standard deviation suggests considerable volatility in the investment’s returns. Software like Excel or Google Sheets can easily perform this calculation, avoiding manual calculations for larger datasets.
Understanding how to calculate the standard deviation of the returns is vital for assessing investment risk. While the example uses annual returns, the same method applies to any time period. The frequency of the returns used (e.g., monthly, quarterly) will influence the interpretation of the resulting standard deviation. A higher frequency (e.g., daily returns) generally results in a higher standard deviation due to the increased potential for short-term fluctuations. Investors should remember that a high standard deviation doesn’t automatically mean an investment is bad, but it indicates higher potential volatility. The appropriate level of risk depends entirely on the investor’s risk tolerance and financial goals. Careful consideration of the standard deviation, alongside other factors, is key to making informed investment decisions. The standard deviation of the returns is a crucial tool in investment analysis, providing valuable insights into the risk associated with various investment opportunities. Proper interpretation of this metric allows for a better alignment of investment choices with individual risk profiles and investment objectives.
Interpreting the Standard Deviation: What Does It Really Tell You?
The standard deviation of the returns provides a quantifiable measure of investment risk. A higher standard deviation indicates greater price fluctuations and, consequently, higher risk. Conversely, a lower standard deviation suggests more stable returns and lower risk. Investors can use this metric to compare the relative risk of different investments. For instance, a high-growth stock with a high standard deviation might be suitable for an aggressive investor with a long time horizon, while a low-volatility bond with a low standard deviation would be more appropriate for a conservative investor seeking capital preservation. The standard deviation of the returns is a critical tool for understanding and managing risk within an investment portfolio.
Understanding the standard deviation’s implications allows for informed decision-making. Consider two investments: one with a standard deviation of 10% and another with a standard deviation of 2%. The investment with the 10% standard deviation exhibits significantly greater price swings. While it might offer higher potential returns, it also carries substantially higher risk of significant losses. The 2% standard deviation investment, on the other hand, suggests greater stability. This information is crucial when aligning investment choices with individual risk tolerance and financial objectives. The standard deviation of the returns serves as a key indicator of an investment’s volatility and potential for loss.
Different investors will interpret the standard deviation differently based on their individual circumstances and risk profiles. A younger investor with a longer time horizon might be more comfortable with a higher standard deviation, accepting greater volatility in pursuit of higher long-term returns. Conversely, an investor closer to retirement might prioritize capital preservation and prefer investments with a lower standard deviation, even if it means accepting lower returns. Ultimately, the standard deviation of the returns is just one piece of the investment puzzle, but it provides crucial information for making informed decisions about risk and return.
Standard Deviation vs. Other Risk Measures: A Comparative Analysis
Standard deviation of the returns quantifies the dispersion of returns around the average. Variance, its square, also measures dispersion but is less interpretable since it’s not in the same units as the returns. While standard deviation focuses solely on the historical volatility of an asset, beta measures the sensitivity of an asset’s returns to the market’s movements. A beta of 1 indicates that the asset moves in line with the market, while a beta greater than 1 suggests higher volatility than the market. Beta helps assess systematic risk, which standard deviation alone doesn’t capture.
The Sharpe ratio, a widely used risk-adjusted return measure, incorporates the risk-free rate of return. It calculates the excess return per unit of risk, offering a more holistic view of investment performance. Unlike standard deviation of the returns, which solely focuses on volatility, the Sharpe ratio considers both return and risk simultaneously. Investors often prefer investments with higher Sharpe ratios, indicating better risk-adjusted returns. Each measure has its strengths: standard deviation for understanding historical volatility, beta for systematic risk exposure, and Sharpe ratio for risk-adjusted performance assessment. The best measure depends on the specific investment context and the investor’s goals.
Understanding the nuances of these measures is crucial. For example, a high standard deviation doesn’t automatically imply a bad investment. High-growth stocks often exhibit high standard deviations but can deliver substantial returns over the long term. Conversely, a low standard deviation might suggest stability, but it could also indicate limited growth potential. Investors need to consider all risk metrics alongside their investment timeline and risk tolerance. Careful analysis of standard deviation of the returns, alongside beta and the Sharpe ratio, allows investors to make more informed decisions, aligning their portfolios with their objectives.
Using Standard Deviation in Portfolio Diversification
Portfolio diversification is a crucial strategy for managing investment risk. Investors can use the standard deviation of returns to effectively diversify their portfolios. Understanding the standard deviation of individual assets is the first step. This measure quantifies the volatility of each investment. A diversified portfolio aims to reduce overall portfolio volatility, thereby lowering the standard deviation of the returns.
The concept of correlation plays a vital role in portfolio diversification. Correlation measures the relationship between the returns of different assets. Assets with low or negative correlation tend to move in opposite directions. Including assets with low correlation in a portfolio can significantly reduce the overall portfolio standard deviation. This is because when one asset performs poorly, another may perform well, thus offsetting losses and stabilizing returns. By carefully selecting assets with low correlation, investors can construct a portfolio with a lower standard deviation of the returns than a portfolio of similarly performing assets with high correlation. This process minimizes the impact of individual asset fluctuations on the overall portfolio performance.
For example, a portfolio heavily weighted in stocks might have a high standard deviation. Adding bonds, which typically have a lower standard deviation and a low correlation with stocks, can reduce the overall portfolio’s standard deviation. Similarly, including real estate, which often exhibits low correlation with both stocks and bonds, can further stabilize the portfolio and lower the standard deviation of the returns. The goal is to achieve a desirable level of risk based on individual investment goals, all while monitoring the standard deviation to ensure that risk remains within acceptable limits. This careful asset allocation and monitoring of the standard deviation of returns is key to effective portfolio management and risk reduction.
Standard Deviation and Investment Goals: Aligning Risk with Objectives
Understanding an investment’s standard deviation of the returns is crucial, but its interpretation depends heavily on an investor’s risk tolerance and investment goals. Risk tolerance reflects an individual’s comfort level with potential losses. A conservative investor with low risk tolerance will view a high standard deviation of the returns negatively, preferring investments with more stable, albeit potentially lower, returns. Conversely, an aggressive investor with a higher risk tolerance might embrace higher standard deviations of the returns, seeking potentially greater returns despite the increased volatility.
Investment goals also significantly impact how one interprets the standard deviation of the returns. Short-term investors, focused on immediate gains, might be more sensitive to short-term fluctuations. A high standard deviation of the returns in the short term could be a significant concern. Long-term investors, however, can often weather short-term volatility. They may focus more on the long-term average return, accepting higher standard deviation of the returns as a trade-off for potentially higher overall returns. The investment time horizon directly affects the relevance of standard deviation; short-term volatility becomes less critical over longer timeframes. The standard deviation of the returns should always be considered in the context of the investor’s overall financial plan and time horizon.
Ultimately, the standard deviation of the returns serves as a vital tool for aligning investment risk with personal objectives. Investors should carefully consider their risk tolerance, investment time horizon, and financial goals when evaluating the significance of a particular standard deviation. By understanding this relationship, investors can make more informed decisions, selecting investments that appropriately balance their risk tolerance and their desired return profile. This thoughtful consideration allows for a more effective and personally suitable investment strategy, promoting long-term financial success. The standard deviation of the returns is not merely a statistical measure; it’s a key element in a personalized approach to investing.
Real-World Examples: Analyzing Standard Deviation in Specific Investments
Analyzing the standard deviation of the returns for different asset classes offers valuable insights into their risk profiles. Consider the historical performance of a broad U.S. stock market index fund. One might find a standard deviation of the returns around 15-20%. This indicates significant volatility, typical of stocks. Conversely, a long-term U.S. Treasury bond fund might exhibit a standard deviation of the returns closer to 5-10%. This lower standard deviation reflects bonds’ generally lower volatility compared to stocks. Understanding these differences is crucial for portfolio construction.
Let’s examine specific investment vehicles. A growth-oriented mutual fund, heavily invested in technology stocks, will likely display a higher standard deviation of the returns than a more conservative, income-focused mutual fund primarily holding bonds and dividend-paying stocks. The growth fund’s higher standard deviation reflects its potential for greater returns but also significantly higher risk. The calculation of the standard deviation of the returns for each fund, using historical data, reveals this risk difference clearly. Investors can use this information to align their investments with their individual risk tolerance.
Furthermore, comparing the standard deviation of returns for different exchange-traded funds (ETFs) tracking various sectors offers another practical application. An ETF focused on a volatile sector like biotechnology will generally show a higher standard deviation than an ETF tracking a more stable sector like consumer staples. By analyzing the standard deviation of the returns of various ETFs, investors can construct portfolios that balance risk and reward according to their specific objectives. The standard deviation of the returns serves as a key metric in this process, offering a quantitative measure of the inherent risk in each investment choice. This allows for a more informed and nuanced approach to portfolio management.