Suppose There Is a Simple Index of Two Stocks

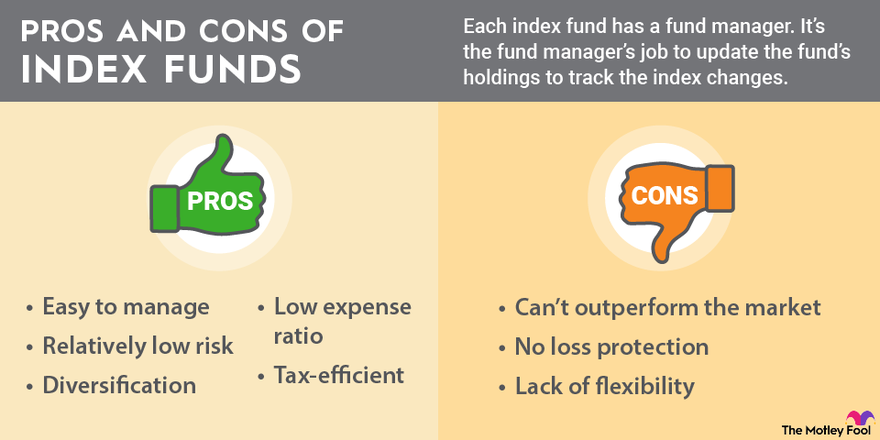
Understanding Market Movements: A Simplified Stock Index Example

The stock market index is a vital tool for investors. It provides a snapshot of the overall performance of a specific group of stocks. Think of it as a report card for a segment of the market. Instead of tracking hundreds or thousands of individual stocks, investors can monitor a single index value to gauge the general direction of the market. This simplified view helps in understanding broader market trends and making informed investment decisions. To grasp the core principles, it is helpful to consider this question: suppose there is a simple index of two stocks? Understanding how such a basic index is constructed and behaves provides a solid foundation for comprehending the complexities of more sophisticated market indicators. The following sections will guide you through the process of calculating a simple two-stock index, step by step.

This “How to” guide emerges organically from the topic of understanding market movements. Market indices encapsulate the movements of multiple stocks. Therefore, understanding index construction provides direct insight into how the market, or a segment of it, is performing. This guide addresses the practical application of calculating an index. It uses a simplified example to illustrate the underlying principles. In reality, most indices contain many stocks and employ complex weighting schemes. However, by starting with a manageable example, the fundamental concepts become much clearer. Many investors consider, suppose there is a simple index of two stocks, how does one calculate the index value? This is the question this guide will answer.

Calculating a two-stock index offers a valuable learning experience. It allows you to understand the core mechanics of index construction without the complexities of large datasets and intricate formulas. This simplified approach is perfect for beginners who are looking to demystify market movements and develop a better understanding of how indices are used to track and interpret market performance. The knowledge gained from this example can then be applied to understanding more complex indices and making informed investment decisions. The calculation of an index, especially considering the question, suppose there is a simple index of two stocks, is the first step in becoming proficient in understanding how the market works.

Defining the Stocks and Initial Values

To create a basic two-stock index, the first step involves selecting the stocks that will constitute the index. For illustrative purposes, suppose there is a simple index of two stocks: “TechGiant,” representing a technology company, and “EnergyCorp,” representing an energy company. These are hypothetical examples chosen to represent different sectors of the market. Once the stocks are selected, their initial prices need to be established. Let’s say TechGiant’s initial price is $100 per share, and EnergyCorp’s initial price is $50 per share. The index’s base value also needs to be determined. This base value serves as the starting point for tracking the index’s performance over time. A common base value is 100, but any number can be used. Suppose there is a simple index of two stocks, a base value of 100 will be used in this example.

The next step is to consider how the index will be weighted. A simple approach is to use a price-weighted method, where the index value is calculated based on the sum of the stock prices. Alternatively, a market-capitalization-weighted method can be used, where each stock’s weight in the index is proportional to its market capitalization (stock price multiplied by the number of outstanding shares). For simplicity, let’s assume this index is price-weighted. This means that TechGiant, with its higher initial price, will have a greater influence on the index value than EnergyCorp initially. The initial index value would then be calculated by summing the initial stock prices ($100 + $50 = $150) and then adjusting this sum to match the desired base value of 100. This adjustment involves a divisor, which is calculated by dividing the sum of the initial stock prices ($150) by the base value (100). The divisor in this case is 1.5. Therefore, suppose there is a simple index of two stocks, the initial calculation is crucial for future performance tracking.

With the initial values and divisor established, the index is ready to track market movements. It’s important to remember that this simple two-stock index is not intended to be representative of the entire market. It serves as a tool to illustrate the basic principles of index construction. Furthermore, the concept of market capitalization plays a role in understanding the relative size and influence of each company within the broader market, even though in our simplified model we may be using a price weighted approach. For example, even though it is a simplified model, suppose there is a simple index of two stocks where one has a significantly higher market cap. This is why broader market indices typically use market-capitalization weighting to better reflect overall market performance.

Calculating the Index Value Over Time

To illustrate how an index functions, suppose there is a simple index of two stocks. The index value is calculated based on a specific formula, which can be price-weighted or market-capitalization-weighted. For simplicity, let’s consider a price-weighted approach. This means the index value is directly influenced by the prices of the stocks included.

Suppose there is a simple index of two stocks, “TechGiant” and “EnergyCorp.” Assume at Time 0 (the base period), TechGiant’s price is $50 and EnergyCorp’s price is $100. The initial index value is set at 100. To calculate the index value at Time 1, suppose TechGiant’s price increases to $55 and EnergyCorp’s price decreases to $95. A simple price-weighted calculation would involve summing the new prices ($55 + $95 = $150) and comparing it to the initial sum of prices ($50 + $100 = $150). To reflect changes relative to the base value, a divisor is introduced. The initial divisor is calculated as the initial sum of prices ($150) divided by the initial index value (100), resulting in a divisor of 1.5. Therefore, the index value at Time 1 is the new sum of prices ($150) divided by the divisor (1.5), which equals 100.

Now, consider Time 2. Suppose there is a simple index of two stocks. TechGiant’s price rises further to $60, and EnergyCorp’s price remains at $95. The new sum of prices is $60 + $95 = $155. The index value at Time 2 is $155 / 1.5 = 103.33. This indicates a 3.33% increase from the base value. Finally, at Time 3, suppose TechGiant’s price drops to $58, and EnergyCorp’s price increases to $105. The sum becomes $58 + $105 = $163. The index value is now $163 / 1.5 = 108.67. These examples demonstrate how fluctuations in individual stock prices impact the overall index value, providing a snapshot of the combined performance of the selected stocks.
Suppose there is a simple index of two stocks and this calculation shows the fluctuation.

Addressing Stock Splits and Dividends

Corporate actions, such as stock splits and dividends, can significantly impact index calculations. To ensure the index remains a consistent and accurate reflection of the underlying stock performance, adjustments are necessary. These adjustments primarily affect the divisor used in the index calculation. Suppose there is a simple index of two stocks, TechGiant and EnergyCorp. Consider how a stock split in TechGiant would affect our index value. Without adjustment, the index would appear to drop significantly, even though the actual market capitalization of TechGiant remains the same.

A stock split increases the number of outstanding shares while decreasing the price per share proportionally. To maintain the index’s continuity, the divisor is adjusted so that the index value remains unchanged immediately after the split. The new divisor is calculated to offset the price change caused by the split. Similarly, dividends, particularly large or special dividends, can also distort the index. When a company pays a dividend, its stock price typically decreases by the dividend amount. Again, the divisor needs adjustment to reflect this change accurately. Suppose there is a simple index of two stocks, and EnergyCorp issues a substantial dividend; the divisor is modified to prevent a misleading drop in the index value.

The adjustment process involves recalculating the divisor based on the new stock prices after the split or dividend distribution. The formula ensures that the index level is the same before and after the corporate action. This recalculated divisor is then used for all subsequent index calculations until another corporate action necessitates a further adjustment. Accurate divisor adjustments are crucial. They guarantee that the index reflects genuine market movements rather than artificial fluctuations caused by corporate actions. Suppose there is a simple index of two stocks; understanding how these adjustments are made is vital for interpreting index performance accurately. The goal is to isolate the impact of actual trading activity from the effects of corporate events, providing a clearer picture of the overall market trend.

Analyzing Index Performance: Percentage Changes and Trends

Interpreting the movements of an index is crucial for understanding market dynamics. This involves analyzing percentage changes from the base value and identifying trends over time. Suppose there is a simple index of two stocks. The percentage change provides a clear indication of the index’s performance relative to its starting point. For example, if the index starts at a base value of 100 and rises to 110, it represents a 10% increase. This increase suggests that, on average, the two stocks within the index have appreciated in value.

To calculate the percentage change, the following formula is used: [(Current Index Value – Base Index Value) / Base Index Value] * 100. By applying this formula at different time intervals, investors can track the index’s performance and identify trends. An upward trend indicates positive performance of the included stocks, while a downward trend suggests negative performance. Suppose there is a simple index of two stocks, its movements can be visually represented using a chart. The chart could plot the index value over time, making it easier to identify patterns and trends. Visualizing the data helps investors quickly grasp the overall performance of the stocks represented by the index.

Consider a scenario where “TechGiant” experiences substantial growth, while “EnergyCorp” remains relatively stable. This disparity would influence the index’s overall performance. Analyzing the index’s movements alongside individual stock performance offers valuable insights. It’s important to remember that this simple index is a tool for illustrative purposes. Suppose there is a simple index of two stocks; its changes reflect the combined performance of the selected components. The index’s performance serves as a basic indicator, but it should be considered within the context of broader market analysis and individual company fundamentals. Understanding these changes provides a foundational understanding of how broader market indexes function and how they reflect overall market sentiment.

Limitations of a Two-Stock Index

While a two-stock index provides a simplified illustration of index construction, it is crucial to acknowledge its inherent limitations. A primary drawback is its lack of representativeness.
Suppose there is a simple index of two stocks; it cannot accurately reflect the overall market’s performance. The broader market comprises numerous sectors and companies, each contributing uniquely to the economy. An index based on just two stocks is highly susceptible to the individual performance of those specific companies, making it a poor indicator of broader market trends.

Consider, for example, that “TechGiant” experiences a significant technological breakthrough, leading to a surge in its stock price. This would disproportionately inflate the two-stock index, potentially giving a misleading impression of overall market health. Conversely, if “EnergyCorp” faces regulatory challenges, causing its stock price to plummet, the index would reflect this decline, even if other sectors are performing well. This sensitivity to individual company performance makes the two-stock index unreliable for making broad investment decisions or gauging the true state of the market. Suppose there is a simple index of two stocks behaving erratically; that index offers a skewed perspective.

In contrast, broader market indexes like the S&P 500 or the Dow Jones Industrial Average encompass a diverse range of companies across various sectors. This diversification mitigates the impact of individual stock fluctuations, providing a more balanced and representative view of market performance. The S&P 500, for instance, tracks the performance of 500 of the largest publicly traded companies in the United States, offering a significantly more comprehensive snapshot of the economy. Therefore, a two-stock index serves primarily as an educational tool to understand index mechanics, not as a reliable indicator for real-world investment strategies. Suppose there is a simple index of two stocks; its limited scope restricts its practical application beyond illustrative purposes.

Expanding the Index: Adding More Stocks

The illustrative example presented previously, suppose there is a simple index of two stocks, serves as a foundational understanding. To create a more representative picture of the market, an index can be expanded to include a larger number of stocks. This expansion introduces complexities but also significantly increases the index’s ability to reflect broader market trends. A two-stock index, while useful for grasping the core mechanics, is inherently limited in its scope and susceptible to the specific performance of those two companies. A wider range of stocks provides diversification and reduces the impact of any single company’s movements.

When scaling up the index, several factors must be considered. One crucial element is the weighting methodology. In the two-stock example, a simple price-weighted or market-cap-weighted approach may suffice. However, with more stocks, more sophisticated weighting schemes might be necessary. These could include equal weighting, fundamental weighting (based on factors like revenue or earnings), or variations of market-cap weighting. Each method has its own advantages and disadvantages, impacting the index’s sensitivity to different market segments. For instance, a suppose there is a simple index of two stocks, where one has extraordinary growth could skew the overall results more than in an equal-weighted index. The selection of stocks to include also becomes more critical; careful consideration must be given to industry representation, liquidity, and overall market relevance.

Another complexity that arises with a larger index is the need for periodic rebalancing. Rebalancing involves adjusting the weights of the constituent stocks to maintain the desired weighting scheme. This is essential because stock prices constantly fluctuate, causing the original weights to drift over time. For example, if one stock in the index significantly outperforms others, its weight will increase relative to the others, potentially distorting the index’s intended representation. Rebalancing ensures that the index continues to accurately reflect the desired market segment or investment strategy. Suppose there is a simple index of two stocks, which would not require constant rebalancing. However, in a broader index with hundreds of stocks, regular rebalancing becomes a necessity. This process often involves selling some of the overweighted stocks and buying some of the underweighted stocks. These complexities, while adding to the administrative burden, are crucial for maintaining the integrity and representativeness of a diversified stock market index.

Practical Applications of Understanding Simple Indexes

Understanding the construction of simple indexes, even one like a two-stock index, provides tangible benefits for investors. It demystifies the complex world of market indicators, revealing the underlying mechanics that drive index movements. This knowledge empowers investors to move beyond simply following the numbers and instead, understand the “why” behind market fluctuations. Suppose there is a simple index of two stocks; grasping its calculation equips you to interpret broader market indexes with greater insight.

Specifically, understanding a simple index enhances an investor’s ability to assess risk and return. By dissecting how individual stock prices influence the index value, investors gain a clearer picture of the potential impact of individual holdings on overall portfolio performance. This understanding is particularly valuable when analyzing sector-specific indexes or thematic ETFs, where the performance of a smaller group of stocks significantly impacts the fund’s returns. Suppose there is a simple index of two stocks, an investor can extrapolate these principles to understand the impact of the top holdings in larger, more complex indexes. This knowledge allows for more informed decisions about diversification and asset allocation.

Furthermore, understanding simple indexes promotes critical thinking about investment strategies. It encourages investors to question the methodologies behind different indexes and recognize their inherent biases or limitations. For example, a price-weighted index will be more heavily influenced by higher-priced stocks, regardless of their market capitalization. Recognizing this can lead to a more nuanced understanding of market trends and prevent investors from blindly following index-based investment products. Suppose there is a simple index of two stocks; understanding its construction is a stepping stone to understanding the subtleties of more advanced weighting schemes, like market-cap weighting or fundamental indexing. Ultimately, this understanding fosters a more informed and discerning approach to investing, leading to better long-term outcomes. The simplicity of a two-stock index provides a safe space to experiment with calculations and analysis, without the overwhelming complexity of real-world market data. The investor can learn in a more controlled environment.