How to Calculate Delta of an Option

Understanding Option Delta: The Basics

Option delta represents a crucial concept in options trading. It quantifies the sensitivity of an option’s price to changes in the underlying asset’s price. Specifically, the delta indicates how much an option’s price is expected to move for every one-dollar change in the price of the underlying asset. Understanding how to calculate delta of an option is vital for effective risk management.

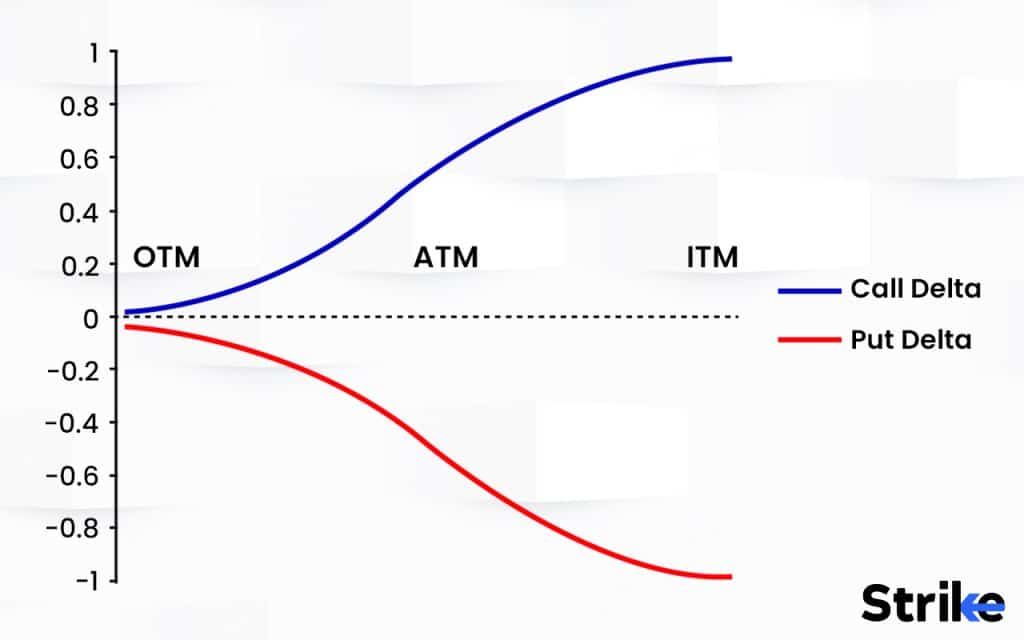
The delta value ranges from 0 to 1 for call options and from -1 to 0 for put options. A call option with a delta of 0.7, for example, is expected to increase by $0.70 for every $1 increase in the underlying asset’s price. Conversely, a put option with a delta of -0.5 is expected to decrease by $0.50 for every $1 increase in the underlying asset’s price (or increase by $0.50 for every $1 decrease in the underlying asset’s price). The absolute value of the delta indicates the magnitude of the price change. Knowing how to calculate delta of an option helps traders gauge potential profits and losses.

The delta plays a significant role in hedging and risk management strategies. Traders use delta to construct portfolios that are neutral to small price movements in the underlying asset, a technique known as delta hedging. By understanding an option’s delta, traders can effectively manage their exposure to market fluctuations and mitigate potential losses. Furthermore, the delta provides valuable insights into the probability of an option expiring in the money. An option with a higher delta is more likely to be in the money at expiration than one with a lower delta. Mastering how to calculate delta of an option is thus essential for any options trader seeking to optimize their trading strategies and manage risk effectively.

Factors Influencing Option Delta

Several factors influence how to calculate delta of an option. The current price of the underlying asset plays a crucial role. As the asset price increases, the delta of a call option increases, approaching 1 for in-the-money calls. Conversely, the delta of a put option decreases, approaching -1 for in-the-money puts. The strike price also significantly impacts delta. Options closer to being at-the-money have higher delta sensitivity.

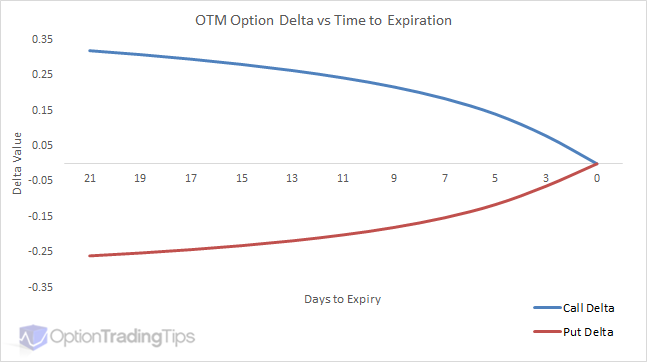
Time until expiration is another key determinant. As the expiration date nears, the delta of an option tends to move closer to either 0 or 1 (or -1 for puts), depending on whether the option is out-of-the-money or in-the-money. The volatility of the underlying asset also affects delta. Higher volatility generally increases the delta of at-the-money options, making them more sensitive to price changes in the underlying asset. This is because increased volatility raises the probability of the option ending up in the money. Understanding how to calculate delta of an option requires appreciating the impact of volatility.

Finally, the risk-free interest rate has a minor influence on option delta. While its effect is less pronounced than other factors, a higher risk-free rate generally leads to a slightly higher delta for call options and a slightly lower delta for put options. It’s vital to consider all these elements to understand how to calculate delta of an option and its behavior. By grasping how each factor impacts delta, traders can better assess option risk and make informed decisions. The interplay of these factors dictates the sensitivity of an option’s price to changes in the underlying asset.

How to Determine Option Delta: Methods and Approaches

Several methods exist for determining the delta of an option. Understanding these approaches is crucial for traders seeking to effectively manage risk and implement various trading strategies. While precise calculation can be complex, several tools and techniques can provide accurate estimates of an option’s delta.

One theoretical approach involves using the Black-Scholes model. This model is a mathematical equation that considers several factors. These factors include the underlying asset’s price, the option’s strike price, time to expiration, volatility, and the risk-free interest rate. The Black-Scholes model provides a theoretical delta value. However, it’s important to note that the Black-Scholes model relies on several assumptions. These assumptions, such as constant volatility and efficient markets, may not always hold true in real-world trading scenarios. Therefore, relying solely on the Black-Scholes model might not always provide the most accurate delta estimate. This is an important consideration regarding how to calculate delta of an option in practical scenarios.

Real-world methods offer a more practical approach to determining option delta. A common method involves using option chains provided by brokers and exchanges. Most brokers provide option chains that include delta values for each option contract. For example, brokers such as Interactive Brokers and TD Ameritrade provide comprehensive option chains with readily available delta information. These option chains are updated in real-time, reflecting current market conditions. By accessing these option chains, traders can quickly determine the delta of a specific option contract. Understanding how to calculate delta of an option using these tools is essential for active trading and risk management. Moreover, some financial websites also provide option chain data, allowing traders to access delta information from various sources. It’s important to compare delta values from different sources to ensure accuracy. This is due to slight variations in calculation methodologies or data updates. This practical method simplifies the process of determining option delta. This makes it accessible to both novice and experienced option traders, offering a reliable way on how to calculate delta of an option.

Calculating Delta Using Option Chains

To effectively understand how to calculate delta of an option, one must know how to interpret option chains. Option chains, readily available from brokers and exchanges, provide a wealth of information. This includes the delta for each option contract. Locating the delta value is typically straightforward. Most option chains display delta in a dedicated column. The column is often labeled “Delta” or represented by the Greek symbol “Δ”. The value presented is usually a decimal number between 0 and 1 for call options. It ranges between -1 and 0 for put options. These values represent how the option price is expected to change for every $1 move in the underlying asset’s price. For example, if a call option has a delta of 0.60, the option’s price should theoretically increase by $0.60 for every $1 increase in the underlying asset’s price, assuming all other factors remain constant. Understanding how to calculate delta of an option with this method is crucial for effective risk management.

The units of delta displayed on an option chain can sometimes be expressed as a percentage. For instance, a delta of 0.50 might be shown as 50%. It’s important to verify how the broker or exchange presents the delta value to avoid misinterpretations. To further clarify, consider a hypothetical example. An option chain for a stock trading at $100 shows a call option with a strike price of $105 and a delta of 0.30. This indicates that if the stock price rises to $101, the call option’s price is expected to increase by approximately $0.30. Conversely, a put option with a strike price of $95 and a delta of -0.40 suggests that if the stock price decreases to $99, the put option’s price should increase by roughly $0.40. The negative sign for puts indicates an inverse relationship between the underlying asset’s price and the option’s price. Understanding how to calculate delta of an option using real-time market data is a key skill for options traders.

Many online brokers provide comprehensive option chain data. Interactive Brokers and TD Ameritrade are examples of platforms that offer detailed option information, including delta values. These platforms often allow users to customize the display. Users can add or remove columns, filter options based on specific criteria, and analyze option chains in various ways. When examining an option chain, pay close attention to the expiration date and strike price of each option. Also consider the bid-ask spread, which can affect the accuracy of the delta value. Liquid options with narrow spreads tend to have more reliable delta values. In conclusion, learning how to calculate delta of an option and interpret it from option chains is an essential skill for anyone involved in options trading. It helps traders assess risk, manage positions, and implement various trading strategies.

The Delta Approximation Formula

One straightforward method to understand how to calculate delta of an option involves using an approximation formula. This formula offers a practical way to estimate delta, especially when precise values from option chains or complex models are unavailable. The delta approximation formula is: Delta ≈ Change in Option Price / Change in Underlying Price. This formula suggests that the delta is approximately equal to the change in the option’s price divided by the change in the underlying asset’s price. It’s crucial to recognize that this approximation is most accurate for small, incremental movements in the underlying asset’s price. Larger price swings can reduce the accuracy of this calculation, as delta itself changes with price fluctuations. Understanding how to calculate delta of an option using this approximation provides a quick and intuitive sense of an option’s sensitivity.

To illustrate how to calculate delta of an option using this approximation, consider a hypothetical example. Suppose a call option’s price increases by $0.50 when the underlying stock price increases by $1.00. Using the formula, the approximate delta would be: Delta ≈ $0.50 / $1.00 = 0.50. This indicates that for every $1 increase in the stock price, the option price is expected to increase by approximately $0.50. Conversely, if the stock price decreases by $1, the option price should decrease by roughly $0.50. This simplified calculation method of how to calculate delta of an option helps traders quickly assess the potential impact of price changes on their option positions. However, it’s important to remember that this is an approximation, and the actual delta may vary due to other factors.

Keep in mind that while the delta approximation formula provides a useful estimate, it has limitations. The accuracy of this method decreases as the price change of the underlying asset becomes more substantial. Moreover, factors like time decay (theta) and changes in volatility (vega) are not accounted for in this simplified calculation, yet they do influence the real delta of the option. Therefore, while this formula is a handy tool for quick estimations, it should be used with caution and supplemented with more precise delta values from option chains or other models, especially when managing significant option positions or implementing complex trading strategies. Knowing how to calculate delta of an option using multiple methods allows for more informed decision-making in option trading.

Delta Hedging: Managing Option Risk

Delta hedging is a strategy employed to reduce the risk associated with options trading. It involves creating a portfolio that is neutral to small price movements in the underlying asset. The goal is to offset potential losses in an option position with gains in the underlying asset, or vice versa. Understanding how to calculate delta of an option is essential for implementing an effective delta hedge. Since, by definition, delta measures the sensitivity of the option price to changes in the underlying asset’s price, it becomes a critical factor in determining the hedge ratio. This involves using offsetting positions to balance the impact of delta on your overall portfolio.

Here’s how delta hedging works in practice. Imagine a trader sells a call option. Because a short call option has a negative delta, if the underlying asset’s price increases, the call option will increase in value, resulting in a loss for the trader. To hedge this risk, the trader can purchase shares of the underlying stock. The number of shares to buy is determined by the option’s delta. For example, if the short call option has a delta of 0.40, the trader would buy 40 shares of the underlying stock for each call option sold (assuming each option represents 100 shares). This creates a position that is approximately delta-neutral, meaning that small changes in the underlying asset’s price will have a minimal impact on the overall portfolio value.

The portfolio is not perfectly hedged in practice and may require dynamic adjustments. The trader must continuously monitor and adjust the hedge as the option’s delta changes. This is because delta is not static. It changes as the underlying asset’s price fluctuates, time passes, and volatility shifts. These adjustments, known as rebalancing, are crucial to maintaining a delta-neutral position and managing risk effectively. Rebalancing might involve buying or selling shares of the underlying asset to maintain the desired hedge ratio based on the new delta. This dynamic approach helps traders mitigate the risk associated with writing or holding option positions, since understanding how to calculate delta of an option and employing delta hedging can significantly improve risk management in options trading.

Limitations of Delta and Considerations for Practical Application

Delta serves as a valuable tool for gauging option sensitivity, but it possesses inherent limitations. Understanding these limitations is crucial for the effective application of delta in trading and risk management. It’s important to recognize that delta is not a static measure; it fluctuates in response to changes in the underlying asset’s price, time remaining until expiration, and other factors. The dynamic nature of delta necessitates continuous monitoring and adjustments to hedging strategies. To understand how to calculate delta of an option is important, but the user must know the limitations for the most accurate use.

One key consideration is the concept of “gamma.” Gamma measures the rate of change of delta with respect to changes in the underlying asset’s price. A high gamma indicates that delta is highly sensitive to price movements, while a low gamma suggests that delta is more stable. Traders must be aware of gamma when employing delta-hedging strategies, as it can impact the effectiveness of the hedge. Furthermore, changes in volatility can significantly affect delta estimates. An increase in implied volatility typically increases the delta of out-of-the-money options and decreases the delta of in-the-money options. Therefore, it is important to consider volatility when determining how to calculate delta of an option and interpreting its meaning.

In practical application, relying solely on delta can be misleading. It’s essential to consider other factors, such as gamma, vega (sensitivity to volatility), and theta (time decay), to gain a more comprehensive understanding of option risk. Moreover, the accuracy of delta calculations depends on the accuracy of the underlying assumptions, such as the volatility estimate. In real-world markets, these assumptions may not always hold true. When considering how to calculate delta of an option, it’s imperative to remember that delta is an approximation, not a precise measurement. While it is a vital tool in managing option risk, it should not be used in isolation. Combining delta with other risk measures and incorporating market experience can lead to more informed and effective trading decisions.

Practical Examples of Delta in Trading Strategies

Context_8: Traders employ delta in various option trading strategies to manage risk and speculate on price movements. Understanding how to calculate delta of an option is crucial for these strategies. One common application is delta hedging, where traders aim to create a portfolio that is insensitive to small changes in the underlying asset‘s price. For example, a trader who sells a call option (expecting the price to stay below the strike price) takes on negative delta exposure. To offset this, the trader buys shares of the underlying stock. The number of shares purchased is typically equal to the absolute value of the option’s delta multiplied by the number of options contracts sold, and multiplied by 100 (since one option contract controls 100 shares). This strategy seeks to neutralize the portfolio’s sensitivity to price changes, but needs to be re-evaluated periodically.

Another use of delta is in directional trading. Traders who are bullish on an asset might buy call options with high delta values. A call option with a delta of 0.8, for instance, will increase in value by approximately $0.80 for every $1 increase in the underlying asset’s price (times 100 since each contract represents 100 shares). This provides leveraged exposure to the underlying asset. Conversely, bearish traders could purchase put options with a delta close to -1 to profit from a decrease in the underlying’s price. Knowing how to calculate delta of an option enables traders to estimate potential gains or losses based on anticipated price movements. However, changes in volatility and the passage of time will affect the delta, and therefore, the trader’s position.

Delta-neutral strategies combine options with different deltas to create a portfolio with an overall delta near zero. This involves simultaneously buying and selling options, or combining options with the underlying asset, to achieve a delta-neutral position. Iron condors and straddles are examples of such strategies, where the trader profits from time decay and minimal price movement in the underlying asset. While these strategies are designed to be insensitive to small price changes initially, they often require adjustments as the underlying’s price fluctuates, changing the deltas of the individual options. Therefore, understanding how to calculate delta of an option and how delta changes over time (gamma) is essential for managing these complex option positions. Remember that these are just examples, and no trading strategy guarantees profits. It is important to fully understand the risks involved before implementing any options trading strategy.